基于改进杠杆法的行星变速机构传动方案研究

许爱芬，贾巨民，刘 宁

(1.军事交通学院 军事物流系，天津300161;2.军事交通学院 国防交通系，天津300161)

杠杆法于1999 年由同济大学李庆等［1］提出，是分析行星齿轮传动方案的一种简单直观方法，应用较为广泛。李兴华、何国旗等［1-5］详细介绍了杠杆法的基本原理，并应用该方法重点对轿车主要车种通常采用的三自由度双排行星齿轮变速器传动方案进行了分析和研究，得出了可行方案的传动简图。杨啟梁［6］利用杠杆法针对双排行星齿轮变速机构，阐述了其传动方案设计过程及方法。尤明福等［7］对传统杠杆法进行了拓展，拓展后的方法主要用于分析ZF 类(拉威娜式)三排行星齿轮机构传动方案。邢庆坤等［8］基于组合杠杆法分析了二自由度和双排三自由度的行星排传动方案。

上述文献主要是利用杠杆法分析轿车上典型的并联式多行星排(主要是两排)的传动方案。而对于存在串联方式的多行星排结构，传统杠杆法就失去了作用，因为在串联方式中常有常输入元件存在。单行星排串联辛普森结构变速机构是6挡自动变速器中的典型结构。本文以该类结构为研究对象，提出“等效输入转速”的概念，改进传统杠杆法，并用改进后的杠杆法分析该类结构的传动方案，以得到可行方案的转速图。

1 杠杆法的基本原理

1.1 单行星排齿轮传动杠杆原理

单级行星排和双级行星排运动规律特性方程分别为

式中:n1、n2、n3分别为太阳轮S、齿圈R 和行星架C 的转速;α为行星排的特性参数，α=ZR/ZS，ZR、ZS分别为齿圈的齿数和太阳轮的齿数。

由式(1)和(2)可以看出，3 个元件中，任选2个分别作为输入件和输出件，另1 个作为制动件，整个轮系就以一定的传动比传递动力［9］。传动比的大小与α紧密相关，并且符合杠杆原理。因此，可以将单行星排等效为1 个垂直杠杆和3 个支点，3 个支点A、B、D分别代表太阳轮S、齿圈R 和行星架C。对于单级行星排，中间支点为行星架C，两端支点分别为太阳轮S 和齿圈R(如图1(a)所示)。对于双级行星排，中间支点为齿圈R，两端支点分别为太阳轮S 和行星架C(如图1(b)所示)。支点A和B到支点D的距离分别与齿圈的齿数ZR和太阳轮的齿数ZS成正比。

1.2 多行星排齿轮传动杠杆原理

当多个行星排由构件相互连接时，每个行星排均等效为1 个垂直杠杆和3 个支点。构件之间的连接等效为支点之间的连接(如图2 所示)，图中αi(i=1，2)为第i排行星排的特性参数，K为比例系数。

图1 单行星排齿轮传动结构简图及杠杆图

图2 多行星排齿轮传动结构简图及杠杆图

2 辛普森式行星变速机构传动方案分析

辛普森式行星变速机构的特点是前、后2 个行星排的太阳轮固联，前排齿圈和后排行星架固联(如图3 所示)，或前排行星架和后排齿圈固联［10］(如图4 所示)。

从图3(b)和图4(b)中可以看出，两行星排之间并联时，在杠杆图上有2 个重叠点，因此杠杆图上有4 个构件点，分别是输入点、输出点、制动点和连接点。将这4 个构件点进行不同的排列组合就可以得到不同的传动比。根据构件点和构件功能的选择原则［6］，可以分析出不同固联方式下的传动特性(见表1)。

图3 前排齿圈和后排行星架固联的辛普森式行星变速机构

图4 前排行星架和后排齿圈固联的辛普森式行星变速机构

表1 辛普森式行星齿轮变速机构传动特性

方案分析:

(1)3 种传动方案均可以实现1 个倒挡、2 个减速挡、1 个直接挡和1 个超速挡。

(2)各个挡位之间换挡时，只需切换1 个操纵件，换挡操纵简单。

(3)各非直接挡的传动比均可以通过改变行星排的特性参数进行调整。

(4)在方案1 和方案3 中，均出现了太阳轮(构件点D)为制动件的情况。相对比而言，方案2是较优的选择。

3 单行星排串联辛普森结构变速机构传动方案分析

3.1 单级行星排串联辛普森结构

单级行星排串联辛普森结构变速机构的典型杠杆图如图5 所示，图中，Si、Ci和Ri(i=1，2，3)分别表示第i排的太阳轮、行星架和齿圈;αi(i=1，2，3)表示第i排行星排的特性参数;ZSi(i=1，2，3)表示第i排行星排的太阳轮齿数;Ki(i=1，2，3，4，5)表示第i个换挡执行元件;ai(i=2，3)表示第i排的比例系数。

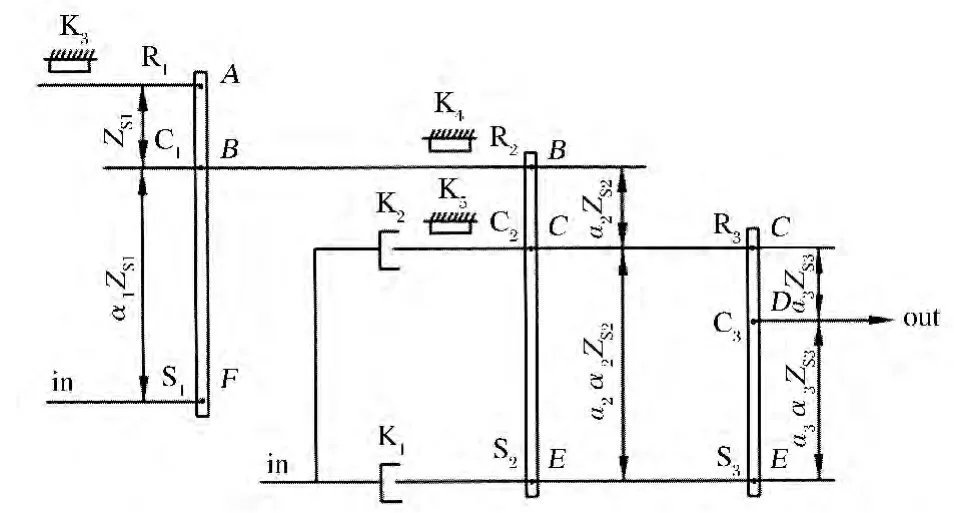
图5 单级行星排串联辛普森结构变速机构杠杆图

由于第1 行星排的太阳轮处(F点)存在常输入转速，这有悖于传统杠杆法的分析原则［7］。本文提出“等效输入转速”的概念，将传统杠杆法进行改进，得到改进的杠杆法，有效地解决了这一突出问题。具体步骤如下:

(1)确定单行星排，以常输入转速点为输入点，串联点为输出点，得到等效输入转速值。单行星排是指与其他行星排串联的行星排。在图5中，第1 排行星排为单行星排，其通过串联点B与后续并联行星排连接，且为唯一连接点;因此，B为输出点，F为输入点，A为制动点。根据单行星排杠杆图可得到1 个输出转速，作为后续并联行星排的1 个输入，这一转速就称为“等效输入转速”。

(2)将等效输入转速值标注在后续并联行星排的串联点处，删掉单行星排，得到改进的杠杆图(如图6 所示)。

图6 单级行星排串联辛普森结构的变速机构的改进杠杆图

(3)根据并联行星排的杠杆分析完成传动方案分析。图6 中，K'3是一个虚拟的离合器，表示前排的执行元件工作时所产生的等效输入转速。当K'3结合时，等效输入转速in'有效。由图6 可以看出，改进后的杠杆图为一并联式两行星排结构杠杆图。其各挡的传动情况见表2。

3.2 双级行星排串联辛普森结构

双级行星排串联辛普森结构变速机构的典型杠杆图与图5 的唯一区别是第1 排的3 个元件的支点位置不同。

改进后的杠杆图和图6 完全一致。其各挡的传动情况见表3。综上分析可知，改进杠杆法将复杂的三行星排结构简化为并联式两行星排结构，并且将单、双级行星排串联辛普森结构变速机构的杠杆图及转速图简化为一种，只是等效输入转速不同。同时，改变行星排的特性参数就可以对传动比进行调整。这使得传动方案的分析更趋简便，也体现了改进杠杆法的裨益之处。

表3 双级行星排串联辛普森结构变速机构的传动特性

4 实例验证

4.1 Allison HD4560P 自动变速器传动方案分析

HD4560P 自动变速器是美国Allison 自动变速器4000 系列的产品之一，具有大功率高扭矩的特点，适用于恶劣条件及各种复杂条件下的高效运转。它采用的是单级行星排串联辛普森结构三行星排的组合方式，可以实现6 速。其3 个行星排的特性参数分别为α1=1.71、α2=2.29、α3=3.7，分别代入表2 中的计算公式，计算得到的传动比与其官方网站发布的数据完全吻合，验证了本文所提出的改进杠杆法是正确可行的。

4.2 CX31 自动变速器传动方案分析

CX31 自动变速器是一款主要用于重卡的6挡变速器，采用的是双级行星排串联辛普森结构三行星排的组合方式。其3 个行星排的特性参数分别为α1=2.56、α2=2.83、α3=3.4，分别代入表3 中的计算公式，计算得到的传动比与其官方网站发布的数据完全吻合，验证了本文所提出的改进杠杆法是正确可行的。

5 结 论

(1)“等效输入转速”概念的提出完善了传统的杠杆图。

(2)改进的杠杆法是分析单行星排串联辛普森结构的三排行星变速机构传动方案的有效方法。

［1］ 李庆，黄宗益，李兴华. 杠杆法在行星传动方案分析中的应用［J］.同济大学学报，1999，27(5):581-586.

［2］ 李兴华，黄宗益，张承航. 三自由度行星变速器传动方案设计［J］.中国机械工程，2002，13(20):1727-1730.

［3］ 李兴华，何国旗. 等效杠杆法分析行星齿轮传动［J］. 机械设计，2004，21(1):44-45.

［4］ 李兴华，张青松，张久林. 轿车5 挡自动变速器传动方案分析［J］.同济大学学报:自然科学版，2006，34(12):1689-1693.

［5］ 何国旗，李兴华，罗智勇，等.利用等效杠杆法分析自动变速器结合元件的布置［J］.机械科学与技术，2007，26(3):332-337.

［6］ 杨啟梁.行星齿轮变速机构方案设计的杠杆分析法［J］. 湖北工业大学学报，2006，21(3):189-192.

［7］ 尤明福，李志伟，甘伟，等.基于杠杆法的8 速自动变速器传动方案的设计［J］. 中国机械工程，2012，23(23):2801-2804.

［8］ 邢庆坤，尹华兵，赵欣源，等.基于组合杠杆法的行星变速箱方案筛选研究［J］.车辆与动力技术，2013(1):29-34.

［9］ 陈家瑞. 汽车构造:下册［M］. 北京:机械工业出版社，2010:80.

［10］ 罗新闻，霍志毅.汽车自动变速器结构原理彩色图解［M］.北京:机械工业出版社，2010:15.