双精度容差关系的粗糙集拓展模型及约简

曾 玲，付 敏，何普彦

(桂林电子科技大学数学与计算科学学院，广西桂林541004)

在信息系统的多属性决策中，由于客观事物的复杂性和人类思维的模糊性，信息有时无法用具体的精确数表示，而是以区间数的形式出现，此外，由于对数据理解或获取的限制等原因，信息系统往往存在缺失的情况，尽管如此决策者仍然渴望能从这样的信息系统中找到对决策有用的信息.

经典的粗糙集理论只能处理完备信息系统，对于不完备信息系统，人们将等价关系拓宽，提出了各种拓展关系，经典的有 M.Kryszkiewcz［1］提出的容差关系、J.Stefanowki等［2］提出的非对称相似关系、王国胤［3］提出的限制容差关系等.但是，传统的粗糙集方法主要处理的是离散属性值，而在很多实际问题中，信息值往往是连续的或者以区间数的形式出现，而对于连续属性值的处理方法主要是对连续值进行离散化后采用经典的粗糙集方法处理［4］，其本质是将属性值域划分成一些离散化区间［5-6］.因此直接研究区间值信息系统上的知识获取和约简是很有必要的.对于不完备区间值信息系统的研究，文献［7］中将不完备信息系统转化为完备信息系统的方法来处理，但这种完备化方法不可避免地增加了系统新的人为的不确定性.文献［8］中讨论了基于广义优势关系粗糙集的不完备区间值信息的处理方法，并改进了分类质量的概念.文献［9］中提出了一种基于偏序关系的粗糙集拓展模型，但该模型不能用于处理区间属性值大多数相交但不具有包含关系以及含多个连续值的情形.

文中将容差关系进行拓展，提出基于相似度和相似率的双精度容差关系，并给出极大分类约简算法，最后通过实例来说明所提出模型及约简的有效可行性.

1 预备知识

定义 1.1［10］称(U，A，V，F)是一个信息系统，其中U={x1，x2，…，xn}为有限对象集，U中的每个元素xi(i≤n)称为一个对象，A={c1，c2，…，cm}为有限属性集，A中的每个元素ck(k≤m)称为一个属性.F为U与A之间的关系集，即F={fk:U→Vk(k≤m)}，其中Vk为ck(k≤m)的值域.若，则称(U，A，V，F)是区间值信息系统.而对于连续值信息系统而言，连续值可以看作特殊的区间值，其中又若存在xi∈U，ck∈A，f(xi，ck)=*(“*”表示缺失值)，则称信息系统是不完备的，否则称信息系统是完备的.

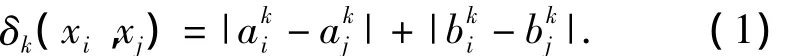
定义1.3 设(U，A，V，F)为一不完备区间值信息系统，ck∈A，xi，xj∈U，则对象xi，xj相对于属性ck的相似度定义为

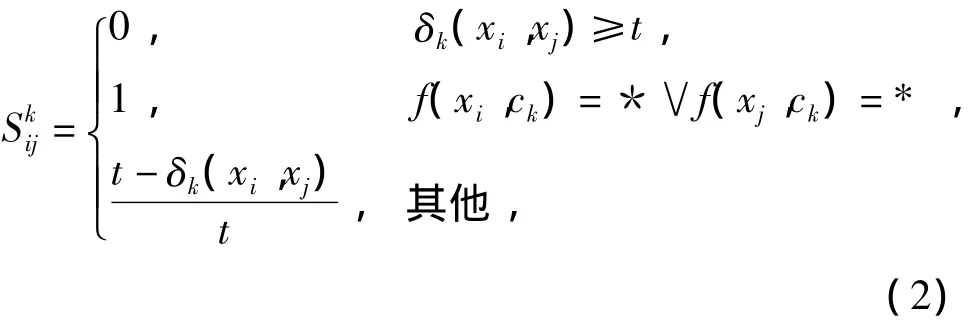
式中:δk(xi，xj)为xi，xj的相离度;t=u·max{δk(xi，xj)}，u∈［0.5，1］.

注:1)如果令t=max{δk(xi，xj)}，则只有相离度最大的两个对象间的相似度为0，而实际中，只要两个对象间的相离度大于某个值就可以认为这两个对象不能分到同一类中，相似度为0.因此参数u的设置避免了相似度不为0的范围过大，使得计算更符合实际.

2)对区间值信息系统而言，若两对象的属性值是左右两端点不相等的区间值，且两个区间相交部分为空，则两对象的相离度大于某个值就可以认为这两个对象在一定程度上是不相似的，若两对象的属性值为连续值，则两对象的相离度大于某个值就可以认为这两个对象不能分到同一类中.

3)文献［9］建立的偏序关系，对于对象的属性取值不具有包含关系且大多相交的不完备区间值信息系统以及含多个连续值的不完备区间值信息系统无能为力，此相似度的定义拓展了适用范围.

定义1.4［11］设(U，A，V，F)为一不完备区间值信息系统，B⊆A，xi，xj∈U，0 ＜ α≤1，称

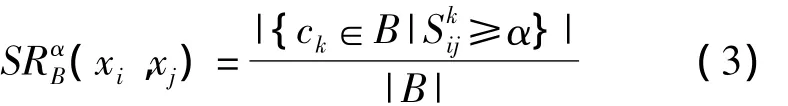
为xi，xj在属性集B下的 α - 相似率.SRαB(xi，xj)反映了在属性集B中支持xi，xj的α-相似的属性比率.

在模型求解相似类时，如果要求两对象所有属性的相似度都达到某一限度，要求过于苛刻，而相似率的引入解决了这一问题，也更符合实际.

2 双精度容差关系的粗糙集拓展模型

两个对象在同一属性下属性值之间的相似度大小，可以分为3种情况:① 两个属性值同时不为缺失值时，相似度大于或等于给定的阈值α;② 两个属性值同时不为缺失值时，相似度小于给定的阈值α;③两个属性值至少有一个为缺失值时，相似度为1.因此，在不完备区间值信息系统中，可以建立变精度容差关系将论域进行划分，而要求两对象所有属性的相似度都达到某一阈值，要求过于苛刻，因此下面又给出基于相似度和相似率的双精度容差关系.

定义2.1 对ck∈B，B⊂A，α∈(0，1］，在不完备区间值信息系统上定义如下基于相似度的容差关系:

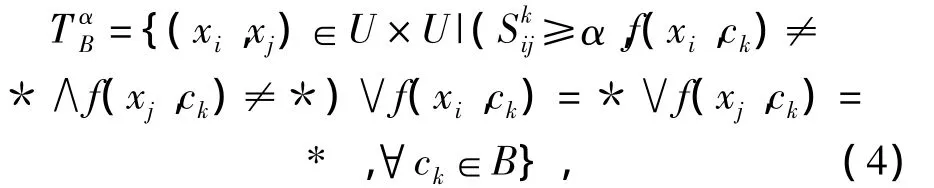
显然满足自反性，对称性，但不满足传递性.

定义2.2 设(U，A，V，F)为一不完备区间值信息系统，对ck∈B，B⊂A，α∈(0，1］，X⊆U，则X的下近似和上近似为

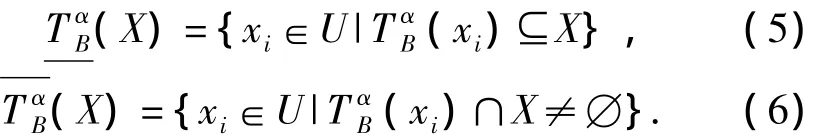
定义 2.3 对ck∈B，B⊂A，α，β∈(0，1］，α，β分别为相似度阈值和相似率阈值，在不完备区间值信息系统上定义如下双精度容差关系:

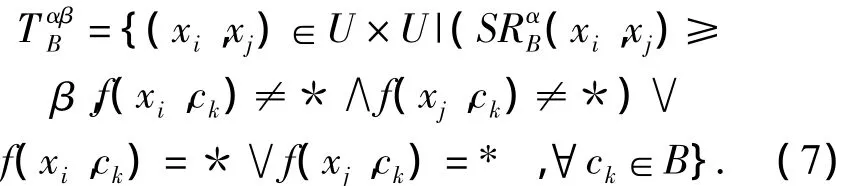
性质2.3.1 设(U，A，V，F)为一不完备区间值信息系统是如上定义的二元关系，α，β∈(0，1］，则有:

①对B⊂A，是一个容差关系，满足自反性和对称性，但不满足传递性.

② 对于参数 α，β，若满足0＜α2≤α1≤1，则有;若0＜ β2≤β1≤1，则

说明:性质2.3.1中第③点表明，在不完备区间值信息系统中，当β=1时，二元关系就退化为二元关系因此基于双精度容差关系模型是基于变精度容差关系模型的拓展.下面讨论双精度容差关系的性质.

性质2.3.2 设(U，A，V，F)为一不完备区间值信息系统是如上定义的二元关系，则有:

① 若B1⊂B2⊂A，则对 α，β∈(0，1］有

定义2.4 设(U，A，V，F)为一不完备区间值信息系统，对ck∈B，B⊂A，α，β∈(0，1］，X⊆U，则X的下近似和上近似为

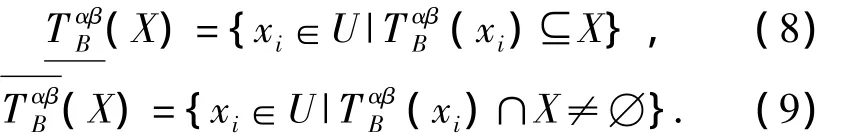
从而根据定义2.4，可得出以下定理.

定理2.1

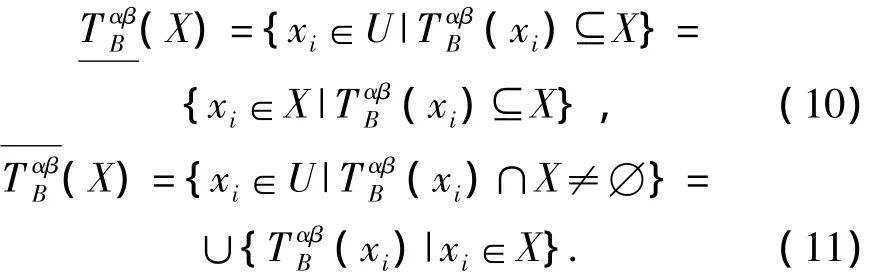
不完备区间值信息系统K=(U，A，V，F)上的双精度容差关系是自反的，因而构成论域上的一个覆盖，但一般不是等价关系，若以作为基本概念，则可能导致中所有对象虽然都与x在相似度阈值α及i相似率阈值β下关于属性B相容，但未必两两之间在相似度阈值α及相似率阈值β下关于B相容，再者可能出现的情形.因此，为解决双精度容差关系在划分论域时的不足，提高近似精度，又进一步给出了双精度极大相容类的定义.

定义2.5 设K=(U，A，V，F)是不完备区间值信息系统，α是相似度阈值，β是相似率阈值，B⊂A，M⊆N是满足其中任何两个对象关于B在双精度下都相容，则称M是一个双精度相容类;若M是一个变精度相容类，且∀xi∈U-M，∃xj∈M，使得，则称M是一个双精度极大相容类.

注:①双精度极大相容类是论域中对象满足两两相容的最大集合，任意双精度相容类必可扩展成双精度极大相容类;②双精度极大相容类是论域U中对象满足传递关系的最大子集.

容易证明双精度极大相容类满足以下性质.

性质2.5.1 设K=(U，A，V，F)是不完备区间值信息系统，α是相似度阈值，β是相似率阈值，则有:

①若B⊂A，则，都使M⊆N.

② 若B⊂A，α，γ 是相似度阈值，若 α ＜ γ，则都∃，使

③ 若B⊂A，β，γ 是相似率阈值，若 β＜γ，则，都

利用基于双精度容差关系的双精度极大相容类作为基本概念，在一定程度上克服了双精度容差关系对论域划分的不足.

记ψ(B)为属性集B所决定的所有极大相容类集，ψxi(B)为属性集B所决定的包含xi的所有极大相容类集，则 ψ(B)，ψ(B)(x∈U)分别构xii成论域U的一个覆盖，并有下列结论.

定理2.2M∈ψ(B)当且仅当

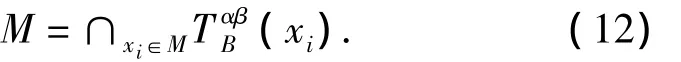
定理2.3

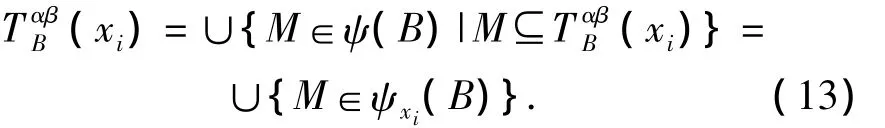
下面给出基于双精度极大相容类的下近似和上近似的定义.

定义2.6 给定不完备区间值信息系统K=(U，A，V，F)，X⊆U，则X基于双精度极大相容类的下近似和上近似为

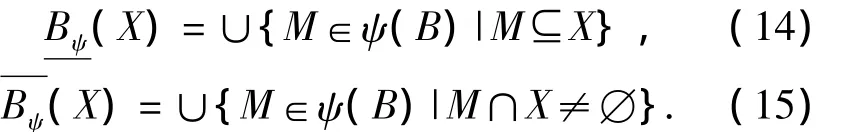
根据定理2.2，2.3，可得出定义 2.4 与定义 2.6满足如下关系:

定理2.4

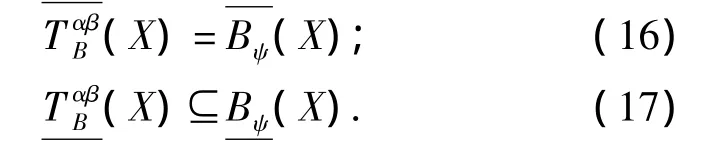
注:从定理2.2到定理2.4可以看出，基于双精度容差关系的极大相容类仍然保持文献［12］给出的关于极大相容类的一些很好的性质，提高了近似精度，拓展了粗糙集的应用范围.

3 属性约简

有了不完备区间值信息系统的双精度容差关系，就有了不完备区间值信息系统上的元知识，进一步有了ψ(B)，但确定这一知识往往xi并不需要B中所有属性，而通常只要找出B中的一个最小属性子集就能确定出知识ψxi(B)，这就是知识的属性约简，也是粗糙集理论的核心问题.通过约简可以深化对知识的认识.因此，接下来文中讨论不完备区间值信息系统基于双精度容差关系下的属性约简.

定义3.1 在不完备区间值信息系统K=(U，A，V，F)中，设 α，β∈(0，1］，B⊂A，如果MB=MA，则对∀c∈B，MB-{c}≠MB，则B是不完备区间值信息系统的一个极大分类约简.

由定义知，不完备区间值信息系统的极大分类约简就是保持双精度极大相容类分类不变的最小属性集.

定义3.2 在不完备区间值信息系统K=(U，A，V，F)中，设 α，β∈(0，1］，B⊂A，B1，B2，…，Bn是极大分类约简，如果ai∈B1∩B2∩…Bn，则ai是不完备区间值信息系统的极大分类约简的核属性.

定义3.3 在不完备区间值信息系统K=(U，A，V，F)中，α，β分别为相似度阈值和相似率阈值，对xi，xj∈U，令

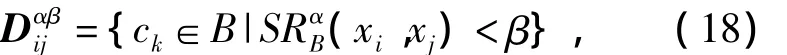
由定义可知，对任意xi，xj∈U及相似度阈值α和相似率阈值β有，即不完备区间值决策信息系统的αβ区分矩阵Dαβ是主对角线上元素全部为Ø的对称阵.

定义3.4设M是一个双精度极大相容类，称)是双精度极大相容类M的区分函数.

从而根据布尔理论，由定义3.4可得以下定理.

定理3.1B是极大双精度相容类M的约简的充要条件是∧B是M的α，β区分函数Δαβ(M)的极小析取范式中的合取式.

由以上结论可得到极大分类约简算法，算法具体步骤如下.

算法3.1 输入:不完备区间值信息系统K=(U，A，V，F)，U={x1，x2，…，xn}，A={c1，c2，…，cm}，α，β∈(0，1］.

输出:极大分类约简.

1)将决策信息表规范化，求出参数u，t，进而求出对象间的相似度.

2)给定相似度阈值α和相似率阈值β求出所有论域中对象的双精度相容类

4)根据双精度极大相容类构造区分矩阵.

5)对所有非空区分属性集进行合取，再将合取转化为析取，从而求出不完备区间值信息系统的极大相容类集的属性约简和核.

4 实例

下表1为不完备区间值决策信息系统，其属性集为A={c1，c2，c3，c4，c5，d}，对象集为U={x1，x2，…，x10}.

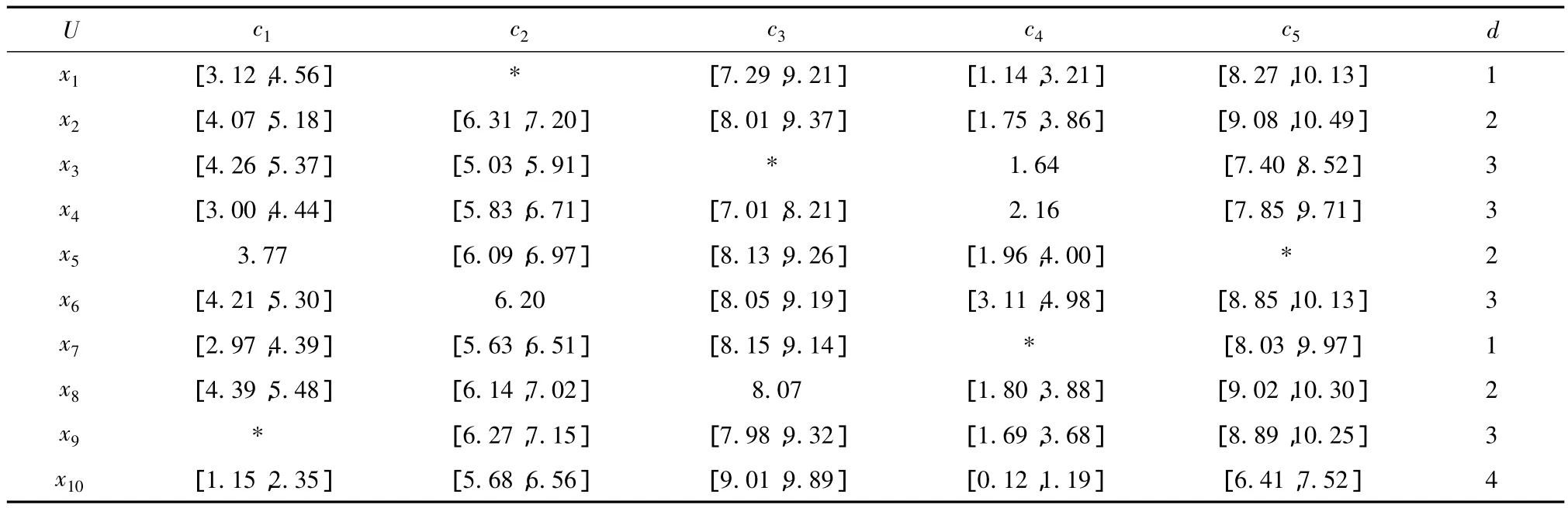
表1 不完备区间值决策信息系统

下面应用算法3.1来对该信息系统进行属性约简.具体步骤如下.

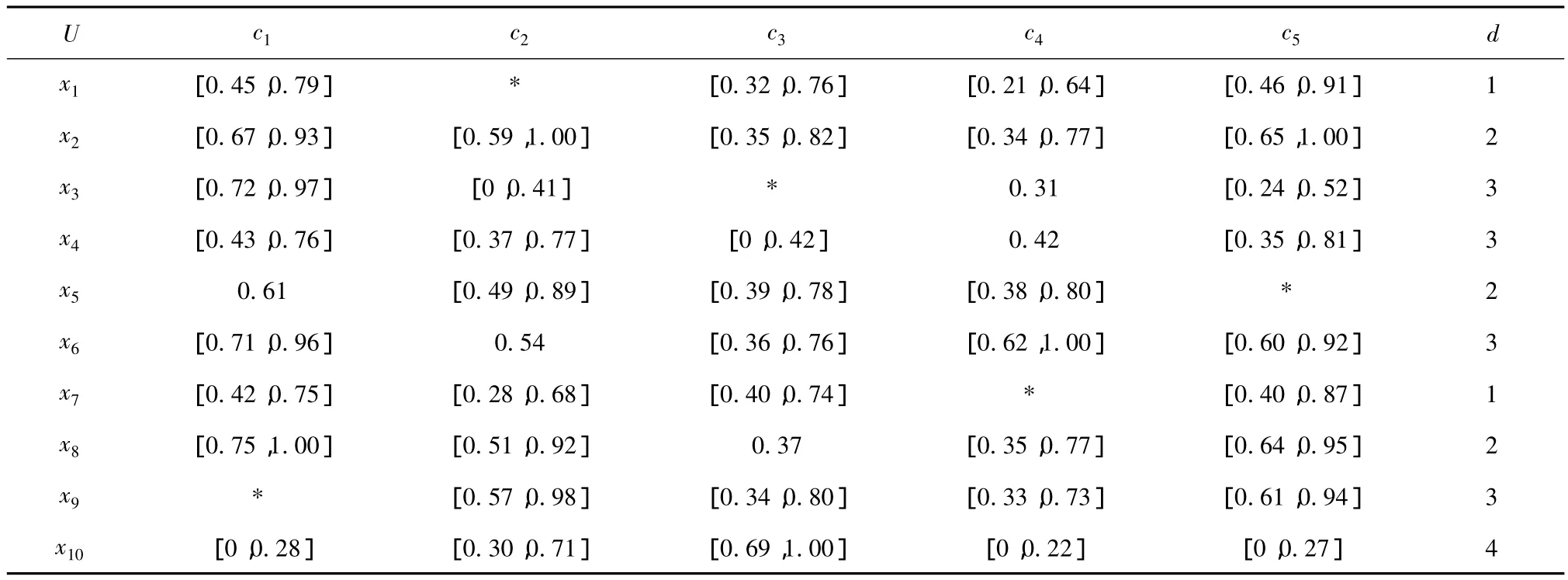
表2 规范化的决策信息系统

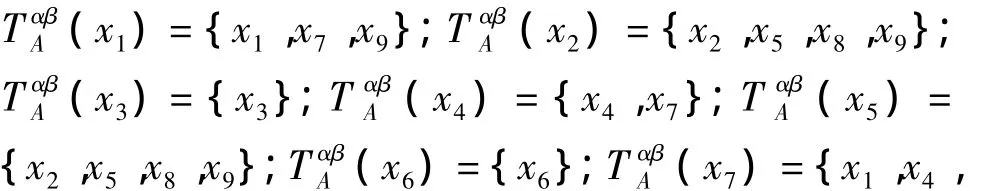
2)可求得u=0.53，t=0.76，再利用相似度公式求对象间的相似度.

3)求双精度相容类(xi)以及双精度极大相容类M.

取相似度阈值α=0.7，相似率阈值β=0.8有:

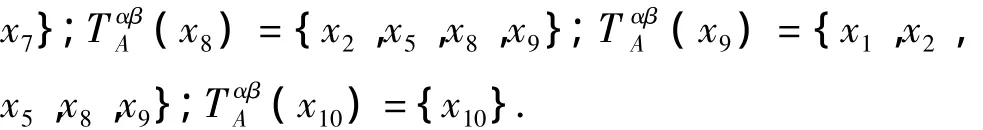
进而可求得双精度极大相容类为M1={x1，

4)根据决策属性d将论域进行划分，并求出对应的双精度极大相容类的上下近似.

因此可求得双精度极大相容类的上下近似为

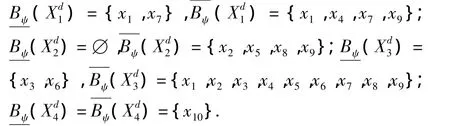
5)以双精度极大相容类构造区分矩阵见表3.

表3 不完备区间值信息系统K的区分矩阵

表3中有:

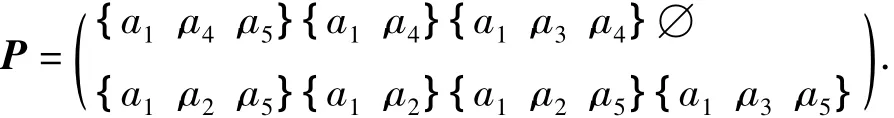
6)求得极大相容类集的约简和核为

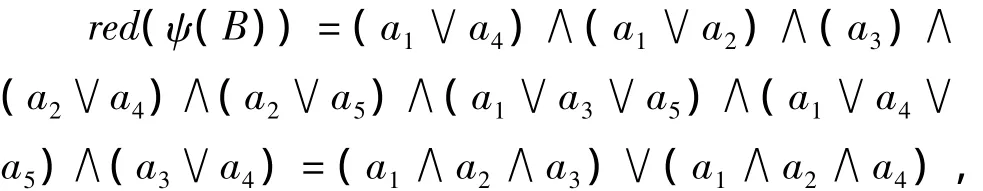
即极大相容类集的属性约简集为{a1，a2，a3}和{a1，a2，a4}，核为{a1，a2}.

5 结论

文中针对不完备区间值信息系统，建立了粗糙集拓展模型，采用极大相容类集逼近目标集的思想，推广了这个粗糙集拓展模型，并给出了不完备区间值信息系统的属性约简算法.结论如下:

1)相似度的改进，使得模型可以处理属性值大多数相交但不具备包含关系以及含多个连续值的情形，分类更加实际.

2)基于相似度和相似率的双精度容差关系，极大地利用了在双参数容差关系下不完备信息系统所能提供的信息，提高了逼近的精度.

3)所提出的粗糙集拓展模型可以处理更广泛的区间值信息系统数据类型，是一般的不完备区间值信息系统的粗糙集理论和方法.

References)

［1］Kryszkiewicz M.Rough set approach to incomplete information systems［J］.Information Sciences，1988，112(1/2/3/4):39-49.

［2］Stefanowski J，Tsoukiàs A.Incomplete information table and rough classification［J］.Computational Intelligence，2001，17(3):545-566.

［3］王国胤.Rough集理论在不完备信息系统中的扩充［J］.计算机研究和发展，2002，39(10):1238-1243.Wang Guoyin.Extension of rough set under incomplete information systems［J］.Journal of Computer Researchand Development，2002，39(10):1238-1243.(in Chinese)

［4］Graymala-busse J W.Discretization based on entropy and multiple scanning［J］.Entropy，2013，15:1486-1502.

［5］汪 凌.一种基于改进粒子群的连续属性离散化算法［J］.计算机工程与应用，2013，49(21):29-32.Wang Ling.Algorithem of continuous attribute discretization based on improved particle swarm［J］.Computer Engineering and Applications，2013，49(21):29-32.(in Chinese)

［6］刘小龙，江 虹，吴 丹.基于CACC的连续数据离散化改进算法［J］.计算机工程，2013，39(4):48-51.Liu Xiaolong，Jiang Hong，Wu Dan.Improved algorithm based on CACC for discretization of continuous data［J］.Computer Engineering，2013，39(4):48-51.(in Chinese)

［7］Yang Xibei，Yu Dongjun，Yang Jingyu，et al.Dominance-based rough set approach to incomplete intervalvalued information system［J］.Data＆Knowledge Engineering，2009，68(11):1331-1347.

［8］赵 亮，张 欣，薛 质.不完备区间值信息系统的安全评估［J］.计算机工程，2011，37(11):146-148.Zhao Liang，Zhang Xin，Xue Zhi.Security assessment for incomplete interval-valued information system［J］.Computer Engineering，2011，37(11):146-148.(in Chinese)

［9］魏利华，唐振民，丁 辉，等.不完备区间值信息系统中的粗集理论［J］.信息与控制，2009，38(3):286-292.Wei Lihua，Tang Zhenmin，Ding Hui，et al.Rough set theory in incomplete interval-valued information system［J］.Information and Control，2009，38(3):286-292.(in Chinese)

［10］陈子春，秦克云.区间值信息系统在变精度相容关系下的属性约简［J］.计算机科学，2009，36(3):163-166.Chen Zichun，Qin Keyun.Attribute reduction of interval-valued information system based on variable precision tolerance relation［J］.Computer Science，2009，36(3):163-166.(in Chinese)

［11］程利涛，李德玉，郑建兴，等.基于双参数相容关系的区间值信息系统属性约简［J］.山西大学学报:自然科学版，2011，34(3):363-367.Cheng Litao，Li Deyu，Zheng Jianxing，et al.Attribute reduction for interval-valued information systems based on dual-parameter tolerance relation［J］.Journal of Shanxi University:Natural Science Edition，2011，34(3):363-367.(in Chinese)

［12］Leung Yee，Li Deyu.Maximal consistent block technique for rule acquisition in incomplete information systems［J］.Information Sciences，2003，153:85-106.