机能分离型软钢阻尼器的性能
2014-12-23张超锋张志胜武美萍
张超锋,张志胜,武美萍,曹 毅
(1.江南大学机械工程学院,江苏无锡214122;2.东南大学机械工程学院,江苏南京211189)
近年来,低屈服点钢越来越广泛地应用于地震抗 震 工 程 中[1-3].其 中,由 于 极 低 屈 服 点 钢(LYS100,屈服强度100 N·mm2)具有变形能力大、低屈服强度以及较好的低周疲劳特性等优点,极低屈服点钢材尤其适合抗震阻尼器的设计和应用.
利用剪切面板设计软钢阻尼器是一种广泛采用的方法.然而,由于受肋板材料性能的影响,传统剪切型阻尼器的剪切变形能力(水平位移/高度)一般都不超过 20%[4-10].
为了提高剪切面板的变形能力,本研究中软钢材料被设计成肋板来改善面板角部的应力集中.水平力引起的弯矩则通过连杆来抵抗.连杆的强度足够大,并且连杆的长度和剪切板的高度相同时,剪切面板近似于受纯剪切变形.而连杆的长度相对于剪切板高度较长时,剪切面板做近似高度保持不变的简单剪切运动.因此,本研究通过试验改变连杆强度和连杆长度,同时借助图像处理技术分析阻尼器面板的应变变化,利用试验结果进行分析可有助于阻尼器的设计,提高阻尼器的吸能性能.
1 极软钢阻尼器
1.1 极软钢材料性能
拉伸试验得出的极软钢的屈服应力和极限应力分别是100 N·mm-2和275 N·mm-2,延伸率为60%,该材料极限强度是普通钢SS400的1/2,延伸率约为普通钢的3倍.
1.2 极软钢阻尼器的构造
图1为极软钢阻尼器结构.由图1可见:极软钢阻尼器的下端底板通过螺栓进行固定,而阻尼器的上端可以在水平方向进行自由移动.为了抵抗水平力引起的弯矩,在面板两侧设有连杆.为了防止面外变形,在面板上下方的横梁的前后两侧通过螺栓连接各设1个连杆.

图1 极软钢阻尼器结构
该极软钢面板宽w,高h和厚d分别为180,144和12 mm.宽厚比为

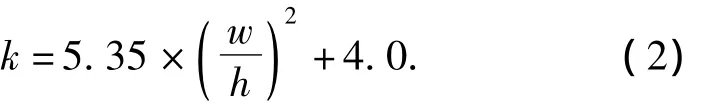
由此得该剪切板宽厚比约为0.065,此时面板不易出现面外屈曲,但面板4个角部的应力集中较大.
1.3 连 杆
1.3.1 连杆强度
图2为弯矩抵抗示意图.由图2可知:当水平力作用在阻尼器上端,所产生的弯矩由软钢面板和连杆共同抵抗.其中,当连杆间距离LD越大时,连杆所需抵抗力越小,反之则越大.为了使弯矩尽可能由连杆抵消,防止阻尼器面板发生塑性变形与连杆产生干涉,连杆间距离应采用较大值,但这也会加大阻尼器的尺寸,同时影响阻尼器的经济性.因此,310 mm和446 mm被采用.同时,为了让水平力作用到阻尼器的瞬间连杆就能够起到抵抗弯矩的作用,应尽量减小螺栓连接的孔与螺栓之间的间隙,间隙取值0.3 mm.系数k=1.3是通过下式计算得出:

图2 弯矩抵抗示意图
1.3.2 连杆长度系数
连杆和加载梁形成一个平行四边形结构,连杆绕着下端螺栓的圆心进行圆周运动,当水平力作用在上端的加载梁时,剪切面板会受到一定压缩力,该压缩力与连杆长度有关,如图3所示.
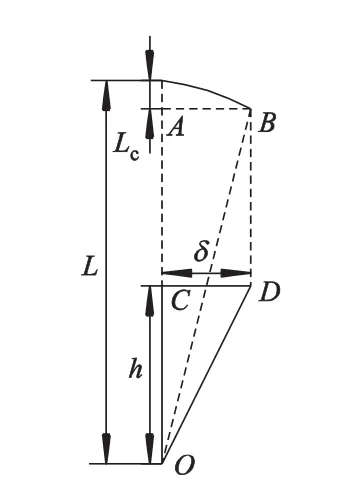
图3 面板运动轨迹
理想状态下,面板压缩变形与水平位移、连杆长有关,即

而水平位移与面板高度之比为剪切应变,即

由以上2个公式可得理想状态下面板的压缩应变为
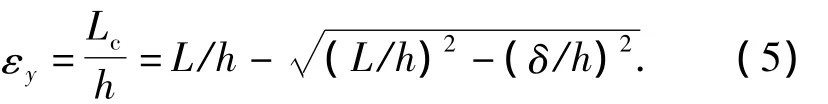
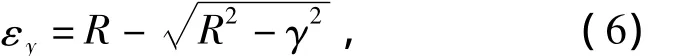
式中:L为连杆有效长度;δ为水平位移;γ为剪切应变;Lc为理想压缩变形.
上式表明当设计所要求达到的最大剪切应变为一定时,面板的压缩变形仅与连杆长度系数有关.当连杆长度系数较大时,剪切面板的压缩变形较小.但由于受安装空间高度的限制,连杆长度系数不宜取太大的值,本研究取值1.0和2.5进行比较.综上,极软钢阻尼器的试验试件名称及连杆长度系数如表1所示.

表1 试件名称及连杆长度系数列表
2 试验
2.1 设 备
试验通过将200 t静态千斤顶的一端固定在反力墙上,一端连接水平移动的加载梁.阻尼器通过12个高强度螺栓固定在底座上.为了消除试验加载设备引起的误差,在阻尼器上下两端设置2个激光位移器,这2个激光位移值的差作为阻尼器的水平位移,且作为加载控制量.阻尼器加载力通过千斤顶的内部测量计测得.
2.2 加载序列
探索阻尼器的变形能力是本研究的主要目标,兼顾到实际地震响应是一个往复加载的过程,因此本试验加载序列为往复渐增试验,渐增量为5%剪切应变.
2.3 图像处理
由于传统的应变计的量程无法满足大塑性应变要求,因此,本研究借助图像处理的方法测量剪切面板的应变.图像处理法是一种高精度的间接测量法,它通过CCD相机来测量面板上各个红点的位移.通过比较加载前、后面板上红点的变形量可求出整个面板的应变.
3 结果和讨论
3.1 破坏模式
阻尼器破坏模式如图4所示.由于该剪切面板宽厚比系数较小,因此极软钢阻尼器的破坏过程主要是塑性变形,产生裂纹直至断裂,而不是面外屈曲.FS1在30%剪切应变时肋板出现了紧缩变形,在40%剪切应变时肋板断裂(图4a).
阻尼器的力急剧下降.FS2.5破坏过程相对于FS1延迟了近5%剪切应变(图4b).
它们的破坏模式都可明显观察到一侧肋板的严重受拉变形.不同于FS系列的阻尼器的破坏模式,FL系列的破坏模式都是由面板角部的焊缝开裂所引起.35%剪切应变时,FL1角部出现了一些细微裂缝,随加载增大,阻尼器在45%剪切应变时,面板和肋板完全裂开(图4c),阻尼力急剧下降;与FL1破坏过程类似,FL2.5在55%时阻尼器断裂(图4d).

图4 阻尼器破坏模式
3.2 滞回曲线
阻尼器滞回曲线如图5所示.由图5可知:所有的阻尼力-剪切应变滞回曲线都呈纺锤形,可以被近似成完全弹塑性模型.试验试件 FS1,FS2.5,FL1和FL2.5的最大剪切应变分别为40%,45%,50%和55%,其对应的最大位移分别为50,55,60和65 mm.

图5 滞回曲线
3.3 连杆强度
当连杆间距离为310 mm时,FS系列阻尼器的肋板出现的拉伸变形表明:阻尼器上端加载梁和下端底座没有进行平行运动,连杆及其连接处没有足够强度抵抗弯矩,由此产生变形.经验证,连杆孔变形3 mm,这也导致了FS系列滞回曲线的弹塑性结合部出现了不规则形状.在增加了连杆间距离后(446 mm),连杆所要求的抵抗力下降,FL系列阻尼器避免了该种破坏模式,得到了理想的光滑滞回曲线.阻尼器FL1和FL2.5相对于FS1和FS2.5的变形能力都提高约10%剪切应变.因此,足够的抵抗弯矩的连杆强度对于保护阻尼器的性能具有重要作用.连杆强度不仅可以通过增加连杆截面实现,也可以通过适当增加连杆间距离来实现.
3.4 连杆长度系数
无论连杆的强度是否能够抵抗由水平力引起的弯矩,连杆系数大的 FS2.5和 FL2.5都比对应的FS1和FL1最大变形能力大5%剪切应变.这是由于连杆系数较大时,剪切板受到的压缩变形较小,反之压缩变形大.从图5c和d可明显观察到两者压缩变形量的差别,定量的分析可以通过图像处理来实现.由于FS系列的破坏模式受到连杆强度不足的影响,因此将FL系列阻尼器的面板图像处理结果用来分析及比较阻尼器的应变变化过程.FL1和FL2.5在20%和45%剪切应变时的阻尼器的米泽斯应变分布如图6所示.

图6 面板应变分布图
当加载的剪切应变为20%时,比较图6a和c,两者的最大应变都近似为0.2,但可以明显看出FL1两侧的应力集中比FL2.5大.
随着加载增加,应力集中的差值也越来越大,当加载的剪切应变为45%时,FL2.5(图6d)最大应变比FL1(图6b)要小0.15左右.阻尼器应变集中一般可通过应变集中系数评价,即

式中:Kt为应变集中系数;εmax为最大应变;εnom为平均应变.每个加载步结束时的FL系列阻尼器面板的米泽斯应变如表2所示.由表2可知:FL1和FL2.5的应变集中系数除了由于第一次加载时受材料不稳定影响而显示较大值外,其余两者应变集中系数都相对稳定,且平均值分别为2.15和1.64.由于前者应变集中系数较大,其变形能力相对于后者小了5%剪切应变.但由于载荷是渐增加载,前者累积塑性应变较后者有较大差距.

表2 应变变化过程
4 结论
1)连杆强度受连杆间距离影响.当连杆间距离较小时,所需连杆强度较大,反之则小.连杆长度系数较大时,阻尼器面板所受压缩变形较小,阻尼器变形能力高.连杆长度系数减小时,阻尼器变形能力会减小.
2)肋板采用极软钢材料时,相对于其他材料制成肋板的极软钢阻尼器的变形能力有极大提高.
3)极软钢阻尼器最大变形能力达到55%,该变形能力与拉伸试验最大变形量接近.这表明采用连杆方式可将软钢阻尼器极限性能发挥出来.
4)图像处理的结果能很好的预测以及分析阻尼器的破坏模式、滞回曲线.因此,在传统应变片无法满足测量要求时,图像处理是一个有效的方法.
5)借助图像处理不仅定性地得到极软钢阻尼器的破坏过程,而且可以定量分析阻尼器的应变变化,进行疲劳分析.
致谢
本试验在日本爱知工业大学耐震中心进行,感谢该中心员工对本项目的支持!
References)
[1]Susantha K A S,Aoki T,Kumano T,et al.Applicability of low-yield-strength steel for ductility improvement of steel bridge piers[J].Engineering Structures,2005,27:1064-1073.
[2]Masahiro T,Toshiaki F,Eiichi I.Study on hysteretic behavior of shear panel damper using low-yield-strength steel[C]∥Proceedings of Annual Meeting of the Architectural Institute of Japan.2005,9:967-977.
[3]Ge H B,Kaneko K,Usami T.A study on cyclic behavior and hysteretic model of high-performance stiffened shear panel dampers[C]∥Structural Engineering of JSCE.2010,56A:522-532.
[4]Koike Y,Yanaka T,Usami T,et al.An experimental study on developing high-performance stiffened shear panel dampers[C]∥Structural Engineering of JSCE.2008,54A:372-381.
[5]Ogawa S,Tokugawa K,Kato H,et al.Applicability of a steel damper against earthquake on middle-deck steel arch bridge[C]∥JSCE.2003:1-6.
[6]Tanaka K,Sasaki Y,Yoneyama S.An experimental study on hysteretic performance of shear panel dampers using different strength type of steel under static loading[J].Journal of AIJ,1999,520:117-124.
[7]Masahiro T,Toshiaki F,Eiichi I.Study on hysteretic behavior of shear panel damper using low-yield-strength steel[C]∥Proceedings of Annual Meeting of the Architectural Institute of Japan.2005:967-977.
[8]Ryosuke S,Kosuke M,Ryoichi T,et al.Experimental study on hysteretic behavior of shear panel damper using low-yield-strength steel[C]∥Proceedings of Annual Meeting of the Architectural Institute of Japan.2006:93-96.
[9]Takshiro S,Tomohiko M,Kouji I,et al.Static loading test and hysteretic model of shear panel using low-yieldstrength steel[C]∥Proceedings of Annual Meeting of the Architectural Institute of Japan.2001:181-184.
[10]Liu Y,Aoki T,Takaku T,et al.Cyclic loading tests of shear panel damper made of low-yield steel[C]∥Structural Engineering of JSCE.2007,53A:560-567.
