基于占空比干扰观测法的MPPT控制

蔡纪鹤，孙玉坤，3，黄永红

(1.江苏大学电气信息工程学院，江苏 镇江212013;2.江苏大学 机械工业设施农业测控技术与装备重点实验室，江苏 镇江212013;3.南京工程学院，江苏南京211167)

太阳能取之不尽、用之不竭、分布广泛、清洁无污染，是解决世界能源危机行之有效的绿色能源，而光伏并网发电是利用太阳能最有效的方式，起源于20世纪80年代初期［1-2］，最初大部分是由政府投资建设的大型光伏并网试验性电站.从20世纪90年代开始，鉴于光伏发电成本比较高，世界各发达国家为应对能源危机，实现经济和社会的可持续发展之路［3］，纷纷制定各种激励政策，刺激光伏产业的发展［4］，特别是近十多年来，光伏并网发电系统发展迅速［5］.虽然由于欧洲债务危机以及美国和欧盟和“双反”的影响，目前的光伏市场一片黯淡;但是，从长远来看，光伏产业的未来仍然值得憧憬.作为光伏并网发电关键技术之一的最大功率点跟踪(maximum power point tracking，MPPT)技术，关系到光伏阵列的光电转换效率，其性能对整个系统有至关重要的影响.

文中拟以光伏阵列等效电路作为切入点，分析光伏阵列获得最大功率的条件以及外界环境变化时最大功率点的跟踪过程;通过对BOOST电路中开关管的控制实现MPPT控制;提出基于占空比干扰观测法MPPT控制原理，并在Matlab环境下进行仿真研究.

1 MPPT原理

在一定的光照强度、工作温度及负载状态等条件下，光伏阵列具有特定的输出特性，其等效电路如图1所示.光伏阵列等效为电压源Upv和内阻Rpv串联的电路，Varray为光伏阵列的输出电压，Rl为负载电阻.

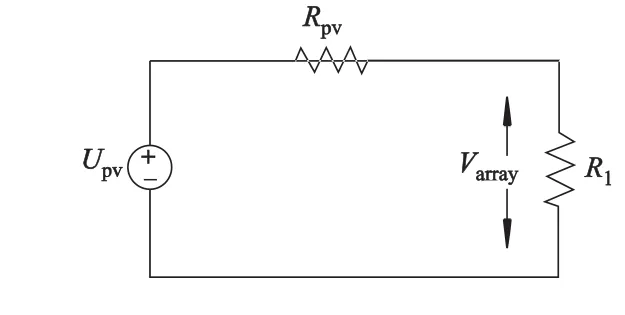
图1 光伏阵列等效电路

由戴维南定理可知，光伏阵列发出的功率Parray为

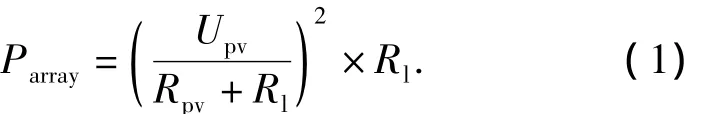
根据最大功率定理，当Rpv等于Rl时，Parray得到最大值，此时光伏阵列向负载Rl输出的功率最大.

根据式(1)光伏阵列输出功率的定义，在一定的工作条件下，可以在光伏阵列的I-V特性曲线上画出一系列等功率曲线，如图2所示，其中必有一条等功率曲线L1与光伏阵列I-V特性曲线相切，其切点就是最大功率点M.对于某一负载，其输出特性也是一定的，并有一条负载曲线与之相对应.根据式(1)，当负载Rl1的阻值与光伏阵列的内阻相等时，负载Rl1的负载曲线经过M点，此时称之为光伏阵列与负载完全匹配［6］.

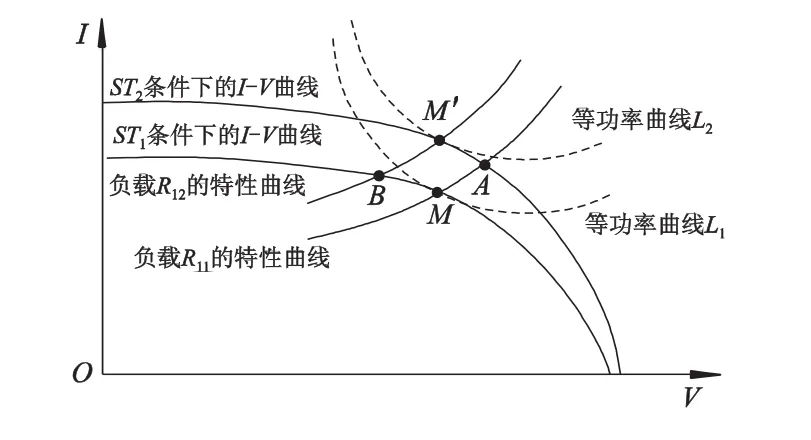
图2 MPPT控制过程

综上所述，要提高光伏并网发电系统的整体效率，一个有效的途径就是实时检测光伏阵列的输出功率，由一定的控制算法预测当前环境条件下光伏阵列可能的最大功率点，并通过改变系统负载特性的方法来实现调整光伏阵列工作点，从而实现在不同的太阳光辐射度和光伏阵列工作温度下始终让光伏阵列工作在最大功率点附近.

2 MPPT控制实现方式

光伏并网发电系统根据实现MPPT控制位置的不同，可分为单级式系统和两级式系统.其中单级式系统只具有一个能量变换环节，MPPT、逆变、并网均由并网逆变器来完成，算法复杂，对系统的耐压等级要求高［7］.而两级式系统由BOOST变换器和并网逆变器构成，BOOST变换器完成升压和MPPT功能，并网逆变器完成逆变、并网功能［8］.两级式系统中的BOOST变换器和并网逆变器具有相对独立的控制结构，前后级耦合小，且控制实现相对简单，对环境变化适应范围较广，因此，得到了广泛的应用.

文中采用两级式结构，并通过对BOOST变换器中开关管的不断导通和关断控制，达到改变光伏阵列输出电压Varray的目的，从而改变系统的负载特性，实现MPPT控制.

图3为BOOST变换器的拓扑结构，图中，Varray为光伏阵列的输出电压，也即前级BOOST变换器的输入电压;Udc为前级BOOST变换器的输出电压，也即后级并网逆变器的输入直流侧电压.在Udc恒定的情况下，通过对BOOST电路中开关管Sb的控制，也即MPPT控制，就可以实现对Varray的控制，使光伏阵列工作在最大功率点处.

图3 BOOST变换器

BOOST变换器的工作原理如图4所示.

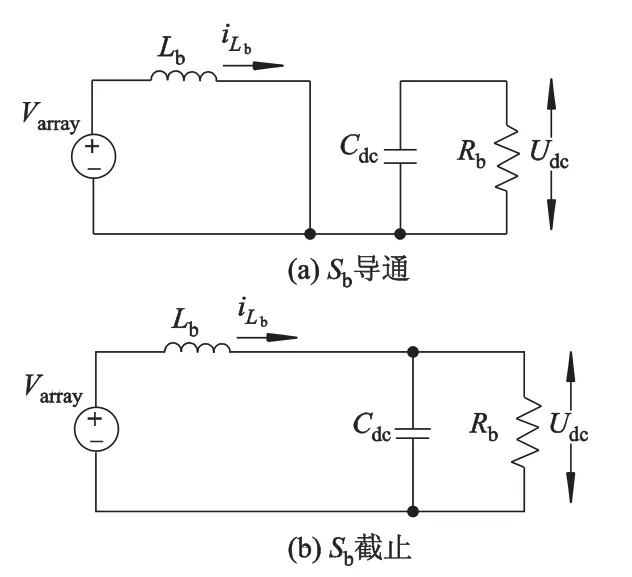
图4 BOOST变换器两种工作状态时等效电路图

定义开关管Sb导通时间ton与开关周期TS的比值为占空比，用D表示:

当BOOST电路的滤波电感Lb和滤波电容Cdc足够大时，BOOST电路的电感电流iLb工作在连续模式，且由于滤波电感Lb的时间常数远远大于开关周期，因此滤波电感电流iLb的变化可近似认为是线性的.

目前，预防鸡啄癖最主要的方法是适时断啄，尤其是饲养期间密度较高的鸡群。在给予处理期间，可以使用电动去啄器、铬铁等器械，将雏鸡的啄尖去掉，必要时后期要再次去除。断啄需要在鸡7～10日龄或4～5周龄时进行。在断啄期间也可以进行转群、换笼等，但要避免14周龄以上的鸡进行断啄，以免流血过多[1]。

在开关管Sb导通期间(0～t1)，电感电流iLb的增量为

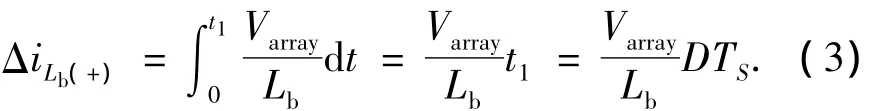
在开关管Sb截止期间(t1～t2)，电感电流iLb的减小的绝对值为

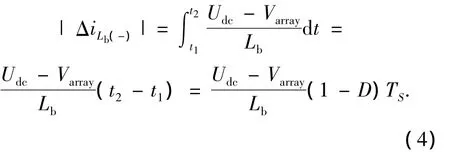
当电路工作在稳态时，电感电流iLb的波形必然周期重复，开关管Sb导通期间电感中电流的增加量等于其截至时电感中电流的减少量，即

联合式(3)-(5)可得

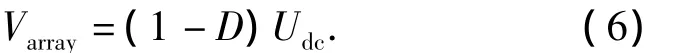
上式表明，通过改变光伏阵列输出电压Varray的方法既可以调整系统直流侧电压Udc，也可以改变BOOST电路中开关管的占空比D.对于光伏并网发电系统来说，为了保证整个系统的可靠运行，其直流侧电压Udc的电压值必须稳定.因此，通常采用控制占空比的方式来改变光伏阵列输出电压Varray，从而达到最大功率点跟踪控制的目的.占空比D与光伏阵列输出电压Varray成反比，占空比的改变通常采用PWM调制法，如图5所示.其中，D为占空比调制信号，St为三角波载波信号，将占空比调制信号与三角载波信号比较后得到的Δr作为PWM控制信号，驱动BOOST电路的开关管Sb，从而实现光伏阵列的最大功率点跟踪控制.

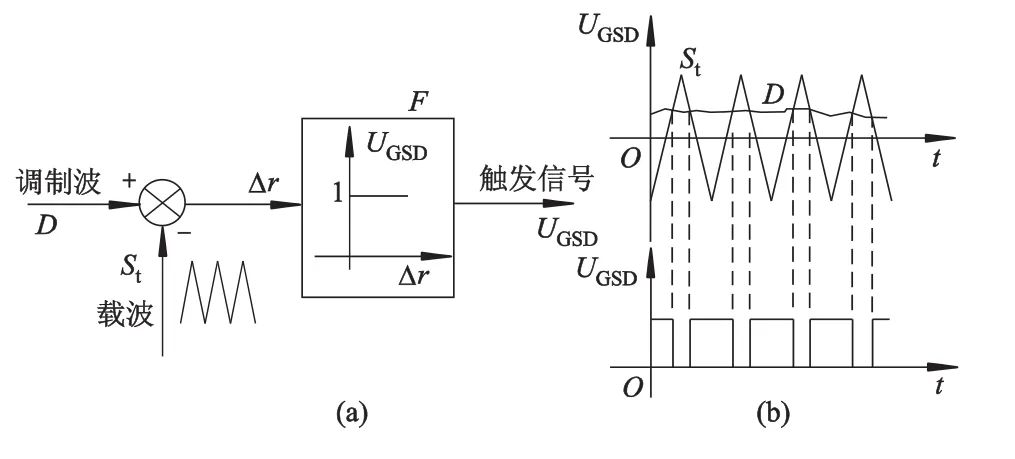
图5 占空比的PWM调制法

3 占空比干扰观测法控制原理

干扰观测法是目前MPPT控制方法中应用最为广泛、研究最多的一种方法［9-10］.其工作原理如下:对每个采样周期内光伏阵列的输出电压ΔU和输出电流进行不断采样，并将其相乘，可得到该采样周期内的输出功率ΔP;检测并计算该采样周期内的输出电压、输出功率与前一个采样周期的输出电压、输出功率的变化情况，从而确定输出电压的调整方向，再根据输出电压与占空比的关系调整占空比，设输出电压增大的方向为正向调整方向，输出电压减小的方向为反向调整方向，电压调整过程如表1所示.

表1 干扰观测法电压调整过程

由表1可知，当ΔU×ΔP的符号为正时，系统应在下一控制周期正向调整输出电压，使得输出电压增大，工作点向最大功率点方向移动;当ΔU×ΔP的符号为负时，系统应在下一控制周期反向调整输出电压，使得输出电压减小，工作点向最大功率点方向移动;如此反复循环，直至输出电压稳定于设定的一个很小偏差范围内，即可认为系统达到最大功率点.占空比干扰观测法的控制流程如图6所示.

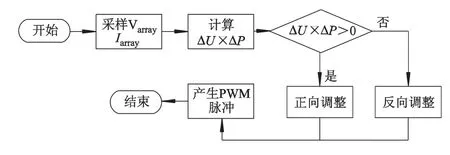
图6 占空比干扰观测法控制流程图

4 仿真结果

在Matlab仿真平台下按照图6所示流程搭建占空比扰动观测法控制模型.其仿真参数如下:太阳光辐射度为1 000 W·m-2，光伏阵列工作温度为25℃;光伏组件参数为Pmax=185 W，Vm=37.5 V，Im=4.92 A，Voc=44.5 V，Isc=5.4 A;光伏组件采用6 串9并的方式构成10 kW的光伏阵列;采用双极性PWM调制方式，三角载波的频率为2 000 Hz.

采用改变太阳光辐射度的方法来检测系统在不同环境下的适应能力以及动态响应能力，仿真结果如图7所示.

图7 不同太阳光辐射度下光伏阵列的电压、功率曲线

从图7所示的动态响应曲线可以看出，在0.10 s及0.20 s时刻，太阳光辐射度发生剧烈变化，由1 000 W·m-2变为600 W·m-2再变回1 000 W·m-2，此时，系统能够迅速调整工作点，使光伏阵列的输出电压由224 V变为205 V再变为224 V左右，与光伏阵列的最大工作点非常接近(太阳光辐射度为1 000 W·m-2为225 V，太阳光辐射度为600 W·m-2为208 V).图8，9给出了恒电压控制法和占空比干扰观测法功率曲线.

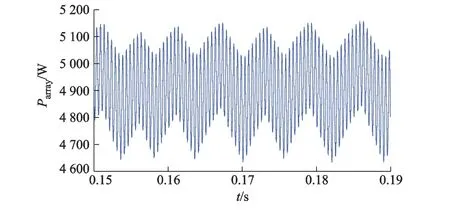
图8 恒电压控制法功率曲线(S=600 W·m-2)

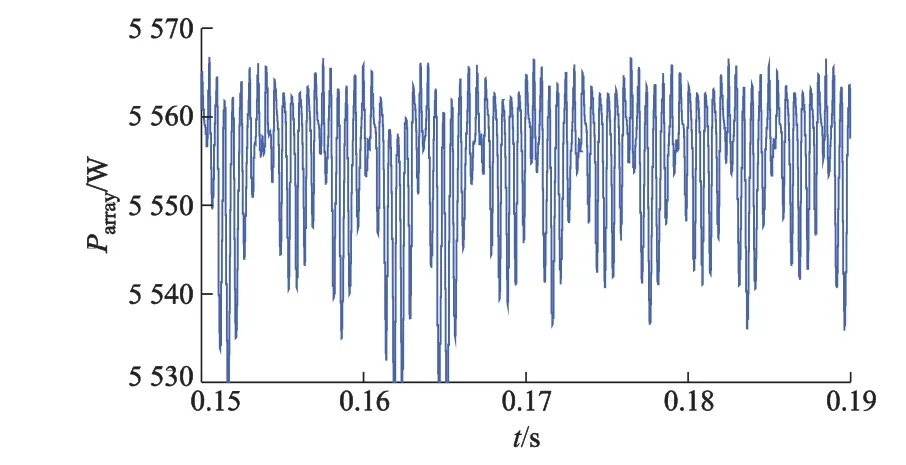
图9 占空比干扰观测法功率曲线(S=600 W·m-2)

从图8，9可以进一步看出，在太阳光辐射度变为600 W·m-2时，采用占空比干扰观测法输出功率的平均值大约为5 555 W，而采用恒电压控制法［11］输出功率的平均值大约为4 900 W，损失了相当一部分功率.其差值大约为655 W，对于一个10 kW的系统来说，相当于系统最大功率输出的6.5%，对于MW，GW级的光伏电站来说，采用恒电压控制法的功率损失将更加可怕.因此，恒电压控制法也仅仅适用于小型光伏离网系统，占空比干扰观测法精度较高，得到了广泛应用.

5 结论

文中采用占空比干扰观测法进行MPPT控制，结论如下:

1)由于采用电压、电流的实时采样，能够根据系统运行情况进行实时MPPT控制，精度较高.

2)MPPT控制具有很好的跟踪效果，其动态响应快、稳态误差较小，在太阳光辐射度发生变化时，能够迅速调整工作点，使光伏阵列运行在最大功率点附近.

3)占空比干扰观测法由于直接把占空比作为控制变量，只需要控制一个参数，从而使控制器结构简单，控制方便，降低了设备投资，非常利于工程应用.

References)

［1］Bergauer-Culver B，Jager C.Estimation of the energy output of a photovoltaic power plant in the Austrian alps［J］.Solar Energy，1998，62(5):319-324.

［2］Oman H.Space solar power development［J］.IEEE AES Systems Magazine，2000，152:3-8.

［3］廖志凌，刘国海，梅从立.一种改进的硅太阳能电池非线性工程数学模型［J］.江苏大学学报:自然科学版，2010，31(4):442-446.Liao Zhiling，Liu Guohai，Mei Congli.An improved non-linear engineering mathematical model for silicon solar cell［J］.Journal of Jiangsu University:Natural Science Edition:2010，31(4):442-446.(in Chinese)

［4］查晓明，刘 飞.光伏发电系统并网控制技术现状与发展(上)［J］.变频器世界，2010(2):37-42.Cha Xiaoming，Liu Fei.The present situation and development of grid connected control for photovoltaic power system(1)［J］.The World of Inverters，2010(2):37-42.(in Chinese)

［5］Quamruzzaman Muhammad，Rahman Kazi Mujibur.Development of a new phase-angle controlled grid-connected PV system［C］∥Proceedings of the6th International Conference on Electrical and Computer Engineering.Dhaka，Bangladesh:IEEE Computer Society，2010:82-85.

［6］赵争鸣，陈 剑，孙晓瑛.太阳能光伏发电最大功率点跟踪技术［M］.北京:电子工业出版社，2012.

［7］Petreuş D，Dărăban Ş，Ciocan I，et al.Single-stage low cost grid connected inverter in photovoltaic energy applications［C］∥Proceedings of the15th International Power Electronics and Motion Control Conference.Novi Sad， Serbia:IEEE ComputerSociety，2012，doi:10.1109/EPEPEMC.2012.6397351.

［8］Zhou Xiaojie，Ruan Yi.Research on two-stage threephase photovoltaic grid-connected system［J］.Advanced Materials Research，2012，535/536/537:1247-1251.

［9］Palizban Omid，Mekhilef Saad.Modeling and control of photovoltaic panels base perturbation and observation MPPT method［C］∥Proceedings of the2011IEEE International Conference on Control System，Computing and Engineering.Penang，Malaysia:IEEE Computer Society，2011:393-398.

［10］刘邦银，段善旭，刘 飞，等.基于改进扰动观察法的光伏阵列最大功率点跟踪［J］.电工技术学报，2009，24(6):91-94.Liu Bangyin，Duan Shanxu，Liu Fei，et al.Photovoltaic array maximum power point tracking based on improved perturbation and observation method［J］.Transactions of China Electrotechnical Society，2009，24(6):91-94.(in Chinese)

［11］Li Jiyong，Gong Renxi，Feng Zhaohe.A novel MPPT intelligent multiple method based on constant voltage method and fuzzy control applied in photovoltaic power system［J］.Advanced Science Letters，2012，11(1):184-188.