基于循环和对称边界的图像反卷积快速算法
2014-12-23徐梦娜金文清韩玉兵
徐梦娜,蔡 信,金文清,韩玉兵
(南京理工大学 电子工程与光电技术学院,江苏 南京210094)
0 引 言
在现实生活中有很多因素会导致图像降质,如果把图像降质过程用一个卷积来描述,那么图像复原就可以用反卷积来实现。但这通常是个反问题,反问题所共有的一个问题是病态性,需要正则化来修改最终的解。常用的正则化参数选取方法主要有经验选取方法、广义交叉验证方法GCV (generalize cross validation)、L-Curve方法,但这些方法通常需要图像先验知识或是计算量很大。近年来一种动态自适应的参数选取方法应用越来越广泛,Eldar将这种方法推广到图像反卷积[1]中,R.Giryes在此基础上又结合了小波的概念[2]。但在这些反卷积算法中多需要写出具体的表达式,而大部分的算法是非线性的,无法写出具体的表达式。我们的方法通过给出迭代表达式而不是具体算式规避了这些缺点,并且由于模糊矩阵的高度结构化,通过边界条件的选择可以大大缩小时间效益[3-5]。
1 卷积快速算法
一般地,图像的降质模型可表示为
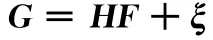
其中,F 为原图像,G 为观测到的降质图像,H 为降质模型的确定性部分,一般假设为一个线性算子,代表图像获取过程中的各种扭曲、模糊及降采样等,ξ 为加性噪声部分。反卷积就是从观测图像G 中尽可能复原出F,这显然是一个病态反问题,本文采用著名的total variation (TV)正则化以及Split Bregman方法[6]来求解,则有迭代算法
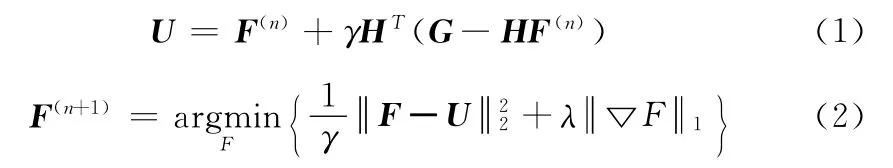
对于式 (2),采用文献 [7]中的TV 去噪方法来求解,正则化参数λ的选取采用文献 [8]中方法。TV 模型中,最重要的结构,模糊HF 及其转置操作HTG,在适当的边界条件下可以被看成离散卷积,如何使这个结构达到最好的效益就是我们所关心的[9]。一种有效的降低计算成本的方法就是设计快速算法来实现卷积操作,本文将主要讨论周期边界和对称边界条件下的两种计算的快速算法。
1.1 基于循环边界的DFT快速算法
循环边界条件是指超出图像边界的像素数据是未超出部分的完整复制,基于这种边界条件,模糊矩阵是一个块循环矩阵,这些矩阵能被离散傅里叶矩阵对角化,因此通过傅里叶变换就很容易找到其逆矩阵[10]。为简单起见,先从一维信号开始,假设一维原信号f’= (…,f-m+1,…,f0,f1,…,fn,fn+1,…,fn+m,…)T,模糊函 数为h= (…,0,0,h-m,h-m+1,…,h0,…,hm-1,hm,0,0,…)T,则卷积可表示为

由式 (3)可知,g 不仅仅由 (f1,…,fn)T决定,还由 (f-m+1,…,f0)T和 (fn+1,…,fn+m)T决定。在加上边界条件之前,我们先将式 (3)重新写为[11]

其中
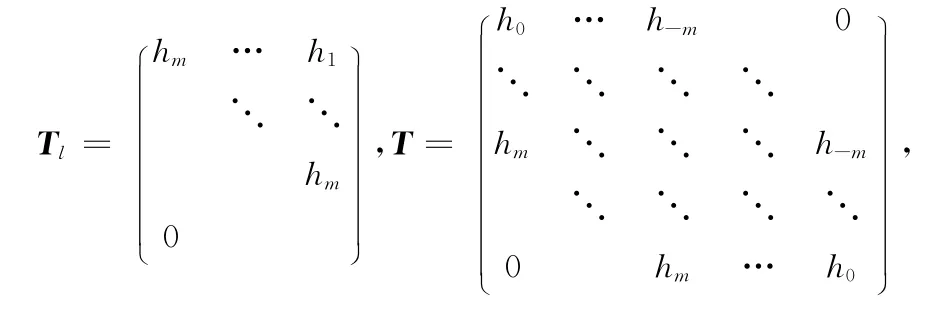
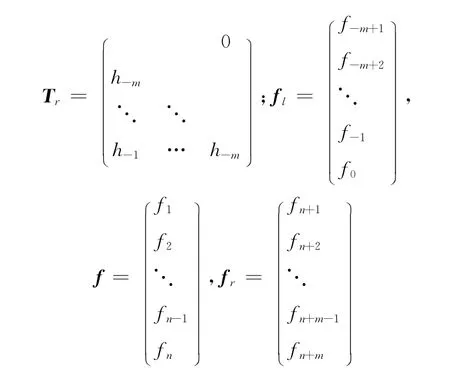
当设定循环边界条件,在式 (3)对所有j有fj=fnj,则式 (4)可写为

其中, (0|Tl)和 (Tr|0)是对Tl和Tr分别加上 (nm)列0后得到的n×n Toeplitz矩阵。加上循环边界条件后最大的优势就是H 是一个循环矩阵,可以被离散傅里叶矩阵对角化,从而大大地减低运算问题。令

由矩阵乘法可得Hwk=λkwk,k=0,1,…,m-1,再由矩阵理论可知,λk是循环矩阵H 的特征根,而wk是该矩阵H 对应于此特征根的特征向量,将m 个wk排成矩阵W= [w0w1w2… wm-1],就可以将H 表达成特征分解的形式H=WΛW-1,式中Λ=diag {λ0,λ1,…,λm-1}为对角矩阵。利用以上的式子,容易得出
上述结论可以推广到二维函数的分块循环矩阵中[10,12],与一维函数的循环矩阵对角化思路一样,可使二维函数的分块循环矩阵对角化。设H 是一个m1m2×m1m2块循环矩阵,先将卷积函数h补零使尺寸扩展到m1×m2,然后作离散傅里叶变换,记为B(μ,ν),易验证H 有特征分解式H=WΛW-1。其中W 是H 的特征向量排成的矩阵,是非奇异的,Λ 是对角矩阵,它是通过把B(μ,ν)的m1×m2个元素从第一行起,逐个顺序填入m1m2×m1m2对角阵构成。H 的特征矩阵W 和W-1之前的关系可以验证得到

由此可采用离散傅里叶变换来处理,不需要实际地存放和处理大尺度的矩阵H。
根据以上理论,我们给出一个简单的算例
采用MATLAB 内置函 数imfilter(X,h,’circular’)以及DFT 算法得到卷积X*h的结果如式 (6)所示

采用编写的Matlab程序ImfilterTranspose()函数以及DFT 算法得到HTX 的结果如式 (7)所示
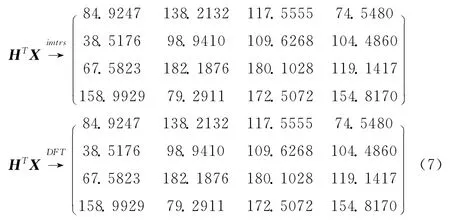
由式 (6)、式 (7)可知,由卷积方法得到的结果与DFT 方法得到的结果一致,证明基于循环边界的卷积可以由DFT 代替。
1.2 基于对称边界的DCT快速算法
对称边界条件是指超出图像边界的像素数据是未超出部分的镜像对称映射,基于这种边界条件,模糊矩阵不再是一个块循环矩阵,而是块Toeplitz加Hankel矩阵 (block Toeplitz-plus-Hankel matrix),尽 管 这 种 矩 阵 的 结 构 更 复杂,但也能被离散余弦矩阵对角化[4,11],因此通过离散余弦变换也很容易找到其逆矩阵。
为简单起见,也从一维反卷积开始,当设定对称边界条件,在式 (3)中有
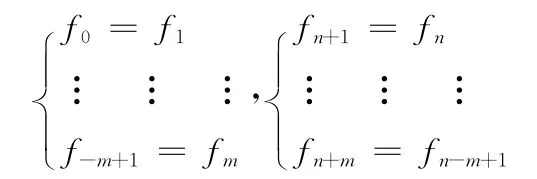
基于以上理论,则式 (4)可写为
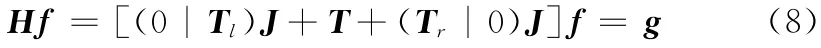
其中,J 是n×n逆矩阵。
首先定义C 为n×n离散余弦变换矩阵

其中,δi,j为克罗内克函数,C 是正交的,则有CTC=CCT=I,同时,对于任何n维向量v,Cv和CTv 都能通过DCT 的实部操作来得到。定义Γ= {CTΛC|Λ 为n×n对称阵}是空间包含所有能被C 对角化的矩阵,令Q=CTΛC∈Γ,对CQ=ΛC 两边同乘e1= (1,0,…,0)T,可得到Q 的特征值
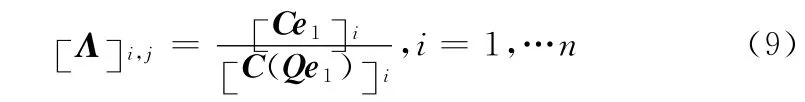
由式 (9),Q 的特征值能够通过对Q 的第一列做一次DCT 得到,事实上,在Γ 里的所有矩阵都是由其第一列决定的。再定义向量v= (v0,v1,…,vn-1)T的转移为σ(v)≡ (v1,v2,…,vn-1)T,T(v)是 以v 为 第 一 列 的n×n对称Toeplitz矩阵,H(x,y)是以x 为第一列向量,以y为最后一列向量的n×n Hankel矩阵[11]。下面再给出几个定理:
引理1[13]设Γ 是所有能被离散余弦变换C 对角化的矩阵集,则
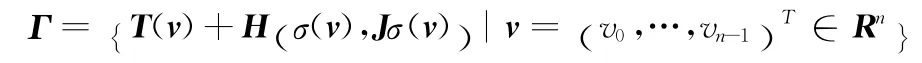
从引理1可以看出能被C 对角化的矩阵是一些特殊的Toeplitz加Hankel矩阵。
定理1[11]模糊函数h 是对称的,则对所有i有hi=h-i,则式 (8)中H 能被重新写为

其中,u= (h0,h1,…,0,…,0)T。
由定理1就能得到式 (8)中的解f 由f=CΛ-1CTg 得到,其中Λ 是由H 特征值组成的对角矩阵,可由一次DCT变换得到。因此f 能由3次DCT 变换得到。
一维的结果可以很容易地拓展到二维,在对称边界条件下,H 是块Toeplitz和Hankel矩阵。
定理2[11]假如模糊函数hi,j是对称的,则对所有i,j有hi,j=hi,-j=h-i,j=h-i,-j,则H 能被二维离散余弦变换矩阵CC 对角化,其中为张量积。
令P 为置换 矩 阵 满 足 [PTΛP]i,j;k,l= [Λ]k,l;i,j,1≤i,j≤n,1≤k,l≤n,其中Λ 中第 (k,l)个块中的第 (i,j)个数被第 (i,j)个块中的第 (k,l)个数置换,则有PT(C I)P=(IC)及PTΛP =,是由块矩阵构成的对角阵,每个都和式 (8)中的H 有相同的形式,则对所有j有C=,是一个对角阵,则有

根据以上理论,基于MATLAB7.9.0.529版本,我们也给出一个简单的算例:
采用MATLAB内置函数imfilter(X,h,'symmetric')以及DCT 算法得到卷积X*h的结果如式 (11)所示

采用编写的Matlab程序ImfilterTranspose()函数以及DCT 算法计算HTX 得到的结果如式 (12)所示

由式 (11)、式 (12)可知,卷积方法得到的结果与DCT 方法得到的结果一致,证明基于对称边界的卷积可以由DCT 代替。
2 实验研究
将以上算法应用在TV 正则化的图像反卷积中,模糊算子采用标准差0.8的5×5高斯模糊核,噪声方差为0.05(灰度值归一化为 [0,1]),对图像进行反卷积重建,实验平台基于Matlab7.9.0.525 版本,CPU 速度为2GHZ,内存为1GHZ 的32 位操作系统。选用大小为256×256 的Cameraman及Peppers图像,给定循环边界条件,在迭代算法中应用DFT 快速算法,结果分别如图1及图2所示。选用大小为256×256的Boats及Elaine图像,给定对称边界的条件,在迭代算法中应用DCT 快速算法,结果分别如图3及图4所示。

由图1-图4可以看出,反卷积都取得了比较好的效果,较大程度地恢复出了原图像。在此基础上,我们再来比较这两种快速算法的时间效益以及图像的信噪比提高情况,信噪比计算公式采用下式
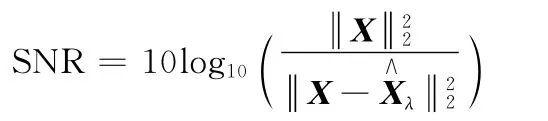
结果如表1,表2所示,其中计算时间是对应一个正则化参数的完整的反卷积过程。

表1 卷积方法与DFT 方法对比

表2 卷积方法与DCT 方法对比
由表1,表2可以看出,不论是基于循环边界条件还是对称边界条件,图像输出信噪比得到明显提高,基于这两种边界的快速算法在计算中也节省了大量的时间。
3 结束语
在图像反卷积算法中,采用正则化的方法来寻找解,但由于模糊矩阵十分庞大,在实际计算时不易显式得到和存储,尤其是在计算矩阵转置的时候,很难实现,但是在多数迭代算法中又需要用到。为了减少运算时间,根据图像卷积时特殊边界的特性,对基于循环边界条件和对称边界条件的图像,在需要计算模糊矩阵及其转置矩阵的时候,可以分别用DFT 及DCT 快速算法来实现,既能节约计算时间,又能准确地保证图像复原质量。实验结果已经表明该算法适用不同的图像并都能取得良好的效果。
[1]Eldar Y.Generalized SURE for exponential families:Applications to regularization [J].IEEE Trans Signal Process,2009,57 (2):471-481.
[2]Giryes R,Elad M,Eldar Y C.The projected GSURE for automatic parameter tuning in iterative shrinkage methods[J].Appl Comput Harmon Anal,2010,3 (30):407-422.
[3]Shi Y,Chang Q.Acceleration methods for image restoration problem with different boundary conditions [J].Appl Numer Math,2008,58 (5):606-614.
[4]Lv X G,Song Y Z,Wang S X.Image restoration with a highorder total variation minimization method [J].Applied Mathematical Modelling,2013,37 (16-17):8210-8224.
[5]Ji H,Wang K.Robust image deblurring with an inaccurate blur kernel[J].IEEE Trans Image Process,2012,21 (4):1624-1634.
[6]Goldstein T,Osher S.The split bregman method for L1-regularized problems[J].SLAM Journal on Imaging Science,2009,2 (2):323-343.
[7]Getreuer P.Rudin-osher_fatemi total variation denoising using split bregman [OL/J].Image Processing on Line,http://dx.doi.org/10.5201/ipol.2012.g-tvd,2012.
[8]Ramini S,Blu T,Unser M.Monte-carlo sure:A black-box optimization of regularization parameters for general denoising algorithms[J].IEEE Trans Image Process,2008,17 (9):1540-1554.
[9]Wang Yulun,Yang Junfeng,Yin Wotao,et al.A new alternating minimization algorithm for total variation image reconstruction [J].SIAM J Imag Sci,2008,1 (3):248-272.
[10]Gonzalez R,Woods R.Digital image processing [M].New York:Addison Wesley,1992.
[11]Michael K,Raymond H,Wun Cheung.A fast algorithms for deblurring models with neumann boundary conditions[J].SIAM J Sci ComPut,1999,21 (3):851-866.
[12]MIAO Qing.The research and application of regularization in image restoration [D].Changsha:National Defense Science and Technology University,2005:17-19 (in Chinese).[苗晴.图像复原中正则化方法的研究及应用 [D].长沙:国防科学技术大学,2005:17-19.]
[13]Chan R,Chan T,Wong C.Cosine transform based preconditioners for total variation deblurring [J].IEEE Trans Image Processing,1999,8 (10):1472-1478.
[14]Getreuer P.Total variation deconvolution using split bregman[J/OL].Image Processing on Line,http://dx.doi.org/10.5201/ipol.2012.g-tvd,2012.
