基于叶节点DFS序列的网络拓扑推断算法

石佳玉，吴辰文，孔德弟，张耀方

（兰州交通大学 电子与信息工程学院，甘肃 兰州730070）

0 引 言

本文的具体重点是减少拓扑推断过程中需要的成对探测包的总数，以便高效地解决网络拓扑重构的问题。本文针对单播断层扫描［1］探测方法，只需要外部端到端节点的基本测量，不需要中间节点的协作［2］。利用叶节点的深度优先搜索 （DFS）序列［3］，以下简称叶节点的DFS 序列，并且巧妙的利用了相关性矩阵的特殊结构，找出具有共同祖先节点的叶节点，有效的减少成对探测包的数量，提高了拓扑推断的效率。对于一个平衡 叉树，以往所研究的基于聚类算法［2］的单播网络断层扫描拓扑推断技术需要的成对探测包的数量级为O（N2），且需要满足的假定条件太过严格，本文提出的利用叶节点DFS序列来推断拓扑结构的算法，只使用数量级为O（Nlog（N））的成对探测包，且明显的减少了相关性条件的限制，降低了算法的复杂度。

1 深度优先搜索 （DFS）序列

使用深度优先搜索 （DFS）方法遍历一棵 叉树的规则是先从根节点开始，然后逐步向下搜索每一个节点，并且标记每个节点，然后回溯，直到所有的节点被充分遍历（即每个孩子节点已被标记）。这样，一棵树的每个叶节点被遍历的先后顺序就会有所不同，我们将通过深度优先搜索的方法遍历得到的叶节点的排序称为深度优先搜索（DFS）序列。

定义 一个DFS序列，πDFS：｛1.2，…N｝→ ｛1.2，…N｝，在一个逻辑树结构T 中，按照深度优先搜索方法找到的叶节点的排序，同时也揭示了其内部节点的深度优先搜索顺序。

如图1所示，我们可以发现下面的DFS序列，所有这些序列都对应特定的深度优先搜索树的拓扑结构：

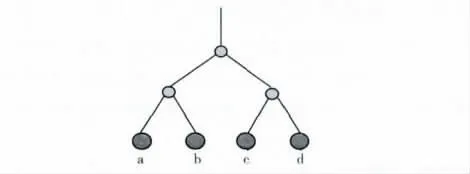
图1 简单的逻辑拓扑结构中的DFS序列

同时也有很多不满足深度优先搜索顺序的叶节点序列，如 ｛a，c，d，b｝.以上面DFS序列中的 ｛a，b，c，d｝为例，我们可以找到这组叶节点满足的共享路径矩阵PDFS

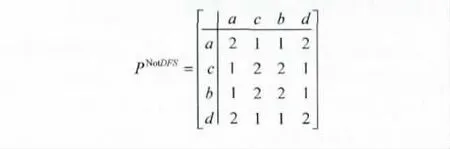
将共享路径的长度记为pi，j，即从根节点到这两个叶节点xi，xj之间共享路径中的共享节点的数量。如下面矩阵所示，PDFSa，b＝2表示从根节点到叶节点a，b有两个共享节点 （如图1所示）。以 ｛a，c，d，b｝为例，不满足DFS序列的共享路径矩阵PNotDFS如下所示

将网络中的两个终端记为xi，xj。利用断层扫描技术，可以测量到端节点之间的成对相关性［4］，记为si，j（例如，两个端节点之间的时延协方差和丢包率等）我们将重点放在这些成对的相关性是如何在特定的条件下生成与之符合的底层网络树的拓扑结构。

命题1：给定一组叶节点DFS序列，则共享路径矩阵P 满足如下条，pi，i＋1≥pi，i＋k，k＝｛1，2，…，N－i｝，i＝｛1，2，…，N－1｝。

证明：假设pi，i＋j≤pi，i＋k（0≤j≤k），则说明叶节点xi与xi＋j比叶节点xi和xi＋k具有更多的共享节点，即具有更长的共享路径。然而，在使用深度优先搜索方法遍历拓扑树的过程中，要求j＞k，也就是说节点xi＋k较节点xi＋j先被遍历，这与我们的假设相违背。因此，如果叶节点的序列满足DFS排序，则命题1的结论成立。

2 算法描述

本算法分为两个主要部分：使用递归二分法找出叶节点的DFS序列；使用DFS序列推断逻辑拓扑树的结构。

2.1 递归二分法找出叶节点的DFS序列

假设我们所使用的断层扫描方法符合下述单调条件，即测量得到的相关性矩阵S和共享路径矩阵P 满足下述单调条件。

单调条件：对于所有的叶节点i，j，k，所测量到的相关性满足si，j＞sj，k＋δ（δ＞0），当且仅拓扑树的共享路径满足pi，j＞pj，k。

给定一组叶节点的随机顺序，选择一个叶节点（xi），并且获取这个叶节点和其它叶节点 （＝ ｛s1，2，s1，3，s1，4，…，s1，N｝）的成对相关性。其中，一些叶节点与xi有很高的相关性，另一些因为与xi只有较少的共享节点，所以具有较低的成对相关性。然后将这些相关性值进行排序，将具有较多共享节点的叶节点放置在一个集合中，将具有较少共享节点的叶节点放置在另一个集合中，我们将叶节点xi称为优势点，利用优势点得到偏序列，π：｛2，3，…，N｝→｛2，3，…，N｝（s1，πi≥s1，πi＋j，j≥1），但这个偏序不能被认为是DFS序列，如图2所示。

图2 利用一个叶节点所得到的偏序列

比较所划分的这些叶节点簇，簇与簇之间的相关性值相差一定的幅度δ，如图3 所示。然而，只使用一个优势点并不能估计出这些簇中节点的DFS序列。这只是利用其中一个叶节点与其它叶节点的相关性所判断得到的，因此，还需要另外一些节点的成对相关性才能正确的排序整个叶节点集合。从图3中可以看出，任何簇之间相关性都有一个δ的偏差，在 ｛CA，CB，CC｝这3个值中。在这3个簇的基础上正确排序这些叶节点，然后再排序这些子簇。利用相关性划分这些叶节点，划分成每个簇，然后在每个簇中重复这种探测过程，即运用子簇中新的优势点以及节点之间的成对相关性重新排序这些子簇中的节点。使用递归二分法减少了我们寻找叶节点DFS序列的难度。

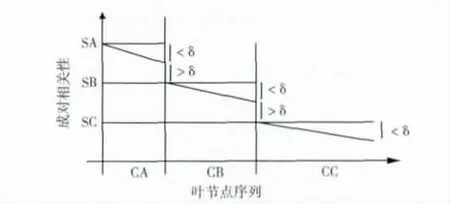
图3 不同叶节点簇之间的相关性差

对于给定边值δ的节点簇，使用这种二分法相对简单，只需排序相关性值并且找到所有可能的平分点。以节点x1为例，定义集合Ι，i∈Ι，如果到第i个偏序列πi与第i＋1个偏序列πi＋1之间的相似性大于δ，则说明这两个节点集合具有不同的父节点

平分的点即优势点，设为叶节点i＊，i＊∈Ι，这样叶节点被分为两个叶节点集合XA＝｛x1，xπ1，xπ2，…，xπi＊｝和

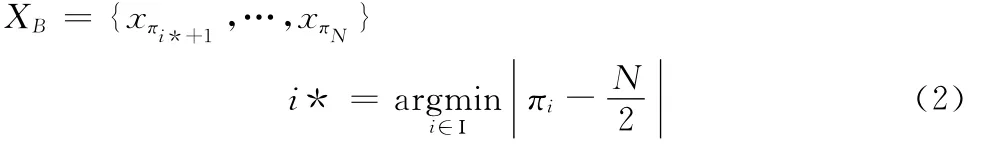
算法1：寻找叶节点DFS序列

（1）通过排队时延或时延协方差［5］找出叶节点x1与其它叶节点的相关性值，并列出成对相关性矩阵S。

（2）比较相关性值的大小，找出偏序列π：｛2，3，…，N｝→｛2，3，…，N｝。

（3）找出集合I＝｛i：s1，πi－s1，πi＋1≥δ｝

（4）找到评分点i＊，使用二分法，将叶节点集合X 划分 为 集 合XA＝｛x1，xπ1，…，xπi＊｝和XB＝｛xπi＊＋1，…，xπN－1｝。

使用上述迭代二分法可以成功找出叶节点的DFS 序列。利用叶节点的DFS序列，我们提出了下述DSTD 算法来推断网络拓扑结构。

2.2 DSTD算法推断逻辑拓扑

条件1：测量到的相关性矩阵S 和共享路径矩阵P 满足单调性条件，如果对于所有的叶节点i.j.k满足共享路径pi，j＞pj，k，那么所观测 到的相关性 满足si，j＞sj，k。

由命题1和条件1得到，相关性矩阵S和共享路径矩阵P的结构紧密相关。

命题2：给定一组叶节点 ｛x1，x2，…，xN｝的DFS序列，相关性矩阵满足单调条件，那么相关性矩阵将有以下属性

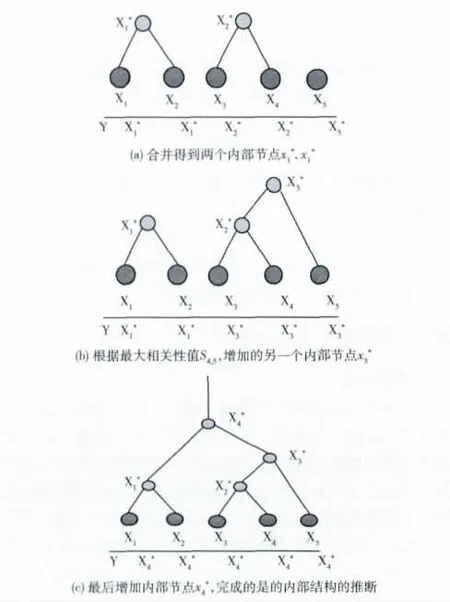
图4 DSTD 算法中合并每个叶子节点

定理 若叶节点DFS 序列和成对相关性满足单调条件，则只需要N－1 对探测包 （相关性值Si，i＋1，i＝ ｛1，2，…，N－1｝）来重构逻辑拓扑树。

证明：由单调条件可知，在一个子簇中，找到具有最大相关性值的一对叶节点，也就找到了具有最大共享路径的一对叶节点。对于N 各叶节来说，使用以往的方法获得所有需要的相关性值的数量级O（N2）。但是，在已获得叶节点的DFS序列和已知单调条件的情况下，只需要知道与叶节点xi（i＝｛1，2，…，N｝）直接相邻的两个叶节点xi－1和xi＋1之间的相关性值 （即si，i－1和si，i＋1需要）来推断出合理的拓扑结构。由命题2可知，对任意的j＞1，每个叶节点的相关性值si，i＋1＞si，i＋j，因此，与叶节点xi具有最大的共享路径的气体叶节点只能是与其相邻的xi＋1或xi－1。

算法2：描述

已知：利用算法1找到的叶节点的DFS序列X ＝｛x1，x2，…，xN｝，并列出叶节点的成对相关性值序列， ｛s1，2，s2，3，s3，4，…，sN－1，N｝

输入：拓扑树节点集，V ＝｛x1，x2，…，xN｝

树的边集，E ＝

重构拓扑树，T ＝（V，E）

边节点集，Y ＝｛x1，x2，…，xN｝

For k＝ ｛1，2，…，N－1｝

（1）找出

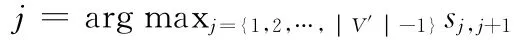
（3）创建新的内部节点，x＊

（4）将新的内部节点加入到节点集中，V ＝V ∪x＊

（5）加入新的边到新的内部节点，E＝E∪｛Yj，x＊｝∪｛Yj＋1｝

（6）参考旧的内部节点，找出边节点集，I ＝｛i：Yi＝Yjor Yj＋1｝

（7）更新边节点，Yi＝x＊for all i∈I

（8）更新相关性值，重复选择相关性值，设sj，j＋1＝0

输出：所估计的逻辑拓扑树结构，T。

3 仿真实验与性能分析

3.1 仿真实验

在不同大小的网络环境中，进行大量的仿真实验，用来比较本文算法与目前常用的聚类算法的探测数量。为了避免网络性能的不同所造成的偏差。实验是在无噪声的前提下进行，不同拓扑结构的每条链路的相关性值设为随机的，共享路径矩阵P均满足δ－Margin边距条件，且设定δ＝0.1。每个不同大小的网络所使用的最终数据均是由100个随机测量结果产生的。本实验采用紧接分组队的测量方法，采用时延协方差作为相关性参数。仿真结果对比图如图5所示，横坐标表示网络的大小，纵坐标表示拓扑推断中所需要的成对探测包的数量。由图5 可知，本文所提出的DSTD 算法所需要的成对探测包的数量低于目前常用的聚类算法的15%，很大程度的提高了拓扑推断的效率。

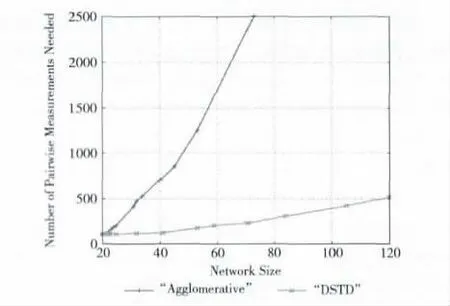
图5 DSTD 算法与传统聚类算法的探测量的比较

3.2 性能分析

在已知叶节点的DFS序列的情况下，只需要N－1数量的成对探测包，若未知叶节点的DFS序列，则需要pN log1N 数量的成对探测包，其中

证明：

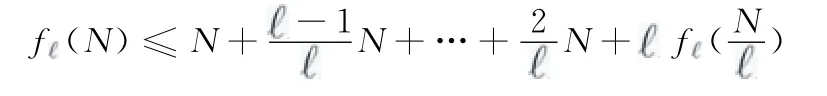
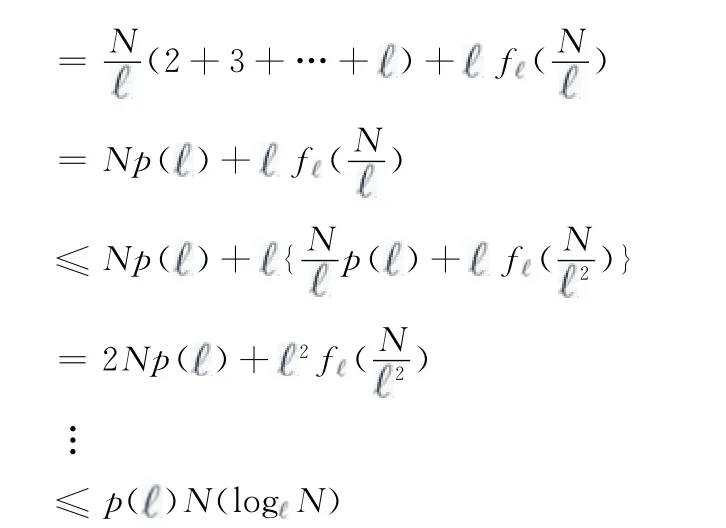
表1 聚类算法与DSTD 算法性能比较

4 结束语

本文提出的基于叶点DFS序列的DSTD 算法有效的减少了拓扑推断中所需的成对探测包的数量，提高了网络拓扑推断的效率，充分发挥了网络断层扫描技术不需要中间节点的协作的优势。通过计算和仿真实验证明，本算法需要的成对探测包的数量低于先前聚类算法需要的成对探测包数量的15%，有效的减少了测量流量，降低了因测量流量过大而造成的推断误差。

［1］ZHAO Honghua，CHEN Ming.Based tomography topology inference［J］.Computer Engineering，2009，35 （2）：92－95 （in Chinese）.［赵洪华，陈鸣.基于层析成像技术的拓扑推断［J］.计算机工程，2009，35 （2）：92－95.］

［2］WU Wenjia，ZHANG Jianzhong.Based on the measured end to end network topology inference algorithm ［J］.Journal of Xiamen University，2010，49 （1）：34－37 （in Chinese）. ［吴 文佳，张建中.基于端到端测量的网络拓扑推断算法研究 ［J］，厦门大学学报，2010，49 （1）：34－37.］

［3］Brian Eriksson，Gautam Dasarathy，Paul Barford，et al.Efficient network tomography for internet topology discovery ［J］.IEEE／ACM Transactions on Networking，2012，20 （3）：931－943.

［4］ZHAO Honghua，CHEN Ming.Topology inference based on tomography ［J］.Journal of Software，2010，21 （1）：133－146 （in Chinese）.［赵洪华，陈鸣.基于王网络层析成像技术的拓扑推断 ［J］，软件学报，2010，21 （1）：133－146.］

［5］ZHAO Honghua，HU Guyu，NI Guiqiang.A network topology inference algorithm based on 4－tupl packets measurement［J］.Journal of Beijing University of Posts and Telecommunications，2012，35 （2）：126－130 （in Chinese）. ［赵洪华，胡谷雨，倪桂强.基于四元分组测量的网络拓扑推断算法 ［J］.北京邮电大学学报，2012，35 （2）：126－130.］

［6］LI Guishan，CAI Wandong.Network link time delay distribution estimation method ［J］.Computer Engineering and Appli－cations，2009，45 （8）：21－28 （in Chinese）.［李贵山，蔡皖东.网络链路时延分布估计方法研究 ［J］.计算机工程与应用，2009，45 （8）：21－28.］

［7］Srinivas Gorur Shandilya，Marc Timme.Inferring network topology from complex dynamics ［J］.New Journal of Physics，2011 （13）：1－12.