基于六边形的无线传感器网络密钥管理方案
2014-12-23王小康李佩玥隋永新杨怀江
王小康,李佩玥,隋永新,杨怀江
(1.中国科学院 长春光学精密机械与物理研究所 应用光学国家重点实验室,吉林 长春130033;2.中国科学院大学,北京100049)
0 引 言
近年来,无线传感器网络[1](WSN)在各领域都发挥着日益重要的作用,有效的密钥管理[2]机制是WSN 进行安全通信的基础,因此密钥管理的研究对于WSN 的实际应用有着重要意义。
自Eschenauer和Glogor提出基于概率的E-G 方案[3]以来,许多类似的密钥管理方案如q-composite[4]、多密钥空间[5]、对称多项式[6]、组合设计理论[7]等方案相继被 提出。网络的连通性和安全性[8]是评定WSN 密钥管理方案的性能的两个主要标准。但是上述方案抵御敌手俘获节点攻击的能力并不强,例如对于Du等人的多密钥空间方案,当400个节点被捕获时,网络中受影响链路数达到100% (m=200,w=7,t=2);在Chan 等人的q-composite方案中,150个节点被俘获后 (q=1),网络受影响的链路就达到25%。为提高WSN 密钥分配方案的性能,Du等人将网格部署理论[9]应用到WSN 的密钥管理中,Du将网络划分为一系列的正方形网格,利用相邻分组间的密钥重叠因子[10]构建网络的连通性。Yu和Guan[11]改进了Du的方案,利用正六边形网格分组[12]增强了节点抵御攻击的能力。但这些方案抵御敌手选择性攻击的能力并不强,在Yu和Guan方案中,b=3,w=3时,敌手选择性的攻击某一网格,一旦俘获节点数目超过门限值,邻近的26 个网格密钥都会被攻陷。
为进一步改善WSN 的安全性能,本文利用网格部署理论将网络区域划分为两种类型的六边形网格,分组网格和密钥网格。每个分组网格中的节点利用多密钥空间方案建立密钥,而相同密钥网格中的节点则利用组合设计理论建立通信密钥。依据节点通信范围确定网格规模,使得只有相邻分组中的节点才能有效通信。模拟分析结果表明,相较于其它密钥管理方案,本方案的安全性更高。
1 相关方案回顾
1.1 多密钥空间方案
Du等人在E-G 和Blom 密钥分配的基础上提出了一种在WSN 中建立成对密钥的方案。在Blom 方案中,基站首先创建一个有限域GF (q)上的(λ+1)×N 阶的矩阵G,其中N 是网络节点数目。接着,基站创建一个有限域GF(q)上的(λ+1)×(λ+1)阶对称矩阵D,并计算A=(D×G)T。矩阵G 对全节点公开,其任意λ 列线性无关,矩阵D 则对各节点保密。由于D 是对称矩阵,K =A*G 也是对称矩阵,选取Kij=Kji作为节点i和j之间的通信密钥。可以通过如下操作实现该方案,对于节点k:①存储矩阵A的第k行;②存储矩阵G 的第k列。Blom 证明在不超过λ个节点被俘获时,攻击者无法恢复出矩阵D,网络密钥是安全的,一旦被俘获的节点数目超过λ,网络的安全性就会崩溃。为提高网络抗攻击的能力,Du,Deng 等人结合E-G 方案与Blom 方案,提出多密钥空间密钥预分配方案:每个节点从ω个对称矩阵中随机选择t个,两个节点如果共享对称矩阵D 则可以建立彼此间的密钥。与Blom 方案和E-G 方案相比,Du等人的方案抵御敌手俘获节点攻击的能力明显增强。
1.2 组合设计理论
Camtepe等人将组合设计理论应用于WSN 密钥预分配方案:假定网络的节点总数为N,用q 阶有限投影空间(finite projective plane)生成一个对称BIBD(q2+q+1,q+1,1),其中q是满足q2+q+1≥N 的素数。在该设计中,网络共生成q2+q+1个密钥,每个节点拥有q+1个密钥,其中任意两个节点共享一个密钥。在基于组合论的BIBD 方案中,网络的连通率为1。
1.3 基于节点部署理论的方案
Du等人将节点部署理论应用到密钥预分配中,将节点部署区域划分为一系列的网格,同一网格内的节点间,以及邻近网格内的节点间将以很大概率共享密钥,而相距较远的网格内的节点间共享密钥的概率很低。该方案不仅大幅度提高了网络的连通性,还有效地增强了无线传感器网络抵御敌手攻击的能力。
2 本文方案
本文以Liu等人的分组密钥预分配方案为基础上,结合多密钥空间方案和组合设计理论,提出一种新的基于正六边形部署的密钥管理方案。与Du等人的重叠因子方案不同,本文提出的方案将目标区域划分为两种网格,密钥网格和群组网格。如图1所示,每一个小六边形网格代表密钥网格,阴影区域的大六边形网格代表群组网格;每个群组网格包含一个完整的密钥网格和6 个 “半-密钥网格”,相邻的群组网格均分一个密钥网格。每个密钥网格和群组网格都有唯一的标识符。群组网格边长的选择依赖于节点的通信半径,假定群组网格边长为l,节点通信半径为r,为确保只有相邻群组网格内的节点才能进行通信,必须满足l≥2r。每个群组网格和密钥网格都拥有自己的密钥池,不同网格之间的密钥池交集为空集。每个密钥网格利用组合设计理论BIBD(q2+q+1,q+1,1)构建自身的密钥池,每个群组网格内的节点利用多密钥空间方案建立通信密钥。

图1 群组网格与密钥网格的划分
2.1 密钥预分配
假定目标区域被划分为m 个群组网格,则有4m 个密钥网格。节点在每个密钥网格内均匀分布,每个密钥网格内有Nc个节点。用二维参量(i,j)(i=1,2…4 m,j=1,2…,m)来唯一地表征一个网格区域,其中i代表所属密钥网格的标志号,j代表所属群组网格的标志号。具体步骤如下:
(1)基站生成4 m 个BIBD(q2+q+1,q+1,1)密钥池,分别定义标识符k(k=1,2,…,4 m)。每个密钥池包含q2+q+1个密钥,组合成q2+q+1组,每组包含q+1个密钥且任意两组共享一个密钥,其中q是满足q2+q+1≥Nc的最小素数。
(2)基站生成有限域GF(q)上的(λ+1)×Nm(Nm≥4 Nc)阶的矩阵G,G 的任意λ 列线性无关。
(3)基站生成m 组对称矩阵,每组包含w 个Nm阶对称矩阵D1,D2,…,Dw,并分别计算Ai=(Di×G)T。矩阵G 对网络公开,矩阵Di对各节点保密。
(4)将所有节点 (假定总数为N)划分为4m 组,每组赋予标识符l(l=1,2…,4 m)。选取密钥池l的q2+q+1组密钥中的Nc组分别赋予每个节点。
(5)基站从第j(j=1,2…,m)组对称矩阵组生成的矩阵A1,A2,…,Aw中随机选取t个,并将矩阵Ai的第k行赋予群组网格j中标识符为k(k=1,2,…,4 Nc)的节点。
2.2 共享密钥的发现
每个节点用一个三维向量(i,j,k)(i=1,2…4 m,j=1,2…,m,k=1,2,…,4 Nc)来唯一地表征。其中,i代表节点所处的密钥网格标志号,j代表节点所处的群组网格标志号,k代表在群组网格中节点的ID。部署完成后,每个节点广播其三维序列号(i,j,k),同时接收邻居节点广播的序列号。假定节点A(i1,j1,k1)与节点B(i2,j2,k2)是邻居节点,A,B之间的密钥建立分为如下情形:①若j1=j2,A,B处于同一群组网格中。A,B检查彼此是否共享对称矩阵Di,若二者共享至少一个对称矩阵,则能够建立成对密钥;②j1≠j2,i1=i2,A,B处于同一密钥网格,不同的群组网格,依据BIBD(q2+q+1)的性质,A,B以概率1共享一对密钥;③若j1≠j2,i1≠i2,A,B不在同一密钥网格,也不在同一群组网格中。A,B无法直接建立共享密钥,与基于栅格的密钥预分配方案类似,A,B通过路径查找建立共享密钥。可以通过调整网格的大小来减小这类链路,当l=2r时,这类链路的比例仅为5%,因此在下文的分析中忽略这类链路。
3 方案性能分析
3.1 局域连通率
局域连通率plocal的定义参见文献 [9]。假定ni,nj是WSN中两个传感器节点;事件A(ni,nj)表示节点ni,nj是邻居节点;事件B(ni,nj)表示二者共享密钥或密钥空间,则局域连通率为
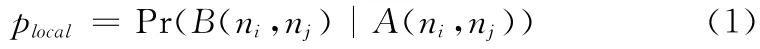
3.1.1 组内链路与组间链路
为计算网络中任意两节点ni,nj之间的连通率,需计算组间链路与组内链路的比例。组间链路是指处于不同群组网格内的节点之间的链路,组内链路是指同一群组网格内节点构建的链路。


随机节点A 的组间链路所占比例近似为

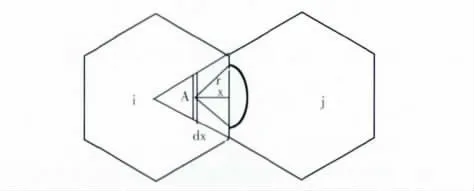
图2 组间链路的比例
3.1.2 局域连接率


3.2 网络安全性分析
无线传感器网络的安全性是由x 个节点被敌手俘获后受影响的链路的百分比来表征的。但是对于基于部署理论的方案而言,情况稍有复杂:攻击者可以随机地从网络中俘获若干节点,也可以针对性地从某一网格俘获节点。本文讨论两种情形,局域安全性和全局安全性。局域安全性是指一个群组网格中x 个节点被俘获后对链路造成的影响,全局安全性是指整个网络中的x 个节点被俘获后对网络链路的影响。
如果x 个节点被俘获,将会有3种受影响的链路:①直接被俘获节点相关的链路;②俘获x 个节点后,敌手中能够攻陷的间接的组内链路;③俘获x 个节点后,敌手中能够攻陷的间接的组间链路。假定网络共N 个节点,每个节点周围有d 个邻居节点,敌手俘获x 个节点,则受影响的链路的比例为
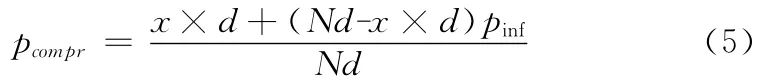
其中,pinf是敌手俘获x 个节点后能够攻陷间接链路的概率。
3.2.1 局域安全性分析
假定每个群组网格内有Nm个节点,其中x 个节点被敌手俘获,则受影响的链路计算如下:
直接相连的链路n1=xd/2敌手间接攻陷的组内链路

敌手间接攻陷的组间链路

因此局域链路的安全性可以用式 (6)表示

3.2.2 全局安全性分析
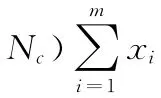
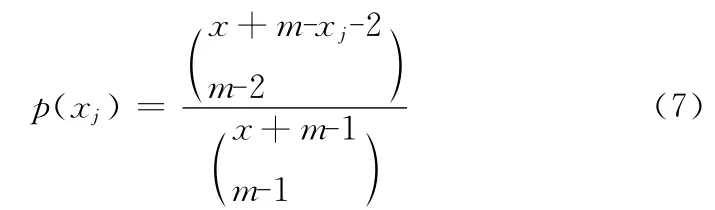
考虑到各个群组网格节点被俘获个数相互独立,全局安全性pgsec可以用式 (8)表示
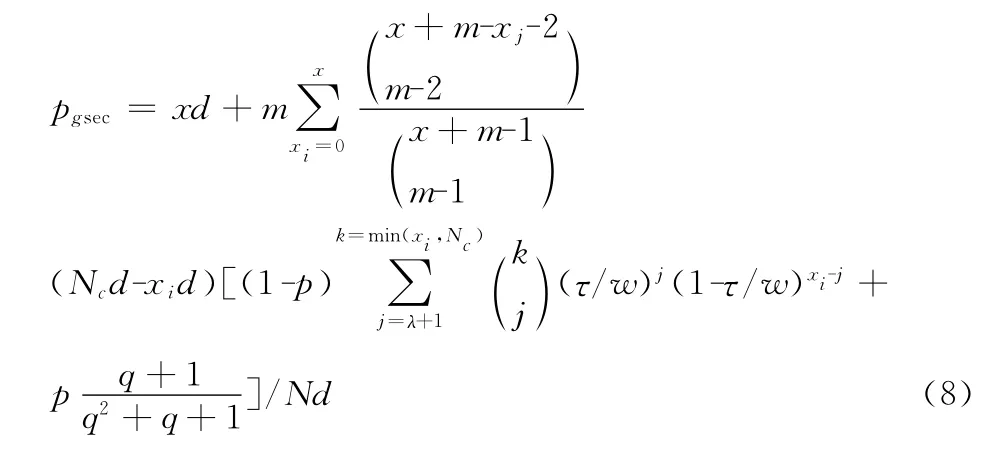
4 仿真模拟分析
4.1 场景建立
假定N 个节点 (N=10000)均匀部署在1000mⅹ1000m 的区域内,每个节点的通信半径为r=40m,并拥有50个邻居节点。选取全局连通率Pc=0.9999。由上述参数可以计算出网络深度d=18,门限连通率prequired=0.36。选取群组网格六边形边长l=80m,部署区域共有m=64个群组网格。每个群组网格包含156个节点,每个密钥网格包含39个节点,选取q=7。为了更好地与不同方案进行比较,我们假定每个节点的最大存储空间为200。
4.2 本地连通率的模拟
网络的本地连通性为plocal=(1-p)×p1+p×1,当l=2r时p=0.2034。每个节点的存储容量为M=200,故t*(λ+1)+(q+1)=200。该方案与Du等人的多密钥空间方案的本地连通率的比较如图3所示。
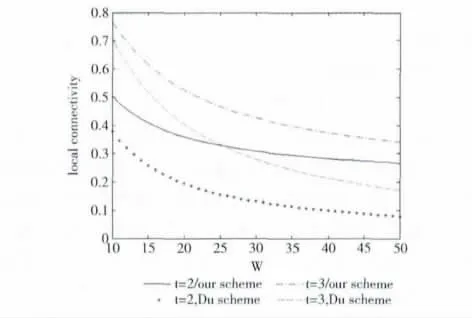
图3 不同t对应的本地连接率
为满足plocal≥prequired,我们需要t=2时w ≤17,t=3时w ≤42。本方案的本地连通率在0.5到0.8之间。一个很高的一跳连通率并不是必需的,因为Deng等人提出的多跳路径查找可以有效地增强节点间的连通率。
4.3 安全性模拟
4.3.1 局域安全性模拟
本文通过一个群组网格中的x 个节点被俘获后对网络链路的影响来研究不同方案的局域安全性。模拟中各参量见表1,其中N 代表节点总数,sf 代表部署面积,Pc是全局连通率,r是节点的广播半径,l是六边形网格边长,m 是节点最大存储容量,λ是门限值。

表1 模拟过程中各项参量
本方案与Yu,Guan等人方案的局域安全性的比较如图4所示。在Yu等人的方案中,俘获节点数未达到门限值时,链路受影响的比率近似线性增加,但是一旦节点数超过门限值,整个网格的密钥就完全被敌手破解;在本方案中,每个网格节点数目不足以使敌手破解一个密钥空间(w=10,t=2时,大约需要攻陷400个节点才能破解一组密钥空间,但每个群组网格仅有156个节点)。
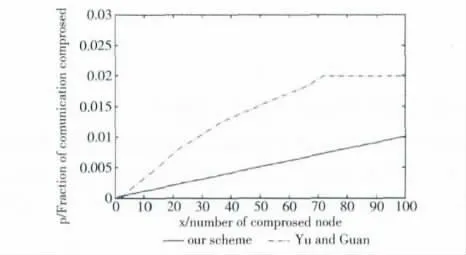
图4 局域安全性的模拟
4.3.2 全局安全性模拟
不同方案的全局安全性的比较如图5所示。图中 “Du deployment”指Du 等人的部署理论方案, “Basic scheme”指多密钥空间方案。在本方案和多密钥空间方案中选取m=200,t=2;Du等人的部署理论中,S=100000,m=46,因为较小的m 能够增强网络抗攻击的能力。图5显示我们的方案相较于其它几种密钥管理机制有着更强的安全性。当少于400个节点被俘获时,该方案与多密钥空间方案性能类似,二者都优于Du的部署方案。但是超过2.5%的节点被俘获后,该方案的优越性开始体现。当1000个节点被俘获后,受影响的链路仅为12%,即使考虑到计算过程中p的误差,受影响的链路也不会超过20%。

图5 全局安全性模拟
5 结束语
本文结合部署理论,多密钥空间方案和组合设计理论,提出了一种新的无线传感器网络密钥管理方案。其核心思想是将节点部署区域划分为两种类型的六边形网格,不同网格内的节点采用不同的方式建立密钥。理论分析和仿真结果表明,该方案不仅能够有效地抵御敌手攻击尤其是选择性攻击,还能维持较高的网络连通率。在传感器节点存储空间有限的情形下,本方案支持的网络规模更大,更适用于大规模部署的无线传感器网络。
[1]Stankovic J A.Wireless sensor networks [J].Computer,2008,41 (10):92-95.
[2]Barati A,Dehghan M,Barati H,et al.Key management mechanisms in wireless sensor networks [C]//SENSORCOMM,2008:81-86.
[3]Manivannan D,Neelamegam P.WSN:Key issues in key management schemes-A review [J].Research Journal of Applied Science,Engineering and Technology,2012,4 (18):3188-3200.
[4]Xiaomin G W L.Research and improvement for q-composite key management scheme [J].Electronic Measurement Technology,2010,33 (6):37.
[5]Zhang J,Varadharajan V.Wireless sensor network key management survey and taxonomy[J].Journal of Network and Computer Applications,2010,33 (2):63-75.
[6]Fanian A,Berenjkoub M.An efficient end to end key establishment protocol for wireless sensor networks[C]//9th International ISC Conference on Information Security and Cryptology,2012:73-79.
[7]Brubaker B,Bump D,Friedberg S.Weyl group multiple dirichlet series:Type a combinatorial theory (AM-175)[M].Princeton University Press,2011:201-232.
[8]SU Zhong,LIN Chuang,FENG Fujun.Key management schemes and protocols for wireless sensor networks[J].Journal of Software,2007,18 (5):1218-1231 (in Chinese).[苏忠,林闯,封富君.无线传感器网络密钥管理的方案和协议 [J].软件学报,2007,18 (5):1218-1231.]
[9]Liu D,Ning P,Du W.Group-based key predistribution for wireless sensor networks [J].ACM Transactions on Sensor Networks,2008,4 (2):11.
[10]YAN Xueli,YE Xiaohui.Random key predistribution scheme for sensor networks based on hexagon deployment model[J].Application Research of Computers,2012,29 (4):1457-1461 (in Chinese).[严雪莉,叶晓慧.一种基于六边形部署模型的面向传感器网络的随机密钥预分配方案 [J].计算机应用研究,2012,29 (4):1457-1461.]
[11]Yu Z,Guan Y.A key management scheme using deployment knowledge for wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems,2008,19 (10):1411-1425.
[12]DAI Hangyang,XU Hongbing.Key management in sensor network based on hexagon grid deployment model[J].Journal of Electronic Measurement and Instrument,2008,22(5):48-52 (in Chinese).[代航阳,徐红兵.基于六边形网格部署模型的传感器网络密钥管理 [J].电子测量与仪器学报,2008,22 (5):48-52.]
