基于邻居向量的近似子图匹配

陈 东，王 波，席耀一，唐浩浩

（信息工程大学 信息系统工程学院，河南 郑州450001）

0 引 言

作为图数据挖掘［1－4］的一个重要研究内容，近似子图匹配在很多领域都有应用，如蛋白质交互网络查询［5］、犯罪团伙检测［6］、专家推荐系统等。对于大型网络的近似子图匹配有多种相似性度量标准。TALE 算法［7］以边丢失为度量标准，通过构建混合索引结构降低候选节点的规模，提高查询速度，但准确性不高。SA－Index算法［8］要求节点和边存在对应关系，该算法基于结构与节点标签对数据图进行划分，缩小了路径搜索的空间，再将边／路径构成图，运算效率比TALE算法有所提高。也有学者针对一些应用对结构相似性要求低的特点 （如知识网络的语义相似查询）提出了新的相似度度量标准，并采用新方法提高运算效率。Ness算法［9］通过查询图和数据图相应节点k－近邻的标签相似对候选节点进行过滤，再验证过滤后的节点。NeMa算法［10］考虑节点的邻近度，引入邻居向量的概念，提出了子图匹配代价度量图匹配的相似性，采用一种启发式推理算法进行子图匹配，比Ness算法有更高的节点准确率和召回率。Ness和NeMa算法得到查询节点和匹配节点的对应关系，以节点准确率和召回率作为度量标准，但由于没有充分利用结构信息，忽略了查询边和匹配边的对应关系。

本文研究以下问题：给定一个大型数据图和一个查询图，在数据图中找到和查询图相似的子图。针对NeMa算法运算效率高但没有考虑边对应关系的问题，进行以下改进：①根据查询节点在查询图中的重要程度给查询节点赋予权重，并改进匹配代价和迭代推理算法；②通过节点过滤降低候选节点的数量；③改进NeMa算法在节点匹配优化阶段起始节点的选择；④通过边匹配得到边的对应关系。

基于以上4点改进，本文提出近似子图匹配算法IMNeMa（important node network match），该 算 法 不 仅 得 到节点对应关系，还得到边对应关系。算法首先对查询节点的匹配节点进行过滤得到候选节点，然后改进匹配代价和迭代推理得到匹配节点集合，最后通过边匹配得到匹配图。

1 预备知识

标签图：标签图是一个节点有标签标注的网络图，表示为G＝ （V，E，L，f），其中，V 表示图的节点集合，E表示图的边集合，L 表示节点的标签集合，f 是标签分配函数V→L，表示节点到标签的映射，f（u）∈L表示节点u∈V的标签（如社会网络的标签可以是人的职业、兴趣等）。

问题描述：给定数据图G＝ （VG，EG，LG，fG），查询图Q＝ （VQ，EQ，LQ，fQ），要求找到数据图中满足式（1）的子图GT

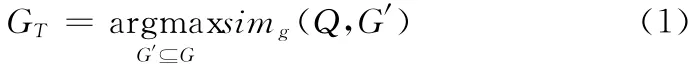
真实网络由于结构复杂，并且存在噪声和数据丢失，拓扑结构完全相同的子图有时并不存在，因此需要进行近似子图匹配。图的近似匹配有很多种度量标准，其中，p同态［11］是由Fan等在图同态定义基础上的改进，允许节点标签相似以及边和路径的对应，更加适合真实网络。本文图的相似定义simg（Q，G′）与p 同态类似，若存在VQ到V′的一个映射关系g：VQ→V′，且满足如下2个条件，则认为Q 和G′相似：

其中，g（u）和g（v）表示u 和v 在G′中的对应节点，p（g（u），g（v））＝｛（g（u），u1），...，（ui，g（v））｝表示g（u）到g（v）的最短路径。

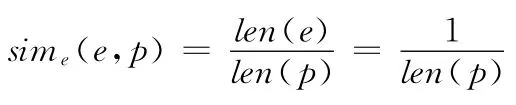
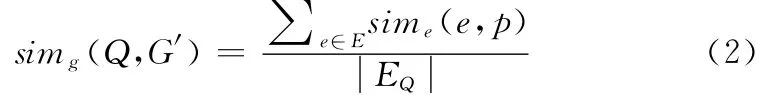
当对于Q 的每一条边，G′都有一条边对应时，simg（Q，G′）＝1。

2 IMNeMa算法

本文将近似子图匹配分为节点过滤、节点匹配和边匹配3个主要阶段。首先通过节点过滤得到候选节点集合，其次利用节点匹配得到匹配节点的位置，最后在包含匹配节点的扩展图中进行边匹配。

2.1 节点过滤

仅通过节点标签相等得到查询节点的候选节点集合，会造成集合中有大量错误匹配的候选节点，导致节点匹配阶段的运算量增大，因此需要通过节点过滤对候选节点集合进行删减。如果一个匹配图和查询图同构，那么对应节点度则相同，但在本文近似匹配的定义下，由于允许若干个等价查询节点 （标签相同，在查询图中的位置也相同）对应一个匹配节点，一些 “好”候选节点的度也会小于对应的查询节点度，因此通过匹配节点度大于等于查询节点度进行节点过滤会过滤掉一些 “好”候选节点。为了解决这个问题，本文引入节点邻接标签度。

定义1 节点邻接标签度：节点邻接标签度是指节点的邻接节点集合中的不同标签的数量。LN（v）表示节点邻接节点的标签集合，那么表示节点邻接标签度。使用节点邻接标签度，将节点度的比较转化为邻接节点集合标签种类的比较。

如果查询图和匹配图相似度为1，则匹配图中每个节点的邻接标签度和相应查询节点的邻接标签度相同，而匹配图又是数据图的子图，因此数据图中 “好”候选节点的节点标签度要大于对应查询节点的节点标签度。考虑到复杂网络的无标度分布特性［12］，数据图中会有大量节点度很小的节点，其节点邻接标签度也很小，采用节点邻接标签度进行过滤，可以将候选节点集合精简，尽可能的保留 “好”候选节点，减少了节点匹配不必要的计算。

给定数据图G 和查询图Q，对G 中节点进行规则过滤，得到每个查询节点的候选节点集合M（v）。过滤规则如下

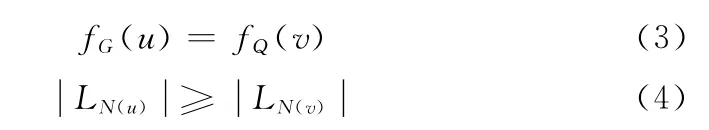
式 （3）表示u和v 标签相同。式 （4）表示u的节点邻接标签度大于v 的节点邻接标签度。通过节点过滤，得到查询节点的候选节点集合M（v）。

2.2 节点匹配

节点匹配的目的是得到匹配节点在数据图中的位置。NeMa算法能得到节点的对应关系，但在数据图标签稀疏情况下运算时间长、准确率低 （将在实验部分说明）。真实网络环境复杂，有的网络标签密度较为稀疏，并且很多应用要求保持匹配节点的连接关系［11］，这就造成NeMa算法难以直接应用到节点匹配。

节点匹配阶段基于NeMa算法进行以下改进：①根据查询节点在查询图中的重要程度给查询节点赋予权重，并改进匹配代价和迭代推理算法；②改进NeMa算法在节点匹配优化过程起始节点的选择。通过以上两点改进，提高了节点匹配的匹配效果和运算效率。

NeMa算法将节点的h－邻居节点向量化，定义了匹配代价，通过匹配代价得到匹配节点，但是NeMa算法不重视结构在匹配中的作用，无法得到准确的匹配节点。本文改进并重新定义了匹配代价，改进后的匹配代价能返回更准确的匹配节点。首先介绍节点匹配阶段用到的定义。

定义2 h－邻居节点集合：h－邻居节点集合N（v）表示图中所有与v的距离 （即最短路径长度）小于或等于h 的节点构成的集合。

定义3 邻居向量：节点u 的邻居向量RG（）u ＝｛＜u′，PG（u ，u′）＞ ｝，其 中，u′ 是u 的h－邻 居 节 点，PGu，（ ）u′ 表示u′到u 的邻近度

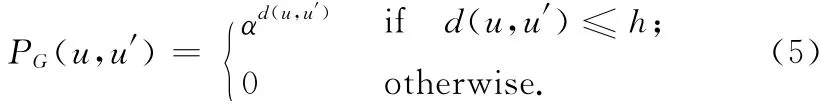
式中：d（u，u′）——u′到u的距离（即最短路径长度），传播因子0＜α＜1，h＞0表示向量化节点u的半径（范围），由于2个实体间的关系随着距离的增加迅速下降，h的取值通常很小，本文取h＝2［10］。接下来利用邻居向量计算匹配代价。

定义4 单节点匹配代价：给定一个节点匹配函数，查询节点v和匹配节点u＝（v）的单节点匹配代价F（v，u）为

定义5 节点权重：引入节点权重w（v）表示节点在图中的重要性。本文用节点度衡量。即节点的度越大，该节点越重要。节点权重也可以采用其他算法度量，如节点度、特征向量中心度等。

定义6 全节点匹配代价：给定一个节点匹配函数表示查询节点v∈VQ到匹配节点u∈VG的映射，则全节点匹配代价定义为

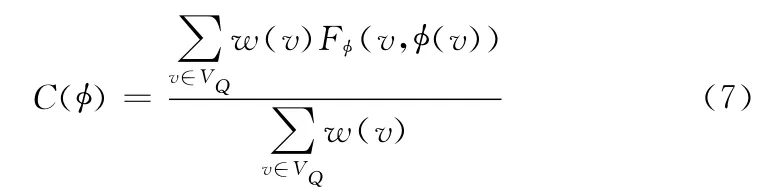
式中：w（v）——节点权重，0≤C（）≤1。本文通过使用节点权重对单节点匹配代价加权，使节点匹配代价更能反映查询图的结构特性。由于在查询图中，不同的节点具有不同的重要性，而重要节点对图匹配具有重要意义，即全节点匹配代价对重要性不同的节点的匹配代价敏感程度不同，式 （7）中加入了节点权重，使全节点匹配代价对重要节点的匹配代价更加敏感。这里认为全节点匹配代价越小，得到的匹配图与查询图越相似。如果匹配图和查询图同构，则全节点匹配代价为0，反之不一定成立。全节点匹配代价是节点匹配的度量标准。

2.2.1 IMNeMaInfer算法

NeMaInfer算法 （NeMa算法的子算法）是一种基于图模型最大和推理问题的启发式迭代推理算法，目的是得到查询节点的匹配节点集合，使子图匹配代价最小。IMNeMaInfer算法对NeMaInfer算法进行改进，在迭代推理时加入节点权重提高收敛速度，并在节点匹配优化时选择邻接标签度大的节点作为初始节点。通过节点过滤得到候选集合M（v）后，先初始化推理代价函数U0（v，u），迭代计算每个查询节点v和其候选集合M（v）中每个候选节点的推理代价函数Ui（v，u），然后更新最优匹配Oi（v）。每次迭代过程中，记录最优匹配节点u 的邻居匹配节点。当保持不变的最优匹配节点比例达到某个阈值时，迭代终止。最后，通过节点匹配优化选择理想的起始节点，再向周围扩展，获得节点匹配集合Φ。算法流程如下：

IMNeMaInfer算法

输入：数据图G＝ （VG，EG，LG，fG），查询图Q＝（VQ，EQ，LQ，fQ），查询节点候选集M（v）

输出：Q 的节点匹配集合Ф

IMNeMaInfer算法基于推理代价和最优匹配提高每次迭代中查询节点的匹配质量。

定义7 推理代价：在迭代过程中，推理代价定义为

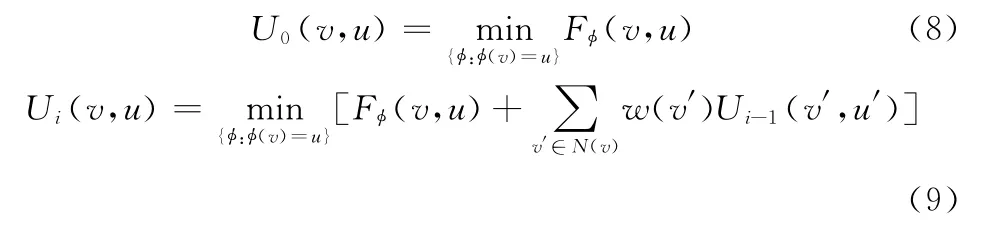
假定i＞0，u＝（v），u′＝（v′）。推理代价是单节点匹配代价F（v，u）和v的所有h－邻居节点v′在上次迭代中推理代价的加权和，加权权重是节点权重。在推理过程中加入节点权重，这就使推理代价相同而权重不同的查询节点对推理产生不同的作用，使推理过程更快收敛。

定义8 最优匹配：每次迭代中，定义每个查询节点的最优匹配。查询节点v的最优匹配定义为

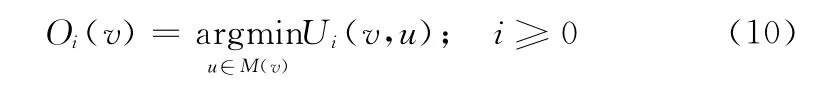
由于不能保证节点匹配算法在一定次数的迭代后收敛，因此当满足条件Oi（v）＝Oi－1（v）的节点比例达到阈值ε时终止迭代。

节点匹配优化：迭代终止时每个查询节点的最优匹配不一定满足全节点匹配代价最小，因此需要对迭代结果进一步处理。Φ（v）表示查询节点v的最大可能匹配节点 （the most probable match）。在每次迭代过程中，记录匹配节点的h－邻居节点中匹配部分 （算法第9行）。节点匹配优化过程：首先，选择邻接标签度最大的查询节点v 作为起始节点，v的最大可能匹配节点

式中：i＝i′表示最终迭代。其次，其他的查询节点的最大可能匹配节点通过扩展得到。比如v 的h－邻居节点v′∈N（v）的最大可能匹配Φ（v′）可利用Φ（v）得到

2.2.2 算法优化

推理代价Ui（v，u）的计算具有指数级的时间复杂度。NeMa算法引入子推理代价，使推理代价计算能够在多项式时间内完成。在此需证明IMNeMa算法迭代过程加入节点权重后依然成立。

定义9 子推理代价：子推理代价定义如下

式中：η（v）＝［∑v′∈N（v）PQ（v，v′）］－1。定理1 推理代价Ui（v，u）计算式为

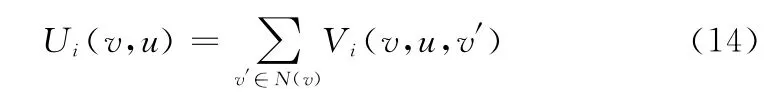
证明

通过定理1，计算Ui（v，u）只需计算Vi（v，u，v′），故可以在多项式时间计算完成。

2.2.3 时间复杂度

2.2.4 孤立候选节点和索引建立

定义10 孤立候选节点：孤立候选节点定义为

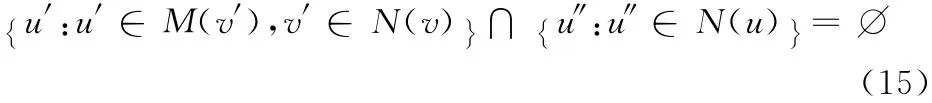
该式表示u的h－邻居节点和v 的任何一个h－邻居节点的候选节点交集为空，这里定义为孤立候选节点，否则为非孤立候选节点。孤立候选节点用来进一步过滤候选集中的节点。

索引建立：为了快速计算推理代价①在离线索引阶段，计算数据图的每个节点u的邻居向量RG（）u 、节点邻接标签度和标签权重并且存储成索引文件；②在在线节点匹配阶段，如果u 被选为查询节点v 的候选节点，验证u 是否是一个孤立候选节点，如果是，将其从v的候选集中去除。

2.3 边匹配

在得到匹配节点后，需要知道节点之间的连接关系。SA－Index等算法［8］是先确定最短路径搜索的方法获得每条查询边的匹配边，最后通过贪心算法将匹配边连接成匹配图。这种直接选定2个节点进行最短路径搜索的处理方式，搜索空间大，并且在查询节点候选节点数多的情况下搜索次数多。这里通过节点匹配得到查询节点的匹配节点集合后，利用邻居向量索引得到匹配节点集合构成的匹配扩展图，在扩展图中通过最短路径算法，返回查询边的匹配边集合，减少了搜索的空间和搜索次数，降低了时间复杂度。边匹配EdgeMatch算法描述如下：

EdgeMatch算法

输入：节点匹配集合Ф，查询边集合EQ

输出：匹配图GT

（1）利用邻居向量索引得到匹配节点的γ（h）－邻居节点，和Ф 共同构成匹配扩展图Ga＝ （Va，Ea，La，fa）

（2）初始化VT＝Ф，ET＝

（3）for each（v，v′）∈EQdo

（4） 在Ga中求path（（v），（v′））

（5）ET＝ET∪path（（v），（v′）），VT＝VT∪S

（6）得到匹配图GT

算法复杂度 假设匹配节点的最大度为d，算法第1行利用邻居向量索引得到匹配扩展图Ga的时间复杂度为第4行采用广度优先搜索算法求最短路径，匹配路径的数量为，则搜索算法的时间复杂度为。故EdgeMatch算法时间复杂度为

以上IMNeMa算法是得到相似度最大的匹配图，很多应用要求得到和查询图最相似的k 个图，此时，需要先将式 （1）修改为返回与节点v最相似的k 个，然后对这k 个候选节点进行节点匹配优化得到k 组匹配节点集合Ф，最后分别进行边匹配即可。

2.4 算法复杂度比较

将IMNeMa算法和同样能得到边对应关系的近似子图匹配算法SA－Index做复杂度比较 （已知运算效率SA－Index＞Tale，SA－Index＞G－Ray）［8］。SA－Index 算 法 复 杂 度 为为查询边的数量，mQ是一个查询节点候选节点的最大值，分别为数据图的节点数和边数，为候选路径集合的大小。IMNeMa算法主要分为节点过滤、节点匹配、边匹配3个阶段，每阶段的时间复杂度分别为。由于IM－NeMa算法中节点过滤和边匹配运行时间远小于节点匹配运行时间，因此IMNeMa算法运行时间主要由节点匹配阶段决定，时间复杂度约为表示数据图中标签种类，l表示数据图中一个标签对应的最大节点数，dQ表示一个查询节点的h－邻居节点的最大数目，比较如下（对于一个边数确定的连通图，；真实网络中往往小于故a1。所以，IMNeMa算法在运算效率上要优于SA－Index算法。

3 实验结果及分析

实 验 环 境：Pentium （R）Dual－Core E5500＠2.80 GHz，8.00 GB 内 存，操 作 系 统 为Ubuntu12.04 LTS 64位，编译环境为gcc／g＋＋。实验使用了Patents，wiki－Talk，Youtube这3个数据集。Patents和wiki－Talk数据来自Stanford大学大型网络数据集。Patents是美国37 年专利数据集，节点表示专利，边表示专利之间的引用关系，标签是专利的类型；wiki－Talk数据集是有向图，节点表示维基用户，边表示用户之间的关系，对数据图进行处理，将有向图变成无向图。Youtube社会网络关系数据集中，节点代表用户，边代表用户间的关系。wiki－Talk 和Youtube数据集节点标签由人工生成，人工生成的虚拟标签在网络中均匀分布。处理后的数据集的详细统计信息见表1。

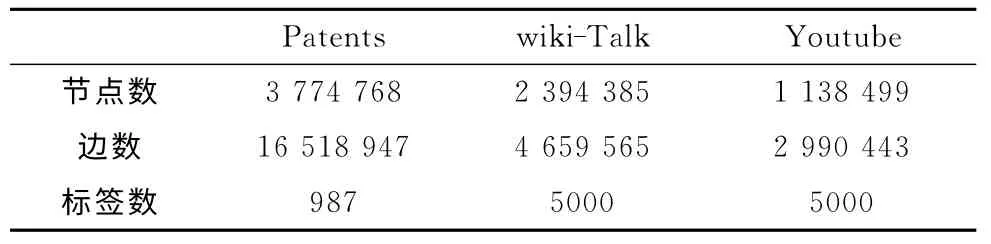
表1 数据集信息统计

3.1 相似度指标的评测实验及分析

真实网络标签密度差异较大，比如知识网络的节点标签密度接近1，而蛋白质网络的标签密度为10%左右，而论文引用网络更是达到0.5%左右。因此，首先比较IMNeMa算法、NeMa算法和NeMaexact算法在不同标签密度下子图匹配的相似度。NeMa算法是得到查询图的匹配节点集合，而IMNeMa还要求得到匹配边集合；并且NeMa算法在节点匹配优化时随机选择起始节点，效果较差。为了使实验结果更有说服力，本文实验中提到的NeMa算法都是进行了改进，即节点匹配优化时选择节点邻接标签度大的节点作为起始节点，得到节点匹配后进行边匹配。Ne－Maexact算法则对NeMa算法进行四点改进：①加入节点过滤；②对匹配代价和IMNeMa保持一致；③节点匹配优化时选择节点邻接标签度大的查询节点作为起始节点；④节点匹配后进行边匹配。由于本文要求边匹配，数据图中可能有多个子图和查询图匹配，因此考虑节点准确率和召回率［10］不能客观反映匹配效果。该实验选择的评价标准为simg（Q，G′）（详见式 （2））。对3种算法建立h ＝2的邻居向量索引；ε＝0.8；k＝1即top－1匹配。数据图选择wiki－Talk数据集，分别通过人工生成不同标签密度的标签集合并均匀分配给节点。查询图是数据图随机产生的子图，和分别为11，10，每个标签密度下产生20个查询图，对结果求平均。实验结果如图1所示。

从图1可以看出，当标签密度大于10%时，3 个算法都有较好的性能，但随着标签密度的下降，3 个算法的性能也随之下降，而IMNeMa算法下降趋势缓慢。这说明IMNeMa算法的适用范围更广，匹配结果更准确。原因有两点：①节点过滤将不满足要求的节点从候选集合中去除，减少了对匹配过程的干扰；②IMNeMa算法在迭代过程中加入了节点权重，对查询图的不同节点在迭代中的作用起到了很好的区分作用，避免了匹配较多错误的节点，从而更好的保持了匹配图的结构。

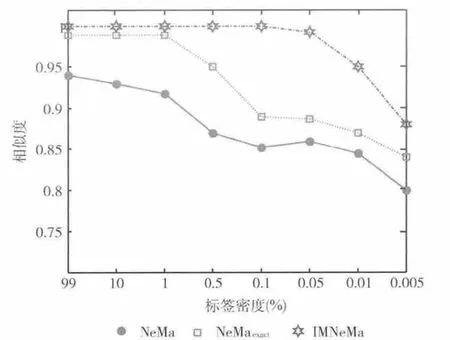
图1 不同标签密度下的相似度

通过实验发现，3 种算法对于星形结构匹配都具有很好的效果，相似度维持在0.95以上，但对线性结构匹配效果波动较大，以标签密度为0.01%的数据集为例，线性结构进行子图匹配的相似度最低达到了0.5。这是因为本文采用的是启发式算法，节点匹配优化的起始节点的匹配是否准确对实验结果产生很大影响，如果选择了错误的起始节点，匹配相似度就会比较低。而起始节点匹配是否理想是由所选节点的特征决定的。邻接标签度大的节点特征多，找到正确起始节点的概率大。所以星形结构要比线性结构匹配效果好，这也是节点匹配优化时选择邻接标签度大大的节点作为起始节点的原因。社会网络中存在连接紧密且直径较小的核心结构，并且规模中等的社区主要呈现星形结构［12］，说明IMNeMa 算法能应用到社会网络的子图匹配。

从图2可以看出，随着噪声的增加，子图匹配相似度在下降，但是不同数据集下的下降速度不同。这是由查询图的选择和数据集的结构和标签的差异导致。该算法在噪声率较高的情况下仍有较好的表现，这说明该算法有很好的容错性。

3.2 运算效率指标的评测实验及分析

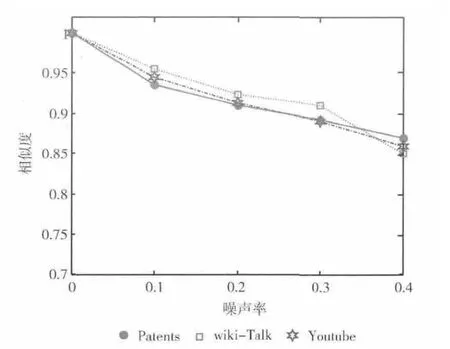
图2 不同噪声率的相似度

比较IMNeMa算法、NeMa算法、NeMaexact算法的在3种不同情况给下的运算效率。3个算法情况及参数设定同上，查询图生成方法同上。在wiki－Talk数据集中考察不同标签密度情况下的运算时间，查询图大小同上，实验结果如图3所示；在Youtube数据集中考察不同算法不同数据图节点数时的子图匹配时间，查询图大小同上。实验结果如图4所示；在Patents数据集中考察不同数量查询节点和查询边的情况下的子图匹配时间，查询节点和查询边的数量关系满足实验结果如图5所示。

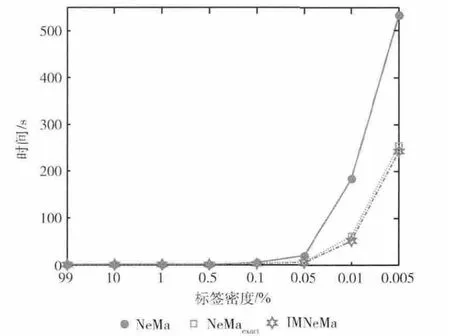
图3 不同标签密度下IMNeMa的运算效率 （WIKI－talk）

图4 不同节点数量下的运算效率 （Youtube）

图5 不同查询图大小的运算效率 （patents）

从图3、图4和图5可以看出，随着标签密度的下降或数据集规模的增大或查询图的增大，IMNeMa算法和Ne－Ma算法查询时间都在增加，这是由于查询节点候选集变大，造成初始化式 （8）的计算量和迭代次数的增加。相比NeMa算法，IMNeMa算法通过节点过滤降低候选集，迭代过程中引入节点权重使迭代收敛更快，因此运算效率更高。Patents数据集下运算时间长，这是因为标签密度低，造成候选节点集合大，迭代推理计算量增大。

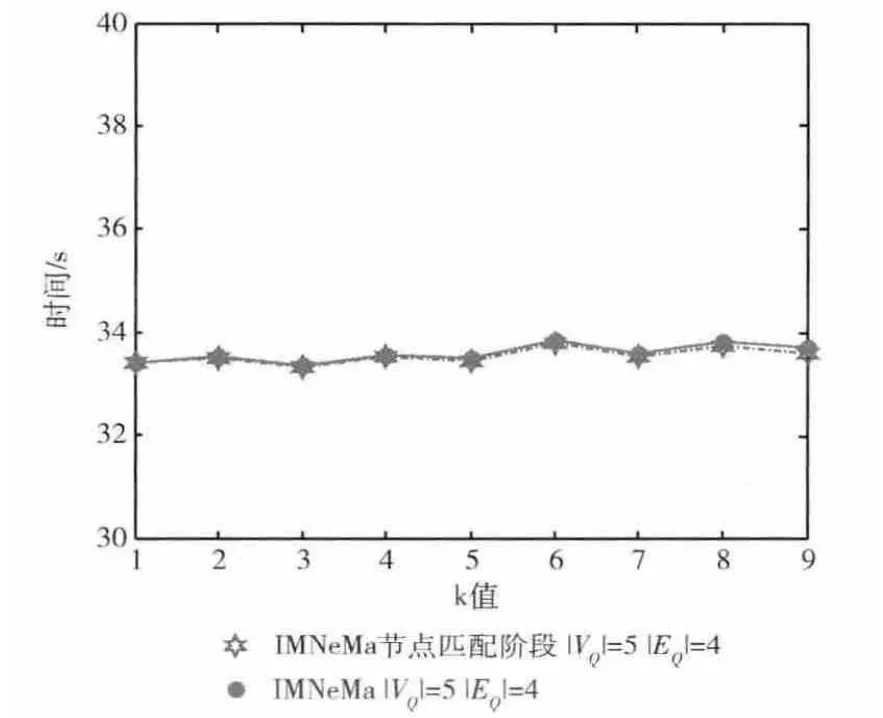
图6 Top－k近似匹配运算效率 （patents）

3.3 基于IMNeMa算法的Top－k近似匹配实验

考察IMNeMa top－k 近似匹配在不同k 值下的运算效率。实验数据选择Patents数据集，查询图的节点数为5，边数为4。实验结果如图6所示。从图中可以看出：在返回top－k近似匹配结果时，IMNeMa算法节点匹配阶段的运算时间基本保持平稳，这是因为该算法主要是初始化和迭代推理计算复杂，节点匹配优化部分和边匹配耗时相对较小。

4 结束语

本文基于邻居向量提出了IMNeMa算法应用于近似子图匹配，可以得到数据图中和查询图最相似的k 个匹配图。实验证明，该算法在标签较稀疏和噪声存在的情况下都有较高的匹配效果。由于采用先节点匹配后边匹配的思路，边匹配的耗时被大大降低，在百万节点的数据图中也保持较高的相似度和较高的运算效率。节点匹配优化时的起始节点选择不佳会造成节点匹配的效果降低，标签稀疏图中的候选集合数量大，分别对匹配效果和运算效率造成影响，有待进一步解决。

［1］Han Jiawei.Mining heterogeneous information networks by exploring the power of links ［C］／／Discovery Science.Berlin：Springer Berlin Heidelberg，2009：13－30.

［2］Zou L，Mo J，Chen L，et al.gStore：Answering SPARQL queries via subgraph matching ［J］.Proceedings of the VLDB Endowment，2011，4 （8）：482－493.

［3］Han L，Finin T，Joshi A.GoRelations：An intuitive query system for DBpedia ［M］.The Semantic Web.Berlin：Springer Berlin Heidelberg，2012：334－341.

［4］Sambhoos K，Nagi R，Sudit M，et al.Enhancements to high level data fusion using graph matching and state space search［J］.Information Fusion，2010，11 （4）：351－364.

［5］Zaslavskiy M，Bach F，Vert JP.Global alignment of proteinprotein interaction networks by graph matching methods ［J］.Bioinformatics，2009，25 （12）：1259－1267.

［6］Chau P.Catching bad guys with graph mining ［J］.XRDS：Crossroads，The ACM Magazine for Students，2011，17 （3）：16－18.

［7］Tian Y，Patel JM.Tale：A tool for approximate large graph matching ［C］／／IEEE 24th International Conference on Data Engineering.IEEE，2008：963－972.

［8］Zhu L，Keong Ng W，Cheng J.Structure and attribute index for approximate graph matching in large graphs［J］.Information Systems，2011，36 （6）：958－972.

［9］Khan A，Li N，Yan X，et al.Neighborhood based fast graph search in large networks［C］／／Proceedings of the ACM SIGMOD International Conference on Management of Data.ACM，2011：901－912.

［10］Khan A，Wu Y，Aggarwal CC，et al.NeMa：fast graph search with label similarity ［C］／／Proceedings of the 39th International Conference on Very Large Data Bases.VLDB Endowment，2013：181－192.

［11］Fan W，Li J，Ma S，et al.Graph homomorphism revisited for graph matching ［J］.Proceedings of the VLDB Endowment，2010，3 （1－2）：1161－1172.

［12］DOU Binglin，LI Shusong，ZHANG Shiyong.Social network analysis based on structure ［J］.Journal of Computers，2012，35 （4）：741－753 （in Chinese）. ［窦炳琳，李澍淞，张世永.基于结构的社会网络分析 ［J］.计算机学报，2012，35 （4）：741－753.］