未知环境下基于椭圆约束的机器人路径规划
2014-12-23张琴丽吴怀宇
张琴丽,吴怀宇,陈 洋
(武汉科技大学 信息科学与工程学院,湖北 武汉430081)
0 引 言
目前,路径规划主要分为对已知环境路径规划和对未知环境路径规划。在已知环境中进行路径规划的方法已经比较成熟,如:人工势场法[1,2]、A*算法[3]、遗传算法[4]等。在未知环境中,由于机器人无法准确判断环境中是否有障碍物存在及障碍物的具体位置信息,只能通过传感器获知其探测范围内的环境信息来进行局部的路径规划。因此,环境信息的不完整性是未知环境中路径规划的关键问题[5]。
近年来,很多学者针对未知环境下的机器人路径规划做了大量研究,并取得了一定成果[2-10]。其中具有代表性的成果是将多种规划方法相结合来进行混合路径规划。如文献 [6]中提出的利用Voronoi图和势场法对未知环境进行路径规划。该方法采用两级规划算法:顶层规划采用广义Voronoi图法产生从起始点到目标点的路径;底层规划采用势场法对未知障碍物进行避障。该方法有效解决了有大量障碍物存在的未知环境下机器人路径规划问题。但该方法主要适用于大量密集型障碍物环境中的路径规划,算法复杂度高、花费时间长。为解决算法复杂度问题,有学者提出一种基于椭圆约束的机器人导航 (ellipsoidal constrained agent navigation,ECAN)算法[8]。该算法的主要思想是通过规划具有相关约束的椭圆来寻找机器人运动路径,将机器人路径规划问题转换为椭圆优化的问题。该方法能有效应用于2维和3维的未知环境,且具有路径规划实时性高、复杂度低等优点。但是机器人在规划过程中,未考虑机器人运动角度且未检测到障碍物对规划椭圆的影响,易使机器人陷入局部震荡,从而导致规划失败。
针对上述研究现状及不足,本文通过引入机器人运动步长及运动方向的约束,根据凸二次约束二次优化[7]理论,建立具有凸约束的目标函数模型,有效解决了ECAN 算法中机器人目标不可达问题,并且大幅提高了算法的收敛速度,降低了复杂度和规划时间。使用该方法能够快速准确地在未知环境下进行路径规划。
1 问题描述
设机器人在二维平面的有限区域内运动,该区域内任意分布着有限个障碍物。路径规划的任务是在障碍物信息未知的情况下,机器人规划出一条从起始点S到目标点G与障碍物无碰撞的路径。本文提出的基于椭圆约束的路径规划方法,将障碍物与机器人统一等效为点。规划的基本原理如图1所示。

图1 椭圆约束路径规划基本原理
设机器人的起始位置是S(0,0),目标位置是G(4,1)。环境中障碍物信息如图1 (a)所示。机器人在运动过程中,当运动到坐标(1,1)时,通过激光传感器扫描检测到在坐标(2.2,1)处存在一个障碍物。此时,机器人根据运动的当前位置,检测到的障碍物位置以及目标点的位置,规划出一个满足一定约束条件的椭圆,并且确定机器人在该椭圆内与障碍物无碰撞的运动方向,如图1 (b)所示。当机器人在椭圆内运动到指定位置时,又检测到坐标(3.5,2)处存在另一障碍物。机器人则根据当前检测到的信息规划出满足约束条件的另一个椭圆。此时目标点在该规划椭圆的边界上,机器人直接从当前位置运动到目标位置,完成路径规划,如图1 (c)所示。
根据上述路径规划的基本原理,在障碍物信息未知的二维环境内,进行无碰撞路径规划可分为三步:
(1)机器人在检测到障碍物存在的t时刻,规划满足一定约束条件的椭圆;
(2)确定机器人在该椭圆内的运动方向;
(3)计算机器人在该椭圆内运动方向上的运动距离。
上述过程需要求解满足凸二次约束的二次优化[7]问题。假设机器人通过激光传感器扫描,检测到有限区域内环境障碍物信息,将该区域称为机器人视野域。视野域由激光扫描参数(r,θ)决定,其中r∈(0,R],θ∈[-,]。t时刻,机器人、障碍物及目标点信息分别由坐标,和xg表 示; 规 划 的 椭 圆 方 程 表 示 为 Φt(P,q,r) =,即椭圆内部满足intΦt={x|Φt(P,q,r)<0} ,椭圆边界值满足。其中P 为二维正定矩阵,
1.1 椭圆约束的路径规划模型
机器人运动过程中,在t时刻检测到有障碍物存在,则规划出满足以下约束条件的椭圆:①机器人在椭圆内;②所检测到的障碍物在椭圆外;③目标点在椭圆边界上或在椭圆外。满足这3个约束条件的数学模型为
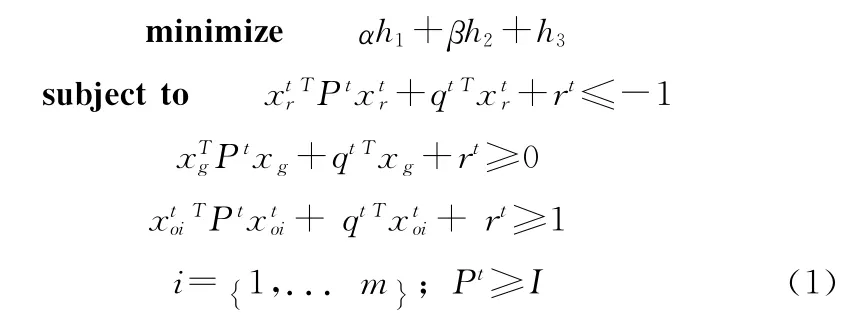
为了保证机器人能够保持向目标位置运动,所规划的椭圆要尽量靠近目标点。式 (1)中数学模型的目标函数h1最小化机器人当前位置离椭圆边界的距离;目标函数h2保证在障碍物存在的情况下,所规划的椭圆最大;目标函数h3表示目标点离椭圆圆心的距离,保证在满足约束的情况下椭圆离目标点最近,当目标点在椭圆边界时,h3为零。
1.2 机器人运动方向模型
t时刻规划出可行椭圆后,机器人在椭圆内的运动必须选择合适的方向使机器人在向目标点运动的同时避开障碍物。本文采用椭圆的特征向量和特征值及代数几何的方法,计算机器人在椭圆内部的运动方向xn。
若目标点在椭圆边界上,即满足Φt(xg)=0,椭圆内部机器人运动方向xn为当前位置指向目标位置的单位向量;若目标点在椭圆外,即Φt(xg)>0,则根据以下方法计算出椭圆内机器人的运动方向。
(1)建立椭圆坐标系:定义椭圆的长短轴分别为矩阵P 最大最小特征值所对应的特征向量xp,xo。xo在与xp成±90°的方向。若xp方向左侧障碍物的数量多于右侧障碍物的数量,则xo选择为矢量xp的-90°方向;反之,xo选择为矢量xp的+90°方向。
(2)判断目标点与椭圆x 轴的位置关系,确定椭圆内机器人的运动方向
设t时刻椭圆圆心为C(xtc,ytc),目标点坐标G(xg,yg),机器人坐标R(xtr,ytr)。根据式 (2)判断目标点与椭圆x 轴的位置关系

若l≥0,则目标点位于椭圆x轴左侧,如图2 (a)所示。根据式 (3)、式 (4)求椭圆上一点B(xb,yb)
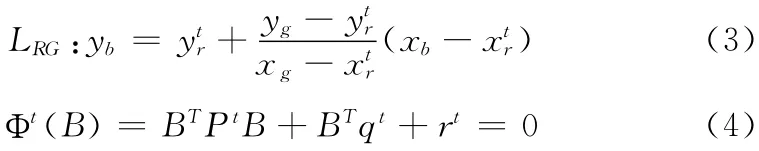
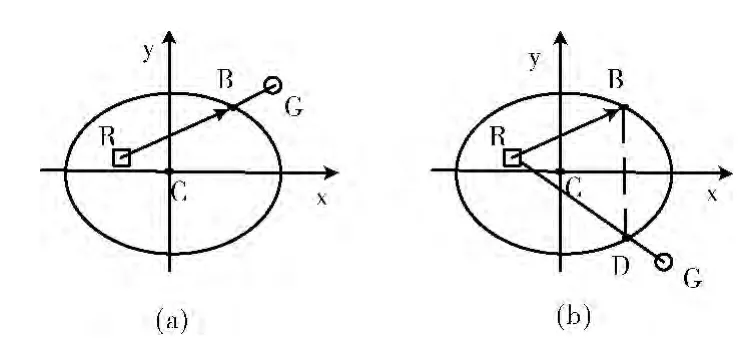
图2 椭圆内机器人运动方向
1.3 机器人在椭圆内的运动步长
计算出椭圆内机器人的运动方向xn,则机器人沿该方向的运动步长ln=min(δ1,δ2),其中δ1是根据机器人的运动速度给定的一个标量值,若目标点在椭圆上,则δ2=,若目标点在椭圆外,则
1.4 具有椭圆约束的路径规划算法
机器人路径规划算法主要步骤可描述如下:
步骤1 初始化相关变量α,β,γ;初始化机器人的起始点及目标点;初始化激光所扫描的二维有限区域范围;
步骤2 如果机器人未到达目标点 (与目标点的距离大于0.01m),执行步骤3;否则判断机器人已到达目标位置,执行步骤9;
步骤3 在激光传感器扫描的二维环境范围内,根据式(1)规划满足约束条件的椭圆;
步骤4 如果目标点位于步骤3中所规划的椭圆之外时,执行步骤5;否则执行步骤6;
步骤5 根据式(2)、式(3)、式(4)求椭圆上一点B;
步骤6 计算机器人在椭圆内的运动方向xn;
步骤7 计算机器人沿椭圆内运动方向上的运动步长ln=min(δ1,δ2);
步骤8 机器人按照上述规划路径运动,并不断更新机器人的位置信息;返回步骤2重复执行。
步骤9 输出机器人的运动轨迹。
2 仿真实验及分析
利用凸优化工具箱CVX[7]在Matlab环境下进行仿真实验。仿真中,基本参数设置如下:α=0.1,β=5×10-5,γ=1,r=2m,θ=120°。首先利用本文算法在复杂未知环境下得到路径规划结果,然后将其与文献 [8]中已有方法进行比较。
2.1 未知环境中的仿真
根据本文提出的算法进行路径规划。设置仿真实验环境为10m×10m 的区域,并随机生成静态障碍物坐标。机器人起始位置s(2,1),目标位置G(8,6)。路径规划仿真结果及每次椭圆规划所需时间如图3、图4所示。

图3 本文算法路径规划仿真结果
由图3分析可知,利用该算法在障碍物未知的环境中进行路径规划,能够使机器人避开障碍物,到达目标点。在规划过程中,机器人根据检测到的当前环境信息所规划的椭圆选择运动步长,通过控制机器人每次规划运动的长度和方向来寻找正确的路径。该算法在障碍物未知的情况下,能够快速进行路径规划,减少规划时间(如图4 所示),提高了机器人路径规划的有效性和实时性。
2.2 算法对比研究
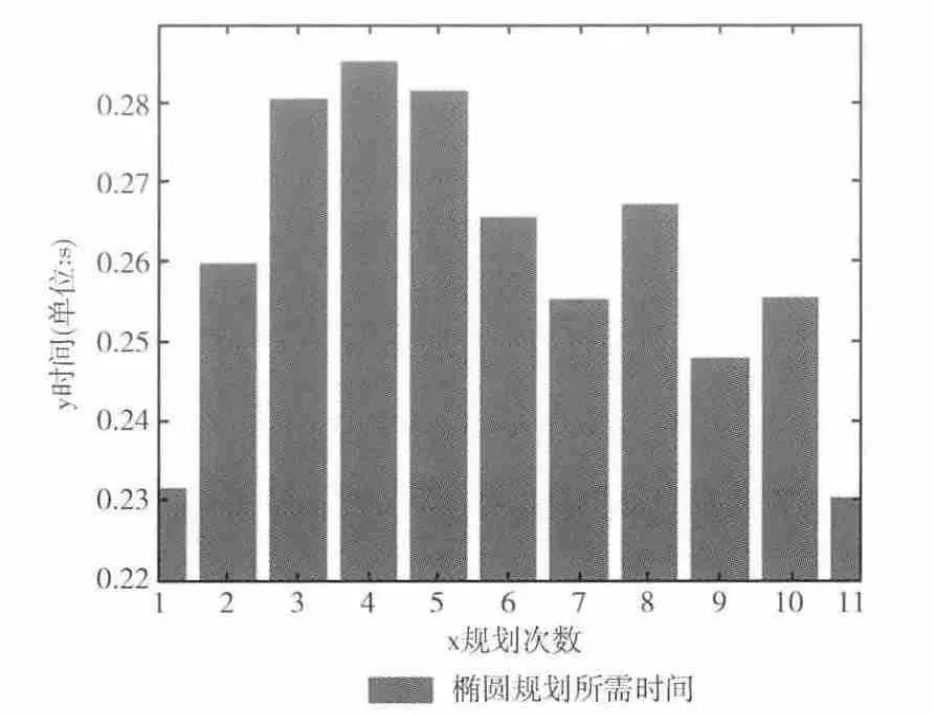
图4 椭圆规划所需时间
将本文提出的算法与文献 [8]中提出的ECAN 算法进行对比分析。分别用2种不同的算法进行路径规划,观察规划结果。主要进行两方面的对比。第一方面比较机器人是否顺利到达目标点,第二方面比较在利用2种算法都能到达目标点的情况下,所规划路径的优劣情况。
2.2.1 算法性能的对比
设置仿真实验环境为10m×10m 的区域,随机生成静态障碍物坐标。机器人初始位置s(0,0),目标位置G(9,9)。分别采用本文算法和ECAN 算法进行路径规划,规划结果如图5所示。
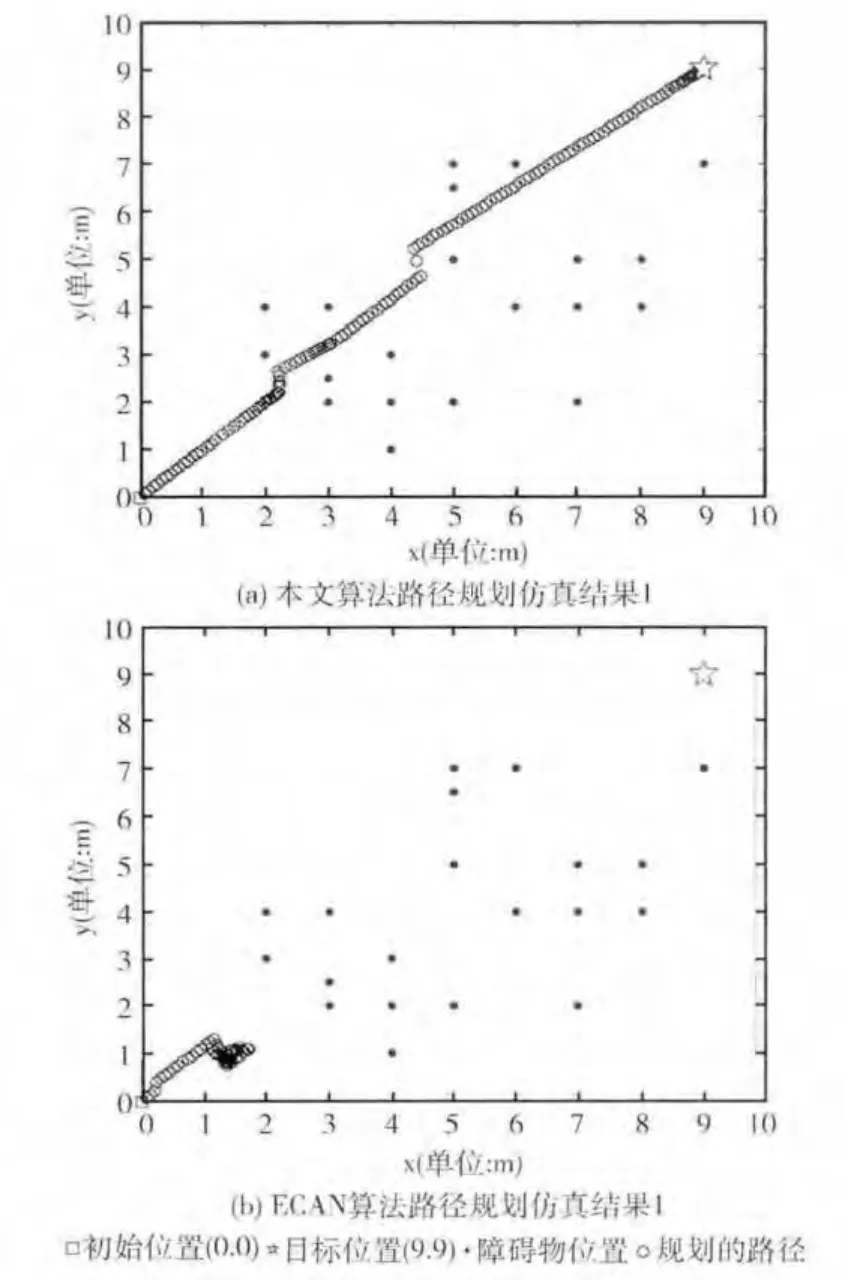
图5 不同算法仿真结果对比
由图5知,使用ECAN 算法时,机器人在复杂环境中规划路径容易陷入局部震荡的情况,从而导致机器人路径规划失败 (如图5 (b)所示)。本文所提出的改进算法能有效解决规划过程中机器人陷入局部震荡,目标不可达的问题 (如图5 (a)所示)。
为了进一步验证该算法解决局部震荡问题的有效性,分别使用该算法和文献 [8]中的算法进行路径规划100次,将规划成功次数进行对比分析。随机设置100 个二维有限区域,随机生成静态障碍物点。对每个区域分别用2种不同的算法进行路径规划,记录每种算法成功次数。对比实验结果见表1。
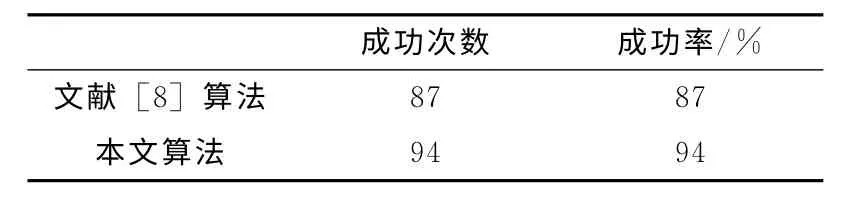
表1 路径规划成功率
由表1可知,本文提出的算法规划成功次数要高于文献 [8]中所提出的算法规划成功次数。对文献 [8]算法在障碍物密集环境下路径规划存在的目标不可达问题,本文提出的算法有很好的规划效果。该算法对复杂环境的适应性更高。
2.2.2 规划的路径对比
在2种算法均能规划成功时,比较所规划路径的优劣情况。仿真实验环境为10m×10m 随机生成障碍物坐标的区域。机器人起始位置s(0,0),目标位置G(8,6)。2种算法进行规划的规划结果如图6所示。
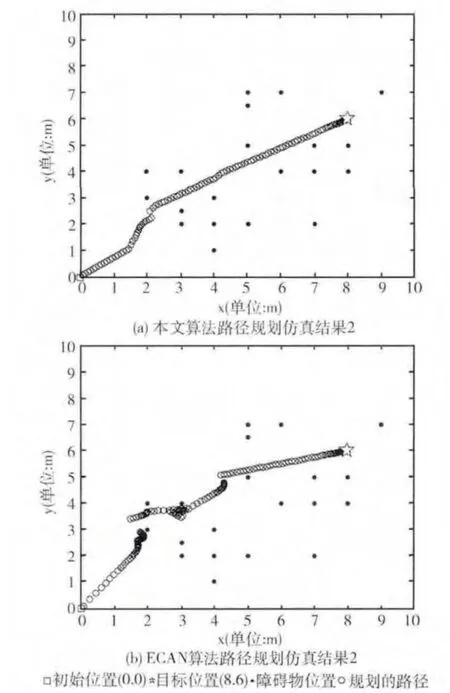
图6 不同算法规划成功路径的优劣对比
在均能规划正确路径到达指定的目标点,并且完成避障行为的情况下,本文提出的算法所规划的路径 (图6 (a)所示)要比ECAN 算法 (图6 (b)所示)所规划的路径长度更短,连续性更好,路径更平滑。本文所提出的基于ECAN 的改进算法可在线运行,实时规划路径,对于障碍物未知的环境,具有很好的环境适应能力。采用该算法能快速有效的在未知环境下规划出平滑的,无碰撞路径。
3 结束语
本文提出了一种未知环境下基于椭圆约束的移动机器人路径规划算法。该算法提高了复杂环境下移动机器人避障规划的能力,在规划路径时,引入机器人运动步长及运动方向的约束,有效的提高了算法的规划效率,提高了路径规划的成功率。利用凸优化理论的数学建模方法进行路径规划,与以往利用智能算法进行路径规划相比,不需要经过多次反复迭代来寻找最优解,其建立的数学模型即为最优解模型。当环境规模较大,机器人对复杂环境中障碍物的信息一无所知时,该算法具有很强的自适应能力,和其他算法相比,更能体现其优越性。在机器人的实际应用中也有很好的发展前景。
[1]LI G,Tamura Y,Yamashita A,et al.Effective improved artificial potential field-based regression search method for autonomous mobile robot path planning [J].International Journal of Mechatronics and Automation,2013,3 (3):141-170.
[2]ZHU Yi,ZHANG Tao,SONG Jingyan.Path planning for nonholonomic mobile robots using artificial potential field method [J].Control Theory & Applications,2010,27 (2):152-158 (in Chinese).[朱毅,张涛,宋靖雁.非完整移动机器人的人工势场法路径规划 [J].控制理论与应用,2010,27(2):152-158.]
[3]ZENG C,ZHANG Q,WEI X.GA-based global path planning for mobile robot employing A* algorithm [J].Journal of Computers,2012,7 (2):470-474.
[4]Ismail ALT,Sheta A,AL-Weshah M.A mobile robot path planning using genetic algorithm in static environment [J].Journal of Computer Science,2008,4 (4):341-344.
[5]HU Jun,ZHU Qingbao.Path planning of robot for unknown environment based on prior knowledge rolling Q-leaning [J].Control and Decision,2010,25 (9):1364-1368 (in Chinese).[胡俊,朱庆保.未知环境下基于有先验知识的滚动Q学习机器人路径规划 [J].控制与决策,2010,25 (9):1364-1368.]
[6]OK K,Ansari S,Gallagher B,et al.Path planning with uncertainty:Voronoi uncertainty fields[C]//IEEE International Conference on Robotics and Automation,2013:4596-4601.
[7]Boyd SP,Vandenberghe L.Convex optimization [M].U.K:Cambridge University Press,2004.
[8]Sharma S.QCQP-tunneling:Ellipsoidal constrained agent navigation[C]//Proceedings of the 2nd IASTED International Conference on Robotics Robo.Calgary:Acta Press,2011:294-301.
[9]CHEN Xiong,ZHAO Yilu,HAN Jianda.An improved ant colony optimization algorithm for robotic path planning[J].Control Theory &Applications,2010,27 (6):821-825 (in Chinese). [陈雄,赵一路,韩建达.一种改进的机器人路径规划的蚁群算法[J].控制理论与应用,2010,27 (6):821-825.]
[10]KANG Liang,ZHAO Chunxia,GUO Jianhui.Improved path planning based on rapidly-exploring random tree for mobile robot in unknown environment[J].Pattern Recognition and Artificial Intelligence,2009,22 (3):337-343 (in Chinese). [康亮,赵春霞,郭剑辉.未知环境下改进的基于RRT 算法的移动机器人路径规划 [J].模式识别与人工智能,2009,22 (3):337-343.]
