基于变长聚类的多敏感属性概率k－匿名算法

唐印浒，钟 诚

（广西大学 计算机与电子信息学院，广西 南宁530004）

0 引 言

平衡隐私保护和数据可用性之间的矛盾是数据发布中隐私保护研究的一个关键问题。文献 ［1］改进传统k－匿名（k－anonymity）算法以抵御同质性攻击、提高数据集安全性，加速了匿名过程。文献 ［2］提出p＋－敏感k－匿名模型，使得除了满足k－匿名之外，每个等价类内敏感属性的不同种类数至少为p，但该模型仍然存在k－匿名本身具有的不足。文献 ［3］对l－多样性 （l－diversity）模型进行改进，提出了 （l，α）－多样性模型，该模型除了要求满足l－多样性外，还要求每个等价类中敏感属性值的权值之和至少为α。文献 ［4］提出一种基于聚类的敏感属性l－多样性匿名化算法，该算法生成的每个聚类至少有l个不同的敏感属性值，每个聚类的大小介于l和2l－1之间，以达到优化划分并提高数据安全性。然而，l－多样性模型并没有解决背景知识攻击问题。

为了解决上述方法存在的不足，一些学者将统计泄露控制 （statistical disclosure control）技术中的微聚集［5，6］方法引入到数据表的k－匿名化中。针对数值型数据集，文献［7］提出了一个基于聚类的定长微聚集算法。在保证组内方差之和最小的前提下，文献 ［8］提出了聚类时间短的微聚集算法。文献 ［9］提出了概率k－匿名模型，该模型在确保能获得与k－匿名一样匿名效果的前提下，不要求类内必须至少有k个相同的准标识符属性值。

本文在文献 ［9］的基础上，引入记录的权重值，建立了依据距离和权值选择聚类种子的模型，设计实现基于变长聚类的概率k－匿名算法，在不降低隐私保护程度的前提下，以提高匿名数据集的可用性；设计实现融合k－means与变长聚类算法的概率k－匿名算法，以解决算法在处理大数据集时耗时长的问题。

1 基于改进变长聚类的概率k－匿名算法

1.1 聚类种子选取模型

在基于聚类的k－匿名算法中，聚类种子记录的选择对于聚类结果数据的质量、数据可用性的影响是非常大的。聚类种子记录的选择方式的不同，将会产生不同的聚类效果。

在变长聚类V－MDAV 算法中，每次循环聚类时V－MDAV算法选择的都是距离整个数据集质心最远的记录作为下一个类的种子记录进行聚类。该算法在选择种子时只考虑了记录与质心之间的距离这个因素，它将所有记录平等地看待，最后聚类完成后剩余记录中很可能存在一些用户期望优先得到发布但没有被发布的记录，这对于用户来说，发布的匿名数据集的数据可用性必然低于其期望值。

为此，除了考虑距离之外，本文在选择聚类种子的时候，还综合考虑了种子记录的权重值这个因素。我们定义了选择因子概念，作为变长聚类算法选择种子记录的依据，选择因子的计算

其中，选择因子表示某个记录在被选择作为种子进行聚类时的决定参数，距离表示该记录距数据集质心的距离，权重值 （取值范围：0～1）表示用户期望该记录被优先发布出来的程度，权重值越大，表明用户对该记录被优先发布的期望值越大。

1.2 匿名化算法

本文提出的基于改进变长聚类的概率k－匿名算法W－VMDAV 的主要思想是：给定一个有n个记录的数据集D 及其权重值集W 和匿名参数k，首先计算所有记录的选择因子并据此选取一个选择因子最大的记录作为第一个类的聚类种子，在剩余记录中选取k－1个距离该种子记录最近的记录加入该类，并对这个类进行扩展，直到该类大小在［k，2k－1）范围内或者没有记录能加入这个类时结束。以此类推，重复上述步骤建立下一个聚类。聚类过程结束后，对于剩余记录，将它们加入到距离最近的类中。最后，对所有类实施交换操作以实现匿名化。

匿名数据集的数据质量采用文献 ［9］所定义的聚类前后数据集内各自相关系数之间差值的绝对值的平均值来衡量。聚类前后数据集内各自相关系数之间差值的绝对值的平均值越接近于零，说明聚类后匿名数据集的数据质量越高，数据可用性越高。

算法1：W－V－MDAV 算法

输入：原始数据集D，权重值集W，匿名参数k

输出：匿名数据集T

Begin

（1）计算距离矩阵，存储数据集D 中两两记录之间的距离；

（2）计算原始数据集D 的质心；

（3）计算所有记录的选择因子；

（4）while剩余记录数remaining＞k－1do

Begin

1）根据剩余记录的选择因子选取一个记录作为聚类种子；

2）从剩余记录中选择距离聚类种子最近的k－1个记录，生成类cluster；

3）若剩余记录中某条记录r 到类cluster 质心的距离d1与它到其它剩余记录的最近距离d2满足关系［11］：d1＜γ＊d2，且cluster的大小在 ［k，2k－1）内，则将r添加到类cluster 中；

End while

（5）若remaining＞0且类cluster的大小在 ［k，2k－1）之内，加入剩余记录后不会破坏类的k－匿名效果，则将剩余记录加入到距离最近的类；

（6）按照随机策略对生成的所有类实施交换操作，实现匿名化；

（7）将不能加入到任何类的记录隐匿；

（8）将匿名数据集发布；

End

W－V－MDAV 算法在选取聚类种子时充分考虑了距离以及权重值这2 个因素的影响，使得聚类种子的选取更优，聚类结果更加符合用户的期望度。然而该算法也还存在着聚类算法本身存在的比较耗时的问题，尤其是对大数据集进行聚类时，该问题较为突出。

为此，本文在W－V－MDAV 算法的基础上，进一步提出融合k－means和W－V－MDAV 算法的概率k－匿名方法，以实现对大数据集快速聚类，其主要思想是：给定原始数据集D 及其权重值集W 和匿名参数k，首先使用k－means算法快速地对D 进行初次聚类，得到k 个类；然后建立k个线程，分别对这k 个类并行地使用W－V－MDAV 算法进行再次聚类并对剩余记录进行处理；最后实施交换操作实现匿名化。

为了与k－匿名中的参数k 区分开，下面将k－means算法表述成c－means算法。

算法2：融合c－means与W－V－MDAV 算法的概率k－匿名算法

输入：原始数据集D，权重值集W，匿名参数k；

输出：匿名数据集T

Begin

（1）计算参数c：c＝f（n），n 为原始数据集D 的记录数，函数f（n）可由用户定义，如：f（n）＝n／1000×0.6［12］；

（2）使用c－means算法对D 进行初步聚类，得到c个类：C1，C2，...，Cc；

（3）for i＝1to c do in parallel

使用W－V－MDAV 算法对类Ci进行再次聚类并匿名化处理，得到局部聚类结果；

（4）若剩余记录数大于0，且有类的大小在 ［k，2k－1）之内，加入剩余记录后不会破坏类的k－匿名效果，则将剩余记录加入到距离最近的类中；

（5）按照随机策略对生成的所有类实施交换操作，实现匿名化；

（6）将不能加入到任何类的记录隐匿；

（7）将匿名数据集发布；

End

算法2将聚类算法c－means和W－V－MDAV 算法有效结合在一起，既实现了聚类和对敏感数据匿名化处理，又解决了算法在处理大数据集时耗时的问题。

2 实验结果与分析

实验硬件环境为AMD Athlon II X4 645 3.09 GHz CPU、4.0GB RAM，操作系统是Microsoft Windows XP，开发环境是Microsoft Visual Studio 2008，采用C＋＋语言以及多线程并行技术编程实现算法。本文采用的数据集是EIA 和Forest CoverType，采用与文献 ［13］一样的方法对Forest CoverType进行预处理，从其54个属性中选取10个有意义的数值型属性；并分别随机选取了10000、50000和100000条记录作为3个子数据集。

我们使用算法1表示本文给出的基于改进变长聚类的概率k－匿名算法W－V－MDAV，算法2表示本文给出的融合c－means与W－V－MDAV 算法的概率k－匿名算法。下列实验结果图中的数据集1、数据集2、数据集3和数据集4分别表示数据集EIA （4092条记录）、数据集Forest CoverType（10010条记录）、数据集Forest CoverType（50010条记录）和数据集Forest CoverType（100010条记录）。

图1和图2的实验结果给出了参数k 变化时，本文算法1 和文献 ［9］算法经过聚类之后匿名数据集的数据质量。

图1 相关系数之间差值的绝对值的平均值

图2 相关系数之间差值的绝对值的平均值

从图1和图2中可以看出，一方面，对于不同规模的数据集，本文算法1、文献 ［9］算法的平均值均随着k 值的增大呈缓慢增长趋势，这是因为随着参数k 值的增大，由于每个类的大小变大，原来在k 较小时不在同一个类的记录可能被聚类到一个类中，这必然会相对降低类内记录的相似性，使差异变大，相关系数之间差值的绝对值变大，平均值也相应增大；另一方面，当k 较小时，本文算法1的匿名数据集的数据质量略低于文献 ［9］算法；当k较大时，本文算法1 的匿名数据集的数据质量略优于文献［9］算法。

图3和图4的实验结果给出了聚类后本文算法1和文献 ［9］算法产生的信息损失度，对于不同规模的数据集，随着k值的增大，算法1、文献 ［9］算法产生的信息损失总体上均逐渐地增大，当k值较小时，文献 ［9］算法的信息损失度要略小于本文算法1；而当k 值增大到一定值时，算法1产生的信息损失几乎与文献 ［9］算法一样，有些还比文献 ［9］算法低一些。

使用聚类算法对数据集进行聚类之后，会剩下一些无法加入到任何类的记录，也就是剩余记录。剩余记录的选择因子的平均值大小反映了聚类时对聚类种子记录选择的好坏程度。剩余记录选择因子的平均值越大，说明剩余记录中本应该优先被选择做聚类种子进行聚类的记录没有被选中，本应优先被选中发布的记录没有得到发布，从而在一定程度上降低了匿名数据集的数据质量和数据可用性。

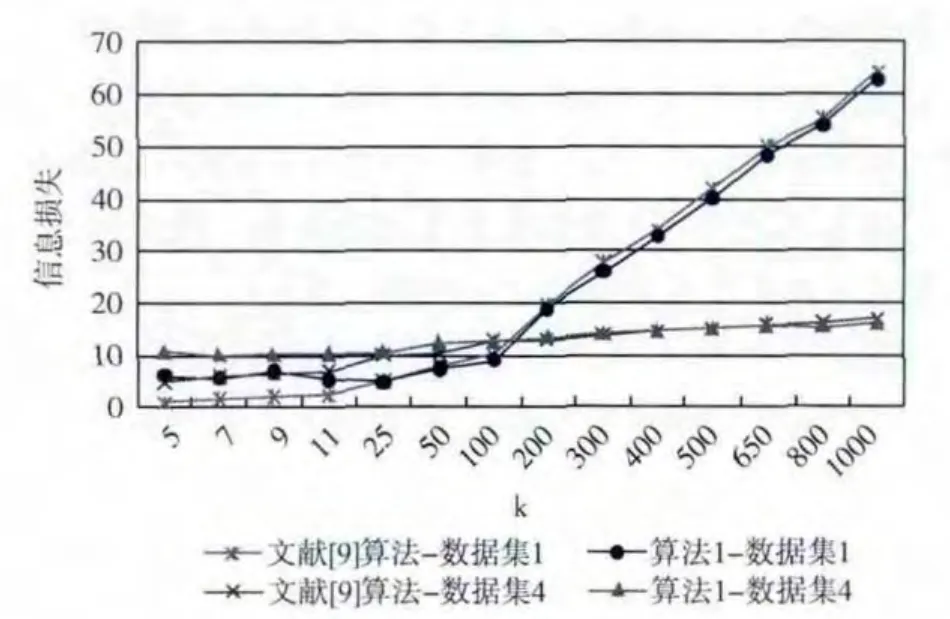
图3 信息损失度

图4 信息损失度

图5和图6的实验结果描述了本文算法1和文献 ［9］算法聚类后剩余记录的选择因子的平均值大小。

图5的实验结果表明，当k 值较小时，本文算法1 的剩余记录选择因子的平均值略大于文献 ［9］算法；而当k值增大到一定值时，本文算法1的剩余记录选择因子的平均值均明显地小于文献 ［9］算法。

图6 剩余记录选择因子的平均值

图6的实验结果表明，当k＝5时由于数据集大小刚好被k整除，文献 ［9］算法聚类之后没有剩余记录，所以剩余记录选择因子的平均值为0；对于其它k值，本文算法1的剩余记录选择因子的平均值总体上均明显地小于文献［9］算法。这是因为文献 ［9］算法在选择记录做聚类种子的时候只考虑了距离这个因素，它选择的是距离数据集质心最远的记录作为种子记录进行聚类，最后的剩余记录中很可能存在本应优先被发布的记录但没有被选取。本文算法1不仅考虑到记录距离质心的距离，还考虑了记录本身的权重值，根据这2个因素综合去选择更优的种子记录进行聚类。

综合图1～图6的实验结果分析可知，与文献 ［9］算法相比，本文算法1没有使信息损失度明显上升，也没有明显降低聚类前后数据集内各自相关系数之间差值的绝对值的平均值，从而没有降低匿名数据集的数据质量。本文算法1的剩余记录选择因子的平均值总体上均明显地小于文献 ［9］算法的平均值；聚类之后，本文算法1发布的匿名数据集的数据可用性高于文献 ［9］算法。

图7给出了对于不同规模的数据集，参数k 变化时，本文算法1和算法2在信息损失度方面的对比。

图7 信息损失度

图7的实验结果表明，对于不同规模的数据集、不同的k 值，本文算法2产生的信息损失度与本文算法1相比没有明显地增大，当k值较大时，2个算法产生的信息损失度几乎一样。

图8给出了对于不同规模的数据集，参数k变化时，本文算法1和算法2聚类后剩余记录选择因子的平均值的对比。

图8 剩余记录选择因子的平均值

从图8的实验结果中我们可以看到，对于不同规模的数据集和不同的k 值，本文算法2的剩余记录选择因子的平均值与本文算法1相差不大，聚类之后，算法2发布的匿名数据集的数据质量、数据可用性均与算法1基本相同。

对于不同规模的数据集和不同的k 值，表1给出了本文算法1与算法2所需的运行时间。

从表1 可知，对于不同规模的数据集、不同的k 值，算法2的运行时间均比算法1要少很多，且当数据集的记录数越多，算法2的优势越明显。这是因为c－means算法本身能快速地对大规模数据进行初步的聚类，而对经过cmeans算法处理后得到的c个类进行二次聚类、匿名化处理时，由于各个类之间并没有明显的关联，所以可以并行地进行聚类，从而可以显著加速算法的执行，大大减少算法所需的时间开销。

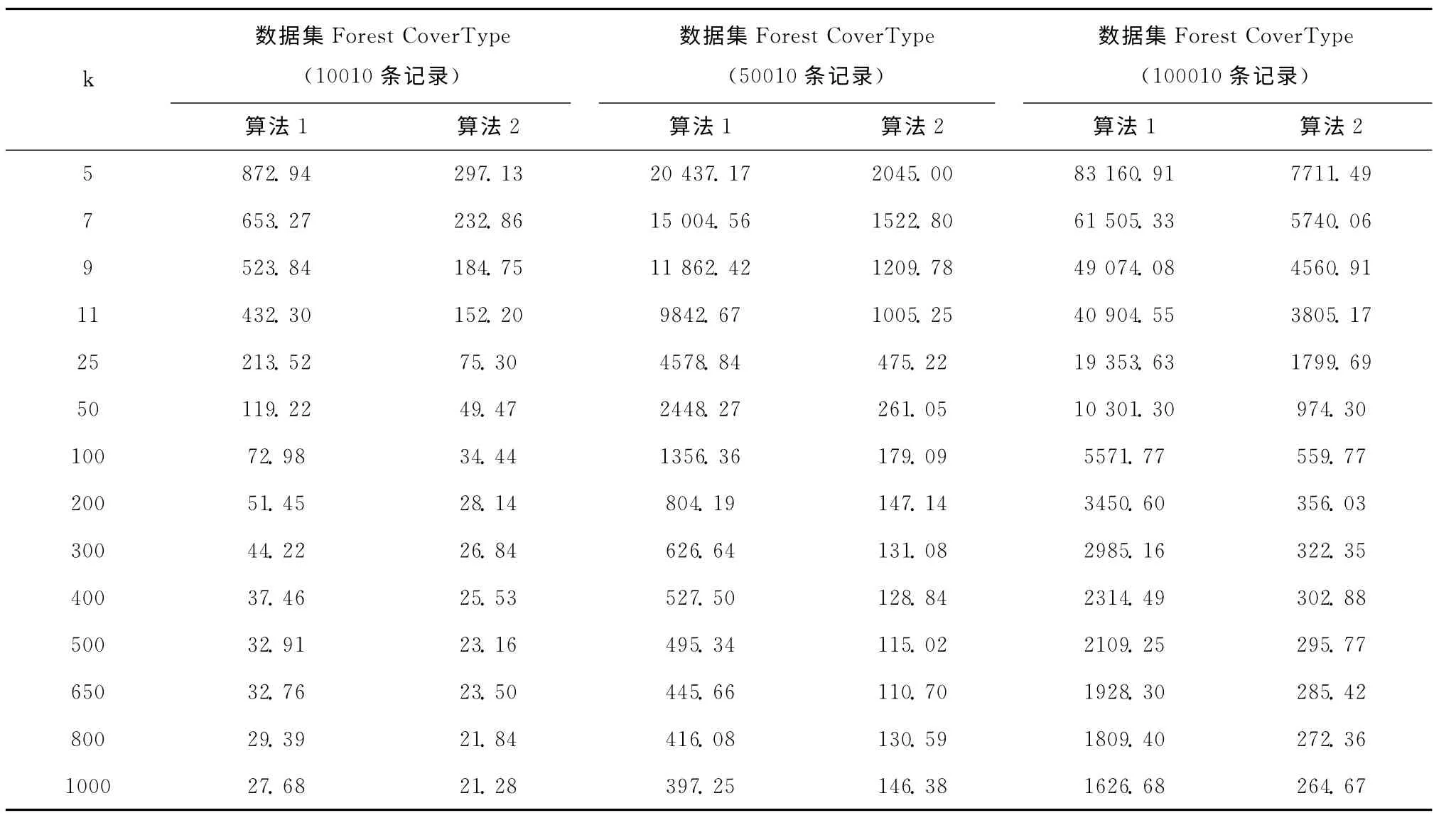
表1 本文算法1与算法2的运行时间对比／s

综上所述，与文献 ［9］算法相比，在获得相同的隐私保护程度的基础上，本文给出的算法1提高了匿名数据集的可用性；与本文算法1相比，在获得相同的隐私保护程度和匿名数据集可用性的基础上，本文给出的算法2很大程度地减少了运行时间，更适用于处理大数据集的基于聚类的多敏感属性数据匿名化。

3 结束语

本文综合考虑了记录之间的距离与记录本身权重值对聚类种子记录选取的影响，建立了聚类种子选择因子模型，提出了基于改进变长聚类的概率k－匿名算法，在选择聚类种子时考虑了用户对记录得到发布的期望值，从而使得发布的匿名数据集具有更高的数据可用性；同时，针对聚类算法在处理大规模数据时耗时长的问题，采用多线程技术并行聚类，使得融合k－means与W－V－MDAV 算法的概率k－匿名算法在不降低数据质量、不增加信息损失度的前提下，大大减少了处理大数据集所需的时间开销。下一步工作将研究基于混合型数据的聚类算法以及多敏感属性l－多样性匿名化算法。

［1］Wang Qian，Xu Zhiwei，Qu Shengzhi.An enhanced k－ano－nymity model against homogeneity attack ［J］.Journal of Software，2011，6 （10）：1945－1952.

［2］Sun Xiaoxun，Sun Lili，Wang Hua.Extended k－anonymity models against sensitive attribute disclosure ［J］.Computer Communications，2011，34 （4）：526－535.

［3］Sun Xiaoxun.A family of enhanced（L，α）－diversity models for privacy preserving data publishing ［J］.Future Generation Computer Systems，2011，27 （3）：348－356.

［4］TENG Jinfang，ZHONG Cheng.Clustering－based sensitive attribute l－diversity anonymization algorithms ［J］.Computer Engineering and Design，2010，31 （20）：4378－4381 （in Chinese）.［滕金芳，钟诚.基于聚类的敏感属性l－多样性匿名化算法 ［J］.计算机工程与设计，2010，31 （20）：4378－4381.］

［5］HAN Jianmin，CEN Tingting，YU Huiqun.Research in Microaggregation Algorithms for k－anonymity ［J］.Acta Electronica Sinica，2008，36 （10）：2021－2029 （in Chinese）.［韩建民，岑婷婷，虞慧群.数据表k－匿名化的微聚集算法研究［J］.电子学报，2008，36 （10）：2021－2029.］

［6］YANG Gaoming，YANG Jing，ZHANG Jianpei.Research on data publishing of privacy preserving ［J］.Computer Science，2011，38 （9）：11－17 （in Chinese）. ［杨高明，杨静，张健沛.隐私保护的数据发布研究 ［J］.计算机科学，2011，38（9）：11－17.］

［7］Md Enamul Kabir，Wang Hua.Systematic clustering－based microaggregation for statistical disclosure control［C］／／Proc of 4th International Conference on Network and System Security，2010：435－441.

［8］Panagiotakis Costas，Tziritas Georgios.Successive group selection for microaggregation ［J］.IEEE Transactions on Knowledge and Data Engineering，2013，25 （5）：1191－1195.

［9］Soria－Comas J，Domingo－Ferrer J.Probabilistic k－anonymity through microaggregation and data swapping ［C］／／Proc of IEEE International Conference on Fuzzy Systems，2012：1－8.

［10］Chettri S K，Borah B.An efficient microaggregation method for protecting mixed data ［C］／／Proc of the Fourth International Conference on Networks ＆ Communications，2013：551－561.

［11］Han Jianmin，Cen Tingting，Yu Huiqun.An improved V－MDAV algorithm for l－Diversity ［C］／／Proc of International Symposiums on Information Processing，2008：733－739.

［12］Han Jianmin，Yu Juan，Yu Huiqun，et al.An efficient kanonymization algorithm combining C－modes with MDAV［C］／／Proc of IEEE International Confe－rence on Granular Computing，2008：257－260.

［13］Marc Solé，Victor Muntés－Mulero，Jordi Nin.Efficient microaggregation techniques for large numerical data volumes［J］.International Journal of Information Security，2012，11（4）：253－267.