高中数学回归基础与返璞归真

张小琴

从事高中数学教育教学10多年来，笔者在不断思索、总结，高中数学知识中深奥的理论如何讲解。笔者发现，最容易让学生理解的教学方式，就是让学生亲身经历，亲自动手参与，或师生共同演示教具。让学生直观的去感受，亲身经历知识发生的过程，再由此升华为数学中的系统的理论知识，从而突破教学中的重点和难点，提高教学效率。同时，动手操作，也使得学生学习数学理论的积极性得以提高，增加学习的热情。下面举一些教学实践中成功的例子。

制作教具的作用

学习正弦函数的图像时，首先根据正弦函数的解析式，

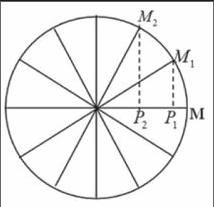
列表将单位圆十二等分，以为横坐标，再以这些角对应的正弦值为纵坐标列表，而实际上以正弦线来表示改角的正弦值更为精确。但事实上是，如何将自变量弧度和它对应的正弦值M1P1表示在横坐标和纵坐标上？最精确的做法就是做一个单位圆模型，用厚一点的纸箱皮做，在单位圆的外侧粘双面胶，同时用一些有铝丝的塑料彩纸条（容易固定）固定在如图所示的M1P1，M2P2等的位置，下面以（0，0）为起始点开始转单位圆的圆盘，此时点M与坐标系的坐标原点重合，当圆盘上的双面胶粘在x轴上，到M1的位置时，此时，彩纸条M1P1正好垂直于x轴，此时确立第一个点P1点，其横坐标为圆弧MM1的长，纵坐标为彩纸条M1P1的长，这样做，保留了在确立角和对应的正弦值的最真实（相对）的数据。依次确立其他各点，注意，在确立其他各点的过程中，当角大于π时，将双面胶上的塑料彩纸条粘在单位圆的外侧边上，并放在圆盘背面，这样展开的时候这些彩纸条会落在坐标系中x轴的下方。展开之后，依次描点连线，则正弦函数在一个周期内的图像就呈现出来了。

引导学生继续思考，如果角大于2π或角小于0，此时的图像是什么情况，学生自然想到只需继续转动圆盘，图像就呈现出来，紧接着，就可总结出正弦函数图像的周期性，通过圆盘演示，学生观察到了正弦函数最大的特征——周期性。

笔者在教学过程中，使用该教具教学，形象直观，易于理解。对比其他的画图法，如独立的确定横纵坐标：先将横坐标0：2π分12等分，确立横坐标，然后在单位圆中平行移动M1P1与对应，M1P1即为横坐标为时对应的纵坐标，依次再确立其他各个点。这种方法不管是老师在黑板上手工操作还是用电脑几何画板演示，笔者认为都没有用教具来的直观、清晰、明了。

在学习圆锥曲线时，椭圆和双曲线轨迹的形成过程中，使用教具讲解，形象直观。在一根绳子的两端分别系一个吸顶器（小），操作中，将两个吸顶器分别固定在黑板上，然后用粉笔将绳子拉直在黑板上画线，观察曲线的形状（交给学生操作）。再调整两吸顶器之间的距离再画曲线，观察两吸顶器之间的距离和所画出的椭圆的形状之间的关系。并将两吸顶器之间的距离达到最大观察此时能不能画出图像，再将两吸顶器重合，观察画出来的图像。操作完之后，动点的轨迹（粉笔运行的轨迹）即椭圆的定义清晰明了，同学们就能快速总结出来。且通过实践操作什么时候形成椭圆、圆、线段，图像不存在，也能直观的看到。课下还可以把教具留给课堂没有机会画的同学体会。同样，在学习双曲线的定义时，也是使用类似的教具，教学效果好，学生理解透彻。当然这需要教具做到位，演示具体清晰。反之，若教具做的不精致，操作不到位，草草演示完了，学生仍然云里雾里，不知所云，更不要谈学习的效率了。所以，教学效果要好，教具制作一定要到位。

自己动手做教具

在学习立体几何时，很多同学因为缺乏空间想象能力而无法将该部分内容学好，“缺乏空间想象”这是天生的，无法改变，但学生们可以通过后天的努力积极改变——制作立体几何教具，观察教具，复杂的点、线、面的关系一目了然，抽象的想象变得清晰可见。在一开始接触立体几何，讲空间几何体时，便要求学生自己制作教具，如柱体、椎体等;在学生制作的过程中，这些几何体的模型深深映在学生的脑海中;在以后的学习中遇到该几何体时，这些模型很快就浮现在脑海中，帮助学生解题。除了学生自己制作教具，学生还需要随时观察生活中的几何模型。

知识点的迁移

教具的制作属于教学模型的范畴，知识点的迁移同样也属于教学模型的范畴，只不过前者是实物与理论结合，后者是学习过的理论与未学习的理论的连接。比如，在学习平面向量的加法时，向量加法的两个加法法则不用老师按部就班地去讲;事实上，在物理上讲两个力的合成和求两个位移的和中，学生早就已经熟练了。因此，向量加法法则并不是一堂新课，只要回忆清楚力的合成的原则和求两位移的和的原则，再指出物理中的矢量就是数学中的向量，那么，在平面中任意给两个向量，求作两向量的和，学生顺理成章就做出来了，法则也随之总结出来。

（作者单位：内蒙古自治区阿拉善盟第一中学）endprint