薄膜温度计安装接触热阻和激励功率的优化

张 祥 周 刚 李 青

(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190)

(2国家核电技术研发中心 北京 100190)

1 引言

薄膜电阻式温度计在正常使用的过程中，当通过工作电流时会产生焦耳热(温度计自热)。温度计的自热效应必须限制在一定的范围内，才能使温度计和被测物体之间的温差不超过实验精度所给出的限制。温度计的自热效应与温度计安装的接触热阻有着密切的关系［1-2］。低温温度计一般安装在高真空或液氦环境下的铜块上。在这种条件下，热阻主要取决于温度计工作温区、热环境和温度计安装的方式［3-5］。

通常情况下，温度计安装的接触热阻很难精确测量与计算，并且随着温度计的重新安装、温度变化引起的热物性参数变化以及周围热环境的变化而变化。在温度计实际安装过程中许多未知的细节问题(例如安装过程中使用的清漆或者环氧脂等材料的厚度无法精确测量)严重影响接触热阻的测量与计算。此外，材料在低温下的热物性参数也是随着温度变化而变化的，而且无法精确的获得。当温度低于4 K以下时，卡皮查热阻的影响不能忽略，并且难于计算。

温度计自热效应的处理主要有以下两种方法:(1)增加温度计的输出功率使其温度升高，然后计算得到温度计零功率输出时的温度值，但是这种方法并不适用于半导体二极管类的非线性温度计;(2)在工作温区直接测量接触热阻并且计算温度计的理想工作条件［6］。通过测量温度计安装接触热阻可以评估温度计的最优激励条件、自热效应以及测量系统本身的性能指标。在本文中采用双电流法计算温度计安装的接触热阻值［7-8］。

2 理论模型

2.1 双电流法计算温度计安装接触热阻

温度计在使用过程中的耗散功率可以表示为:

式中:I为通过温度计的激励电流，A;R为温度计自身的电阻值，Ω。自热效应使得温度计与被测点或区域之间存在温度梯度，正是这种温度梯度导致了温度计实测值高于被测点或区域的真实值。由温度计自热效应引入的温度梯度也可以表示为:

式中:Rt为温度计安装的接触热阻，K/W。Rt通常由两部分组成:

式中:Rti为由温度计自身结构引起的内热阻值，是温度计的本征属性;而Rte为温度计与安装表面之间的接触热阻值，也是本研究讨论的重点。温度计安装接触热阻Rt的大小主要取决于温度计工作温区、安装表面的粗糙度、热环境以及温度计安装的方式等因素。

温度计的自热效应也可以表示为电阻的形式:

双电流法是一种简单而又有效的计算温度计安装接触热阻的方法。由式(4)可知，利用不同的激励电流I可以测得不同的温度计电阻值R，并且可以通过温度计的分度表转化为温度计的自热效应ΔT，进而求出温度计安装接触热阻Rt。这就是双电流法计算温度计安装接触热阻的基本原理。通常情况下，为了简化计算和便于实验的操作，假定激励电流I1下测得的温度计电阻值为R1，R2为激励电流时测得的温度计电阻值，引入零功率电阻R0的概念。R0与R1和R2的关系可以表示为:

式中，s为温度计的灵敏度系数。

同理，ΔT也可以表示为双电流的形式:

式中，X0和X1分别表示电流为I0和I1时所测得的电阻比。此外，

将式(8)代入(7)中，可以得到:

因此，温度计安装接触热阻Rt可以表示为:

值得注意的是，由双电流法推导得到的温度计安装接触热阻的理论关系式(10)是在温度计的耗散功率与温升呈线性变化关系的背景下计算得到的。但是对于锗电阻或者碳玻璃纤维等电阻式温度计，尽管其自身的耗散功率与温升呈非线性变化的关系，式(10)仍然适用。

2.2 热阻测量的不确定度分析

测量不确定度定义为表征合理地赋予被测量之值的分散性，与测量结果相联系的参数。此参数可以是标准差或其倍数，或说明置信水准的区间的半宽度，其值恒为正值。对于高精度的低温温度测量而言，引起温度测量的不确定度主要包括:电阻测量引起的不确定度、测量仪器的精度和分辨率、温度计分度表转化引起的不确定度、温度计自热效应、热电效应和零点偏移、热噪声、电磁干扰以及系统漏热等因素。本文仅讨论温度计安装接触热阻的测量不确定。

由前述分析可知，采用双电流法能够有效计算温度计安装的接触热阻。在接触热阻的不确定分析过程中，需要引入对激励电流I1和I2的修正，并将此修正传递到零功率下的电阻测量中。因此，就式(8)而言，X=X(I1)X(0)被定义为激励电流I1下的自热修正项。对式(8)微分，可得误差传递方程:

式(11)由两部分组成:前两项表示电桥测得的电阻比的不确定度，后一项表示激励电流的不确定度。此外，进一步分析式(11)可知:由激励电流引起的不确定度和温度计自热效应成正比的关系(中括号内的部分);当激励电流的相对误差相同时，即，零功率测得的电阻比的不确定度仅与电桥测得的电阻比的不确定度有关。因此，自热修正的相对不确定度可以表示为:

当激励电流的关系为I2=时，激励电流1%的不确定度会引起温度计自热修正5.6%的不确定度。通常情况下，激励电流的不确定度在0.1%和1%之间变化，因此由激励电流不确定度变化造成的温度计自热修正的不确定度最大值低于5.6%。对于精度要求不高的测量环境，激励电流I2=的关系通常能够满足自热修正的精度范围。然而在高精度的低温温度测量系统中，需要通过多电流的方式计算得到温度计自热效应修正的最优激励电流关系。

同样对式(10)微分，得到接触热阻计算的误差传递方程:

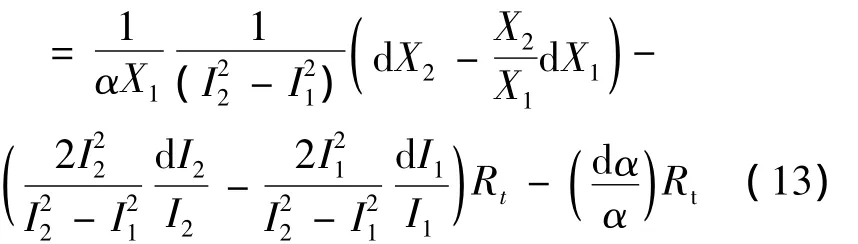
因此，温度计安装接触热阻的不确定度可以表示为:

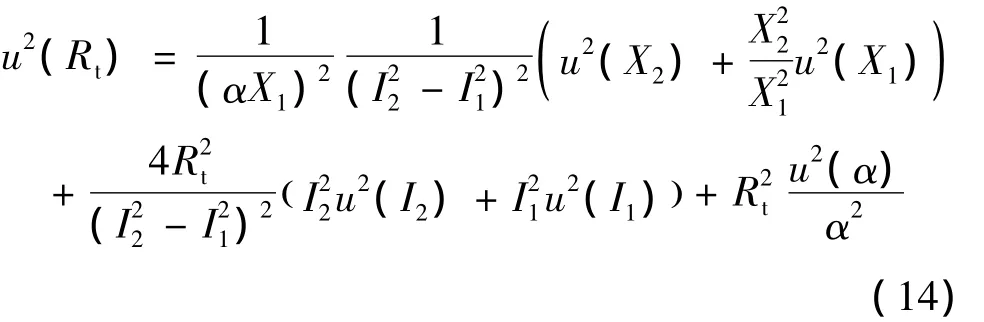
上式中，u(X)和u(I)分别表示电桥测量的电阻比和激励电流的不确定度，而u(α)表示温度计灵敏度系数拟合的不确定度。

2.3 温度计最优激励条件的选择

低温温度计与被测区域之间任何一点微小的扰动都会引起温度测量的误差或不确定度。温度计自身的耗散功率会导致其温度的升高以至于高于被测环境实际的温度。对于电阻式温度计，温度计的自热效应不可避免。温度测量不确定度的最小化要求由温度计自热效应和测量仪器输出信号引起的不确定度的平衡。此外，还需要考虑温度计的安装方式、被测区域的热环境以及电磁噪声等诸多不确定因素对温度测量的影响［9-10］。因此，合成不确定度uc定义为各个相互独立的测量不确定度分量ui的合成:

值得注意的是在使用式(15)进行合成不确定度的计算之前，需要统一各个相互独立的不确定度分量的单位。例如在本文低温温度测量的不确定度评定时，需要首先将温度计测得的电阻不确定度转化为温度不确定度，再进行合成不确定度的计算。

对于输出电压信号的温度计而言，温度测量不确定度uT和电压测量不确定度uV的关系可以表示为:

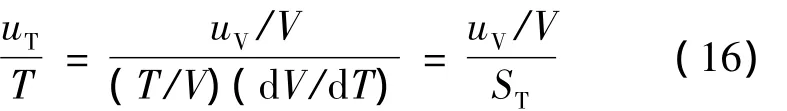
式中，ST=(T/R)(d R/d T)定义为无量纲的灵敏度系数，R为温度T下的温度计电阻值。此外，无量纲的灵敏度系数也可以表示为d(ln R)/d(ln T)对数的形式。对于其它输出信号为电流、电容或者压力的温度计，只需将式(16)中的电阻R转化为相应的电流I、电容C或者压力P等参数即可。

由式(16)可知，在电压测量不确定度不变的条件下，增大温度计的输出电压可以降低温度测量的不确定度，然而随着温度计激励电压的增加势必会导致温度计自热效应的增加。因此，在温度计自热效应与温度测量不确定度最小化的前提下，必然存在温度计最优的激励条件，同时满足上述两者的要求。在实际测温过程中，有时常以加大工作电流或电压来增加温度计的灵敏度，此时也需要计算温度计的最优激励条件以平衡温度计自热和灵敏度之间的关系。

温度计最优激励条件的选取主要考虑温度测量不确定度的最小化和温度计自热效应的平衡关系。具体求解过程如下:

(1)联立式(16)和(2);

(2)将计算结果代入式(15)的右边项中，并求解得到式(17)，注意式(17)仅包含温度计自热和测量仪器的输出条件两项;

(3)对式(17)中的温度计输出功率P求微分;(4)令微分方程为零;

(5)求解得到温度计的最优激励条件。

温度计的最优激励条件可以表示为:

式中，将其它引起测量不确定度的因素等效成电压的形式，因此电压测量的不确定度以级数的形式表示。此外，由式(18)可知，温度计的最优激励条件与温度计安装的接触热阻呈反比例的关系。因此，降低温度计安装的接触热阻能够有效的提高温度计的最优激励条件，并提高温度计使用过程中的灵敏度。

3 实验结果与分析

研究作为实验测量用的低温温度计为Cernox-1050-SD(SN X70208)，采用VGE-7031清漆将其安装在高导无氧铜样品架上。测量仪器选用美国Fluke公司出品的1594A超级数字温度计，其一年期精确度为0.8×10－6(0.2 mK)。图 1 所示为在实验温区4.2¯20 K范围内，温度计激励电流与自热效应和标准偏差的关系。如图所示，随着温度计激励电流的增加，温度计的自热效应明显增强，然而温度测量的标准偏差却逐渐降低。因此，在实验条件和测量仪器不变的条件下，必然存在着温度计的最优激励电流，使得温度测量的不确定度达到最小，这也从实验的角度验证了上述的理论分析。

图1 温度计激励电流与自热效应和标准偏差的关系Fig.1 Variation among excitation current，temperature and standard deviation at different temperatures

温度计最优激励条件的计算结果列于表1中。作为典型的负温度系数温度计，Cernox温度计的电阻和无量纲的灵敏度系数随着温度的升高而降低，因此温度计的最优激励电流随着温度的升高而逐渐升高。在4.2¯20 K温区范围内，温度计的最优激励电压均大于温度计使用手册中的推荐值2 mV±25%。因此，对于高精度的低温温度测量，在温度计的实际使用过程中，必须首先根据实际的安装环境测得温度计安装接触热阻值，进而求得温度计的最优激励条件，并以此激励条件激励温度计，这样才能满足高精度的温度测量需求。

表1 温度计最优激励条件的计算结果Table 1 Optimal sensor excitation power at different temperatures

表2所示为温度计安装接触热阻的不确定度计算结果以及由热阻测量不确定度引起的温度计自热不确定度。值得注意的是表2的温度计激励电流是由表1计算得到的。温度计自热效应引起的温度测量不确定度是由Popt×Rt计算得到的，并且在20 K时达到最大值0.896 mK，在4.2 K时为最小值0.377 mK，均低于1 mK。

表2 热阻测量的不确定度计算结果Table 2 Uncertainties due to measured effective thermal resistance

4 结论

首先从温度计自热效应的角度出发，采用双电流法理论分析了温度计安装的接触热阻，详细推导了接触热阻的不确定度计算公式;其次从温度测量不确定度的最小化要求由温度计自热效应和测量仪器引入的不确定度平衡的角度出发，理论推导得到了温度计最优的激励条件计算公式，并由温度计激励电流与自热效应和标准偏差的实验关系验证了温度计在实际使用过程中必然存在着最优的激励条件。实验结果表明:在不同的实验温区4.2¯20 K范围内，温度计的最优激励电压均大于温度计使用手册中的推荐值2mV±25%;温度计自热效应引起的测量不确定度在20 K时达到最大值0.896 mK，在4.2 K时为最小值0.377 mK。

因此，对于高精度的低温温度测量，在温度计的实际使用过程中，必须首先根据实际的安装环境测得温度计安装的接触热阻值，进而求得温度计的最优激励条件，并以此激励条件激励温度计，这样才能满足高精度的温度测量需求。

1 Courts SS，Davenport WE.Thermal resistances of cryogenic temperature sensors from 1-300K［J］.Adv.Cryogenics Engineer，2000(45):1-10.

2 Yeager C J，Courts SS.Thermal resistance of cryogenic thermometers at ultra-low temperatures［J］.Adv.Cryogenics Engineer，2001，613:1644-1650.

3 Sparks L L.Temperature，strain，and magnetic field measurements［J］.Materials at Low Temperatures，1983:515-521.

4 Kobel T A，Kozyrczak M A.Effects of mounting methods on temperature sensor accuracy below 10 K［J］.Supercollider，1992(4):619-626.

5 Kreitman M M，Callahan J T.Thermal conductivity of Apiezon N grease at liquid helium temperatures［J］.Cryogenics，1971(10):155-159.

6 Holmes D S，Courts S S.Thermal resistances of mounted cryogenic temperature sensors［J］.Adv.Cryogenics Engineer，2001，41B:1699-1706.

7 Batagelj V，Bojkovski J.Influence of SPRT self-heating on measurement uncertainty in fixed point calibration and calibration by comparison［J］.Temperature:Its Measurement and Control in Science and Industry，2002(7):315-320.

8 Batagelj V，Bojkovski J.Methods of reducing the uncertainty of the self-heating correction of a standard platinum resistance thermometer in temperature measurement of the highest accuracy［J］.Measurement Science ＆ Technology，2003，14:2151-2158.

9 Temperature measurement resolution and uncertainty in Temperature Measurement and Control catalog［J］.LakeShore Cryotronics ，1999:A-47.

10 Neil T，Van Dresar.An uncertainty analysis of the PVTgauging method applied to sub-critical cryogenic propellant tanks［J］.Cryogenics，2004，44:515-523.