U型脉冲管制冷机中冷头连接管的影响

张祥镇 胡剑英 崔 浩 张丽敏 罗二仓

(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190)

(2中国科学院大学 北京 100049)

(3航天低温推进剂技术国家重点实验室 北京 100190)

1 引言

斯特林脉冲管制冷机是一种利用声功来获得制冷效应的低温制冷机，制冷的基本原理是热声效应。其突出的优点是在低温下没有任何的运动部件，结构设计简单，同时采用线性压缩机驱动，消除了机械磨损，因而与传统的制冷机械相比，具有更高的可靠性和更长的寿命。

虽然目前的低功率脉管制冷机的结构尺寸较小，整体占用空间不是很大，但是其常见直线式的布局造成了脉冲管制冷机系统的窄长的结构特点，这不利于系统的紧凑性，也不便于冷量的提取。为了克服该缺点，把脉冲管制冷机的脉管与回热器平行布置，就构成了U型脉冲管制冷机。与直线脉管制冷机相比，其在回热器冷头和脉管之间多了一根连接管，可能对制冷机的性能产生一定的影响。U型脉管的研究虽然很多，但是到目前为止，关于回热器冷头与脉管之间的连接管对制冷性能的定量研究却极为少见。基于此，依据经典的线性热声理论，研究将对连接管的影响进行系统的数值模拟。

2 有连接管的脉冲管制冷机系统

U型脉冲管制冷机系统的结构如图1所示，包括主水冷器、回热器、冷端换热器、冷头连接管、脉冲管以及调相结构，并在冷头连接管与脉管之间设置导流结构，表1给出了此制冷机的主要结构参数。整个制冷机由直线压缩机驱动，采用氦气作为工质，通过惯性管和气库来调相。该制冷机与以往直线脉管制冷机最大的不同是在冷端换热器与脉冲管之间有一段连接管。

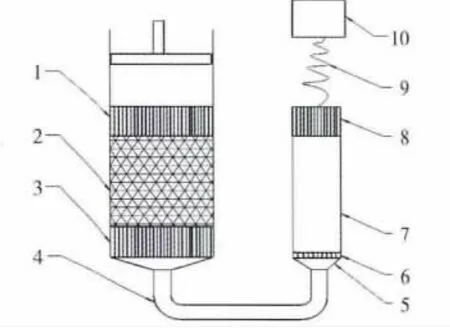
图1 实验装置示意图Fig.1 Schematic diagram of experimental apparatus

表1 U型脉冲管制冷机的主要结构参数Table 1 Dimensions of the U-shape pulse tube refrigerator

在实验过程中，不可能对调相结构换来换去，同时也为了实验间的严格对比，因而要将其确定下来。确定调相结构的参数需要选定具体的制冷温度和压比，还要考虑连接管参数、导流情况以及连接管两端锥管长度的影响。这里是在充气压力2.5 MPa、频率60 Hz、冷头温度 77 K、压比 1.2、导流长度 3 mm、导流用80目紫铜丝网、连接管两端锥管长度均为6 mm、连接管直径5 mm和连接管长度70 mm的设定条件下优化后的结果。

连接管的直径变化对惯性管的最佳参数有着明显的影响，同时，惯性管的变化反过来对连接管最佳管径也有影响。实验可以通过不断的交替优化而得到最佳的惯性管参数和最佳的连接管径，然而这对研究目的帮助不大，以及此前计算的最佳直径多在5 mm左右，综合考虑后，这里设定连接管直径为5 mm。

图2表示冷头温度77 K、压比1.2、连接管长度70 mm、连接管直径5 mm、导流长度3 mm、导流丝网为80目紫铜丝网、连接管两端锥形管长度均为6 mm、惯性管直径4 mm的条件下相对卡诺效率和制冷量随惯性管长度的变化情况，根据相对卡诺效率最大值来求得最佳长度为1.800 m。

图2 相对卡诺效率及制冷量随惯性管长度的变化Fig.2 Relative Carnot efficiency and cooling capacity vs.length of inertance tube

图3表示其它条件不变的情况下，惯性管长度定为1.800 m后相对卡诺效率和制冷量随惯性管直径的变化情况，根据相对卡诺效率最大值来求得惯性管最佳直径为4.04 mm≈4 mm。

综上分析，选定惯性管的基本参数为直径4 mm、长度 1.800 m。

3 数值模拟的计算模型

图3 相对卡诺效率及制冷量随惯性管直径的变化Fig.3 Relative Carnot efficiency and cooling capacity vs.diameter of inertance tube

自从脉冲管制冷机问世以来，对脉管制冷机已经建立了许多理论，比如焓流相位理论、向量分析法等［1］，这里采用经典的线性热声理论［2］，其依据流体最基本的连续性方程、动量方程、能量方程以及气体物性方程，在小振幅振荡假设和简谐振动条件下引入复数符号，并进行线性化后得到基本的热声方程。最终得到的圆管、换热器、回热器中的控制方程如下［5］:

式中:P为压力，Pa;U为体积流;H为总能流;Q为换热量;Z1、Z3为单位长度流道的声导纳和声阻抗;Z2与单位长度流道的功产生有关，在不同的脉冲管制冷机部件中有不同的表达式，见参考文献［5］。这3个基本方程是对脉冲管制冷机进行模拟计算的基础，本系统的计算就是在以上基本方程的基础上完成的。

表2是下面研究的参考参数，在每一步探究过程中，我们只改变其中的一项来进行对比，具体的参数变化在下面相应的条目中指明。

表2 模拟过程中的不变参数Table 2 Constant parameters of simulation

4 连接管尺寸对制冷性能的影响

4.1 连接管长度对制冷性能的影响

图4表示把表2中连接管长度分别设为35、70和105 mm时相对卡诺效率随冷头连接管直径的变化曲线，图5表示相同条件下制冷量的变化情况，此两幅图旨在探究制冷机性能随连接管直径和长度的变化情况。

图4 不同连接管长度时相对卡诺效率随连接管直径的变化Fig.4 Relative Carnot efficiency vs.diameter of connecting tube for different length of connecting tube

从图中可以看出:(1)不论是从相对卡诺效率角度还是从制冷量的角度来看，连接管都存在一个最佳直径;(2)连接管长度的变化对连接管最佳管径(据效率)的影响非常小，35、70和105 mm对应的最佳直径分别是 4.41、4.56 和4.62 mm(此数据从模拟结果得到);(3)在最佳管径附近，连接管长度对相对卡诺效率的影响相对较小，而在其它管径处，不同连接管长度的相对卡诺效率相差则相对较大;(4)固定连接管管径下的制冷效率随着管长的增大而减小，这一点符合经验。

图5 不同连接管长度时制冷量随连接管直径的变化Fig.5 Cooling capacity vs.diameter of connecting tube for different length of connecting tube

4.2 压比对连接管最佳直径的影响

图6表示把表2中压比分别设为1.20、1.25、1.30时相对卡诺效率随着冷头连接管直径的变化曲线，旨在探究压比对最佳直径的影响。

从图中可以看出:(1)相对卡诺效率随压比的变化并没有明显的规律性，只是在压比1.25时的效率相对较高;(2)压比分别为 1.20、1.25、1.30 时最佳直径依次为 4.58、4.37、4.26 mm，即随着压比的增大，所需要的冷头连接管最佳直径将变小。

图6 不同压比时相对卡诺效率随连接管直径的变化Fig.6 Relative Carnot efficiency vs.diameter of connecting tube for different pressure ratio

4.3 连接管最佳直径随制冷温度的变化

图7表示把表2中的制冷温度分别设为60、77和100 K时相对卡诺效率随着冷头连接管直径的变化曲线，此图旨在探究制冷温度对最佳直径的影响。从图中可以看出:(1)随着制冷温度的提高，相对卡诺效率增加明显;(2)可以得到制冷温度分别为60、77和100 K 时对应的最佳直径依次为4.44、4.58 和4.70 mm，随着制冷温度的升高，所需最佳直径略微增大，制冷温度对冷头连接管最佳直径的影响不是很明显。

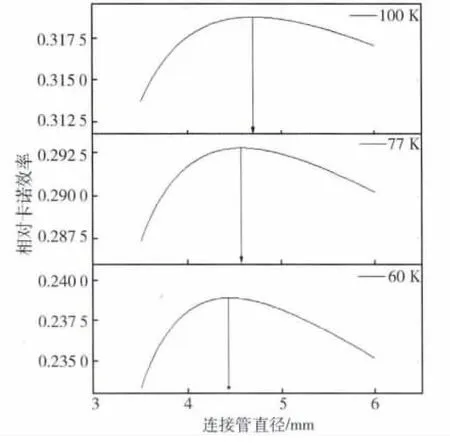
图7 不同制冷温度时相对卡诺效率随连接管直径的变化Fig.7 Relative Carnot efficiency vs.diameter of connecting tube for different refrigerating temperature

5 导流结构、锥管对制冷性能的影响

5.1 脉管导流的影响

图8表示在改变表2中脉管导流长度时制冷性能的变化曲线。制冷的相对卡诺效率随着导流长度近乎线性变化，导流段越长，制冷性能越差。这是因为丝网导流层越厚，阻力损失越大。

表3列出了改变表2中导流丝网目数时制冷性能的变化情况，在流动为层流时，丝网目数越大，制冷性能下降明显。这是因为丝网目数越大，水力直径越小，阻力损失较大的原因。因此在实际系统中，在导流层能够使流动充分均匀化的前提下，导流层应该采用尽量小的丝网目数。

表3 导流丝网目数Table 3 Mesh number of screens for flow straightener

5.2 连接管两端锥管长度的影响

图9表示改变表2中连接管两端锥形管长度时制冷性能的变化曲线。可以看出，层流时，锥管长度增大，制冷性能变差。

6 总结

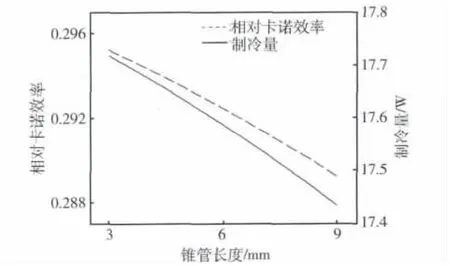
图9 相对卡诺效率及制冷量随锥形管长度的变化Fig.9 Relative Carnot efficiency and cooling capacity vs.cone length

本文通过数值计算研究了U型脉冲管制冷机冷头连接管对制冷机性能的影响。结果表明，对于固定的连接管长度，总是存在最佳的直径以获得最高的效率。连接管长度、压比和制冷温度对最佳直径有一定影响，但是不明显。另外，在最佳直径附近，连接管长度变化对制冷效率的影响较小，而在其它直径处，则影响较为明显。最后还对连接管脉管之间导流和连接管两端锥管进行了计算模拟，发现当导流长度和导流丝网目数越大时，制冷性能变得越差。由于经典的线性热声理论无法对弯管损失进行计算，对弯管交变流动的模拟和实验验证将是下一步的研究工作。

1 陈国邦，汤 珂.小型低温制冷机原理［M］.北京:科学出版社，2010:177-300.Chen G B，Tang K.The Principle of Small Cryocoolers［M］.Beijing:Science Press，2010:177-300.

2 Swift G W.Thermoacoustics:A unifying Perspective for Some Engines and Refrigerators［M］.New York:AIP Press，2002.

3 Ward B，Clark J，Swift G.Design Environment for Low-amplitude Thermoacoustic Energy Conversion，DeltaEC Version 6.3bll Users Guide［M］.DeltaEC.2008.

4 Hu J Y，Dai W，Luo E C.Development of High Efficiency Stirlingtype Pulse Tube Cryocoolers［J］.Cryogenics，2010，50:603-607.

5 胡剑英.液氮至液氢温区的热声驱动低温制冷机的研究［D］.北京:中国科学院理化技术研究所，2007.Hu Jianying.Study on Heat-Driven Thermoacoustic Cryocoolers Operating in The Cryogenic Temperature Range From Liquid Nitrogen to Liquid Hydrogen:［D］.Beijing:Technical Institute of Physics and Chemistry of CAS，2007.

6 Ferziger J H.Computational Methods for Fluent Dynamics［M］.New York:Springer-Verlag Berlin Heidelberg，2002.

7 罗二仓，戴巍，吴张华，等.交变流动热机的介观热力循环理论-第一部分:制冷机回热器的介观热力循环模型及分析［J］.低温工程，2004，137:1-11.Luo E C，Dai W，Wu Z H.Meso-scope Thermodynam ic Theory for Cyclic Flow Engines-Par tⅠ:The Cryogenic Regenerators［J］.Cryogenics，2004，137:1-11.

8 吴张华.电驱动室温温区行波热声制冷机的数值模拟及实验研究［D］.北京:中国科学院理化技术研究所，2006.Wu Zhanghua.Theoretical and Experimental Study of Electrically Driven Traveling-wave Thermoacoustic Refrigerator in Room Temperature Range［D］.Beijing:Technical Institute of Physics and Chemistry of CAS，2006.

9 王晓涛，胡剑英，戴巍，等.液氮温区高效脉冲管制冷机的特性研究［J］.工程热物理学报，2010，31(5):742-744.Wang X T，Hu J Y，Dai W.Study on a high efficiency pulse tube cooler operating in liquid nitrogen temperature ［J］.Journal of Engineering Thermodynamics，2010，31(5):742-744.