基于DSP技术的电力系统数据采集仿真测试的实现

李铁款

（广东电网公司佛山三水供电局，广东 佛山528100）

0 引言

基于DSP技术的电力远动系统数据采集是采用数字信号处理方法中的FFT（快速傅里叶变换算法），将数据采集的电流、电压中的干扰转化为高次谐波，避免模拟滤波电路参数不匹配带来误差，大大提高了测量精度。本人根据数字信号处理原理及应用DSP芯片、MPU芯片双CPU为核心的电力微机远动装置的设计思路，进行了相关软件算法设计的仿真测试，实现电参数的测量功能。

对一个已明确的频率、幅值、相位待测信号进行加窗傅里叶分析，通过Matlab和CCS得出仿真结果，算法可行性得到验证，为实现DSP系统的硬件电路的设计奠定基础。

1 测试信号波形图

通过Matlab程序对信号进行分析，设基波频率为50Hz；直流分量为10，基波幅值20，二次谐波幅值10，三次谐波幅值15，表达式如下：

测试信号波形图如图1所示，测试信号傅里叶变化图如图2所示。

图1 测试信号波形图

2 基波频率仿真分析

分析基波频率，通过一个简单的待测信号f（t）＝sin（ω0t＋φ1），可以得出φ1，要得出f（瞬时频率），或者ω0，就要在时间上平移原信号，得到平移后的信号：

f′（t）＝sin［ω0（t－Δt）＋φ1］＝sin［ω0t＋（φ1－ω0Δt）］ （2）

一个时间Δt的改变量对应于一个Δφ＝ω0Δt的相位改变量（图3）。

图2 测试信号傅里叶变化图

图3 解卷绕后相位随时间的变化

由于f＝2πω，Δt→0，可以得出：对θ求导即可确定被测信号中该频率分量的瞬时频率f。即：

做平移，则可得到平移m个Δt后h次谐波所对应的ah和bh的表达式：

求得平移后的相位，并得到幅值与平移时间的关系：

以上频率的数值多在50Hz左右波动，可以得出基频频率为f1＝50Hz（图4、图5）。

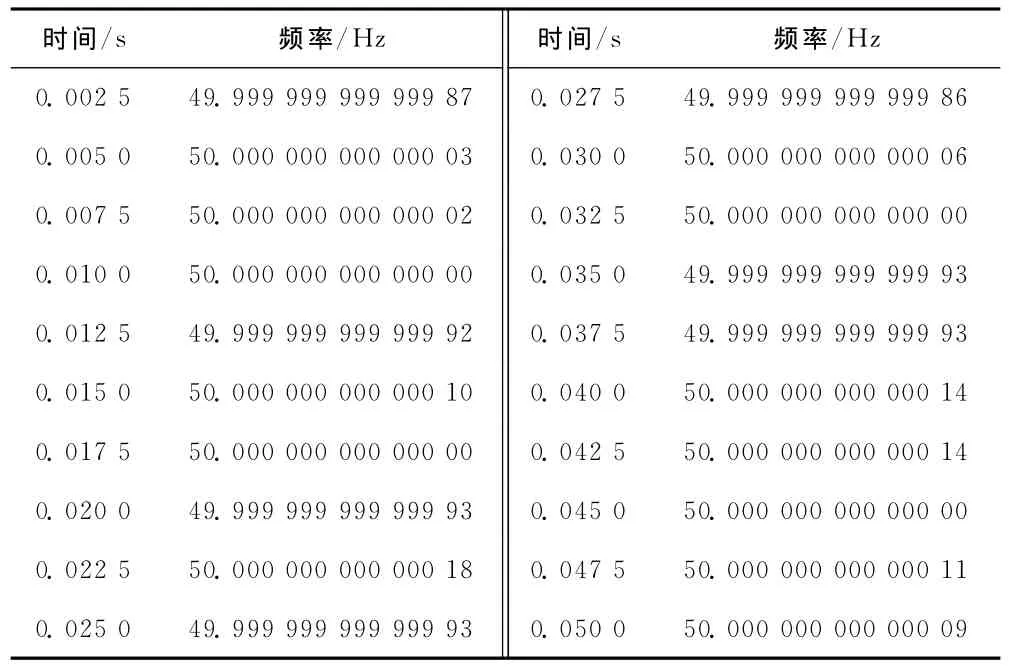
表1 不同时刻所对应的瞬时频率

图4 基波相位图仿真

3 结语

通过Matlab和CCS得出的仿真结果，软件算法设计的可行性得到了验证。

图5 基波频率

［1］刘毅，孙莹光，杜祥岭．FFT算法在电力监控计算中的应用［J］．辽宁工学院学报，2001（4）

［2］赵永秀．基于SRFFT算法的电力系统谐波分析的研究［D］．西安：西安科技大学，2003