基于激励补偿机制的电动汽车充电站规模优化
2014-12-20芦杨雷霞吴泓俭杨毅徐贵阳
芦杨,雷霞,吴泓俭,杨毅,徐贵阳
(西华大学 电气信息学院,四川 成都 610039)
电动汽车具有污染小、噪音低、能源利用效率高等特点,大力发展电动汽车产业,能够减少我国对石油资源的依赖,保证国家的能源安全[1-3]。电动汽车的普及能够缓解生态环境恶化,实现节能减排,是人类经济社会可持续发展的重要保障。近年来电动汽车需求量持续增长,预计到2020年我国电动汽车的渗透率在10%左右[4-5],但其增长速度仍属缓慢。如能制定有效的激励补偿机制,将使电动汽车的推广速度得到有效提升,早日实现电动汽车的普及。
目前为止,大量文献对电动汽车的研究主要针对其能够产生的好处如:削峰填谷[6]、降低电网损耗[7]、为系统提供辅助服务[8]等进行。文献[9]对众多文献的电动汽车充电控制策略进行了总结论述。在涉及充电成本时,文献[10]以最小化电力零售商的购电成本制定充电策略,不仅涉及实时电价和负荷之间的关系,还涉及负荷预测。文献[11]至文献[13]均以最小化客户成本来制定充电模型。同时,有部分文献对用户充电电价或供电侧成本进行费用优化,对于激励政策仅提出激励概念,并无具体手段将其实现[14]。在充电站规模优化上文献[15]针对集中型充电站接入的电网规划问题,综合考虑电力网络和交通网络因素,建立了集中型充电站的定址分容模型。文献[16]以充电站成本最小化为目标考虑了充电站的选址定容问题。而文献[17]以充电站成本与网损费用之和最小为目标的充电站最优选址及定容。
基于上述考虑,本文在一电动汽车用户相对固定的区域(PHEV用户约1.5万),以用户充电费用和充电代理商充电成本为目标建立确定充电站规模的多目标优化模型。用户充电成本考虑了充电电价、误工及环保补偿额度,并对实际充电功率与调度计划充电功率的偏差实施惩罚。充电站代理商服务成本考虑了对用户支付误工补偿及环境价值补偿的同时加入了充电站初始建设的折算成本。利用NSAG-II算法求解得出了多种充电站规模建设的优化方案。最后,采用日前申报信息互动机制对电动汽车进行优化调度,并通过算例仿真验证所建模型的有效性。
1 用户侧电价模型建立
1.1 排队理论基本原理
排队理论(queuing theory),或称随机服务系统理论,是通过对服务对象及服务时间的统计研究,得出等待时间、排队长度、忙期长短等计量指标的统计规律,然后根据这些规律来改进服务系统的结构或重新组织被服务对象,使得服务系统既能满足服务对象的需要,又能使机构的费用最经济或某些指标最优。
1.2 充电设施服务指标

充电服务系统状态(稳态)的平衡方程[18]为:

由递推关系可以求得系统状态概率为:

相应地,系统的运行指标为:系统服务强度

用户平均等待时间

用户在充电站的逗留时间

再来车辆可能等待的概率

1.3 误工补偿费用模型
对用户接入充电设施充电前时段进行补偿,用Pw表示:

式中,Cw、Cb分别为误工费用和每分钟误工补偿额度,Cb 电动汽车接入充电设施服务系统期间,需支付充电电费为充电功率与对应时段电价之和的乘积。表示如下: 式(8)中,Mi表示第i辆电动汽车充电功率大小,为恒功率;Xi表示第i个充电桩开始充电时刻;P(t)为时段电价。式(9)中Tc,i表示为第i辆电动汽车充电时长;SOCi、CSi分别表示将在第i个充电桩充电的电动汽车电池剩余电量值和电池充电速率。 偏差惩罚电费由两部分组成:第一部分若电动汽车接入服务系统充电时段,整个充电站实际负荷功率值超过调度中心分配的功率范围则在该时段充电的电动汽车均需要支付额外的惩罚电费。表示如下: 式中,Cp为负荷功率偏差量转换为经济指标系数;Pm,t为第m个充电桩t时段的实际充电功率;[Dmin,m,t,Dmax,m,t]为充电站分配给第m个充电桩t时段的负荷功率区间。 用户在充电期间,相较于申报充电时段提前或滞后离开充电站,同样需承担一定惩罚费用,额度大小根据偏差百分比确定: 式中,θ表示偏差百分比转换为经济指标系数;Dm,t表示电动汽车用户离开充电站时电池电量百分比;Sm,t表示电动汽车用户日前申报时电量需求百分比。 根据式(10)、(11)求得电动汽车在充电时段内的偏差量并支付相应的偏差惩罚费用。建立该机制便于引导用户在用电低谷时段遵守充电时段规则进行充电。 在研究环境价值补偿时,假设电动汽车对象统一为本文所采用的BMW MINI E混合型动力电动汽车参数如下: 功率损耗(kW·h·km-1) 0.14最大里程/km 250充满电用时/h 3最大时速/(kW·h-1) 152容量/kW·h 35可用容量/kW·h 31.5电池类型 Li-ion 参考电力工业污染环境价值标准[19]、国四排放标准以及充电电价相对于成品油价格节约的费用建立了环境价值补偿模型。表1是电力工业污染物环境价值标准。 表1 电力工业污染物环境价值标准Tab. 1 Electricity industry standard of environmental pollutants 元/kg 表2取自国四排放标准。 表2 国四排放标准Tab. 2 State IV emission standards 电动汽车使用电力以替代成品油,则二者之间在能量转换方面存在如下关系: 式(12)表示使用汽油的汽车一次加油量能够产生的动力能量。其中,Qg为汽油热值,单位为kW·h,一般情况下Qg=5.68·107J/L;ηm为发动机效率取40%;C为加油量。通过式(13)可以求得与一次加油量所产生能量相等的电量。式(14)中,ω为节约电能补贴比例(%);Ve为表1中的环境价值标准值;Qe为使用成品油情况下产生的电能;Qc为实际充电电能。式(14)求得环境补偿支出额度Pe,其为充电较于加油所节约费用中的一定比例与相应环境价值额度对电动汽车用户进行补贴。 根据排队理论及各不同费用模型可以建立用户充电费用优化的目标函数为: 对于接受充电服务的用户而言,充电需要等待的时间越短,满意度越高。对于相同的等待时间,对用户给予补贴的用户满意度高于无补贴时。本文定义用户满意度。 根据西南某市一充电站实际调研得知电动汽车充电站建设成本构成,其中包括充电站构架成本以及充电站充电费用等。基于该调研,建立了一充电站成本折算模型: 式中,NC为充电桩个数;Cc为充电站建设、维护成本折算至电站开始运营时刻的成本,525 600·Y为服务年限内的分钟数,其中Y为服务年限。通过式(17)可以求得充电站每分钟的服务成本。 用户获得的环境及等待补偿补贴由政府及用户车型厂商通过充电站代理进行支付,支出费用额度模型如下式 式中,Cw·Ws为充电站对电动汽车用户支付的等待补偿额度。充电站服务成本优化的目标函数为: 随着电动汽车产业的发展,越来越多的电动汽车需要并入电网,大规模具有随机特性的负荷必然会对电力系统的安全、稳定造成影响。由此,一个具有提前预定功能的充电策略有利于降低大规模电动汽车入网对电网的冲击。 考虑日前申报的充电策略核心思想是基于排队理论,将电动汽车充电用户通过提前预定功能,使得充电站根据用户申报充电时段的不同进行充电安排。本文所搭建的调度模型架构如图1所示。 图1 充电策略流程图Fig. 1 Flowcharts of charging strategy 流程具体制定步骤如下: 步骤1:调度中心根据不同地区电动汽车用户数量的比例对各个Aggregator(简称AGG)代理商制定次日各时段充电站负荷要求。同时,电动汽车用户向AGG代理商递交次日充电申请(如充电量、到达时间等)。 步骤3:对接纳用户进行信息反馈,内容包括根据在充电站等待时间确定等待成本补偿额度及该时段充电电价情况。如用户接受反馈内容转至步骤4,反对则更换AGG代理商重复步骤1直至接受。 步骤4:次日实际充电,并根据实际充电情况支付充电费用、偏差惩罚费用并接受误工、环保补偿。 步骤5:根据不同时段的实际充电情况,得到全天充电情况并反馈至调度中心,调度中心根据某规则对负荷分配进行调整再分配至AGG代理商,重复数个周期后在满足调度中心负荷分配的情况下,用户和AGG代理商共同达到收益最优。 算法思想如图2所示。 图2 算法思想Fig. 2 Summary of algorithm 本文选取3个典型时段,每时段为1 h为例进行仿真。基本负荷为某地区电网实际数据[20-21],如图3所示。 图3 典型日负荷数据Fig. 3 Typical daily load curve 典型时段参考电价如表3所示。 表3 典型时段参考电价Fig. 3 Reference price of typical period 本文假设该生活区内电动汽车数量为1.5万辆,类型均为BMW MINI E;用户月均(按工作20天,每天8小时计)收入10 000元;电动汽车充电用户到达服从参数λ=3.2的泊松分布,每辆电动汽车接受充电服务的时间服从参数为μ=0.14的负指数分布,偏差惩罚经济指标θ取100,电能补贴比例ω取10%。文献[23]的研究以优化充电站充电桩个数,单纯考虑充电站以最快速度为该生活区的电动汽车用户提供充电服务时的结果表明:当生活区电动汽车用户为1.5万辆时,充电站的充电桩个数为32个最佳。当考虑到充电电价为实时电价、存在偏差惩罚费用且对用户有一定的误工及环保补偿费用时,我们选取研究对象充电桩的个数范围为25至39(对应方案类型1至15)。负荷偏差范围假设为调度中心给代理商分配功率上限为电网负荷历史最大峰值与固有负荷之差的二分之一,下限为固有负荷与电网负荷历史最小谷值之差的二分之一。 由随机产生的电动汽车充电用户到达情况,从时段1起始时刻接入充电站进行充电的电动汽车为20辆,充电时长为160 min,充电功率为9.5 kW,则当误工补贴额度Cw上限为最高时(与误工费相近)电动汽车用户充电费用与充电站服务成本优化结果如图4所示。 为了便于观察用户充电费用、代理商成本费用及误工补偿额度随充电桩个数(方案类型)的变化趋势,将优化结果示于图5中: 图4 补贴额度最大时EV充电费用与电站服务成本Fig. 4 The maximum subsidies optimization of cost for EV charging and charging station service 图5 费用及充电桩优化结果Fig. 5 Optimization of cost for EV charging and the number of charging piles 图5即补贴额度上限最大时的优化数据如表4所示。 表4 补贴额度上限最大时优化数据Tab. 4 Optimization of the maximum limit of subsidies 当误工补贴额度Cw上限为0时(即不采取补贴政策时)电动汽车用户充电费用与充电桩服务成本优化结果如图6所示。 图6 补贴额度最小时EV充电费用与电站服务成本Fig. 6 The minimum subsidies optimization of cost forEV charging and charging station service 同样为便于观察,将不采取补贴政策时的优化结果示于图7中。 图7 费用及充电桩优化结果Fig. 7 Optimization of cost for EV charging and the number of charging piles 图7即补贴额度上限最小时的优化数据如表5所示。 表5 补贴额度上限最小时优化数据Tab. 5 Optimization of the minimum limit of subsidies 用户满意度变化曲线如图8所示。 由仿真结果可知: 图8 用户满意度变化曲线Fig. 8 The curve of user’s satisfaction 1)当没有误工补偿且充电站规模较小时,由于考虑误工费,用户需要承担高昂的充电成本,用户满意度极低,反映出用户等待时长的不合理性。充电桩个数的增加,减少了用户充电前的等待时间,用户承担的误工费有所下降,使得用户充电费用减少。可以看出,当充电桩个数大于28个时,用户充电费用的变化趋于平缓,用户满意度有明显提升。充电代理商的成本随着充电桩个数的增加而逐渐递增,当大于35个充电桩时,成本递增比例有所增加而用户满意度趋于平稳,充电站收益递增比例减少。 2)当有误工补偿措施(最低0元/min,最高1.039元/min)且没有考虑用户等待时长的合理性时,充电桩个数对用户充电费用的影响并不明显,这是由于充电站支付的误工补偿弥补了用户大量等待时间的误工费用,从满意度曲线上可以看出虽然用户支付的费用相差不多,但满意度差异较大。随着充电桩个数的增加,减少了用户等待时间,充电费用下降,补贴措施对用户的充电费用影响逐渐减小。充电代理商的成本费用有所上升。 3)与无激励补贴措施时的充电费用比较,对用户给予一定的补偿,用户充电费用明显减少。而相较于传统汽车行驶250 km需支付200元左右的燃油价格(假设100 km耗油10 L),使用电动汽车所需的充电费用大大降低,更有利于电动汽车的推广普及。 4)由结论1)可知充电桩个数较少时(≤28),充电代理商成本费用较低,但此时用户等待时间很长,严重影响了用户充电的满意度,从而不宜采取此类方案。充电桩个数较多时(≥35),充电站成本过高,且对于用户满意度提升效果较差,需要相关政策对其进行鼓励方适宜采取。因此,在使得电动汽车用户与充电代理商收益同时最优时,有数种方案(28≤c≤35)可以根据实际情况如建站位置、建站规模进行选取,增加了选择的灵活性、经济性。 当采用考虑激励补偿机制的充电策略时,合理的补偿额度能够从经济角度引导用户选择电动汽车替代传统汽车,可以使得用户支付较低的充电费用取代以往的燃油费。与此同时,不同的补偿额度对代理商充电站的充电设施服务系统建设有不同的要求,从而影响充电站服务设施建设费用。相反,如果没有考虑激励补偿机制,则用户需要支付较高的充电费用,不利于电动汽车的推广普及且对电网产生较大的影响。 大力推广电动汽车的使用,从环境、经济、能源安全等方面都具有重大意义。有效的激励补偿措施能够有效加快电动汽车的普及进程。 另一方面,在一个城市规划建设相对成熟的,在任意区域满足用户需求的充电站并非一件简单的事情。 在此背景下,本文建立了考虑误工及环境补偿措施的电价激励机制优化模型。通过优化得到了数类最优方案,在为充电用户和充电代理商提供最佳收益的同时,为有充电站规模限制的地域提供了具有更高选择灵活性的优化方案。 [1] TURKER H,BACHA S,CHATROUX D. Impact of plugin hybrid electric vehicles(PHEV)on the french electric grid[C]// Proceeding of Innovative Smart Grid Technologies Conference Europe,2010. [2] ROE C,MEISEI. J,OVERBYE T,et al. Power system level impacts of plug-in hybrid electric vehicles using simulation data[C]// Proceeding of IEEE Energy 2030 Conference,2008. [3] 钱科军,周承科,袁越. 纯电动汽车与电网相互关系的研究现状[J]. 电网与清洁能源,2010,26(11): 1-7.QIAN Kejun,ZHOU Chengke,YUAN Yue. A review of research on the interaction between fully electric vehicles and power systems[J]. Power System and Clean Energy,2010,26(11): 1-7(in Chinese). [4] SHAO Shuai. Electrification of transportation:a study of the electric vehicle industry in China[R]. Duke University,2011. [5] 罗卓伟,胡泽春,宋永华,等. 电动汽车充电负荷计算方法[J]. 电力系统自动化,2011,35(14): 36-42.LUO Zhuowei,HU Zechun,SONG Yonghua,et al. Study on plug-in electric vehicles charging load calculating[J].Automation of Electric Power Systems,2011,35(14):36-42(in Chinese). [6] DENHOLM P,SHORT W. An evaluation of utility system impacts and benefits of optimally dispatched plug-in hybrid electric vehicles[R]. Colorado:National Renewable Energy Laboratory,2006. [7] 陈加盛,张建华,林建业,等. 以降低电网损耗为目标的电动汽车充电策略[J]. 电力系统及其自动化学报,2012,24(3): 139-144.CHEN Jiasheng,ZHANG Jianhua,LIN Jianye,et al.Strategies for electric vehicle charging with aiming at reducing network losses[J]. Proceedings of the CSU-EPSA.2012,24(3): 139-144(in Chinese). [8] WILLETT K,JASNA T. Vehicle-to-grid power fundamentals:Calculating capacity and net revenue[J]. Journal of Power Sources,2005,144(1):268-279. [9] 张志伟,顾丹珍. 电动汽车充电策略综述[J]. 上海电力学院学报,2012,28(4): 336-340.ZHANG Zhiwei,GU Danzhen. Electric vehicle charging tactics review[J]. Journal of Shanghai University of Electric Power,2012,28(4): 336-340(in Chinese). [10] DOOSTIZADEH M,KHANABADI M,ESMAEILIAN A,et al. Optimal energy management of a retailer with smart metering and plug-in hybrid electric vehicle[C]// Proceedings of the 10th International Environment and Electrical Engineering,2011. [11] 邹文,吴福保,刘志宏.实时电价下插电式混合动力汽车智能集中充电策略[J]. 电力系统自动化,2011,35(14):62-67.ZOU Wen,WU Fubao,LIU Zhihong. Centralized charging strategies of plug-in hybrid electric vehicles under electricity markets based on spot pricing[J]. Automation of electric Power Systems,2011,35(14): 62-67(in Chinese). [12] QIAN K,ZHOU C,ALLAN M,et al. Modeling of load demand due to EV battery charging in distribution systems[J]. IEEE Trans.on Power System,2011,26(2): 802-810. [13] ROTERING N,ILIC M. Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets[J].IEEE Trans. on Power Systems,26(3): 1021-1028. [14] 姚伟锋,赵俊华,文福拴,等. 基于双层优化的电动汽车充放电调度策略[J]. 电力系统自动化,2012,36(11):30-37.YAO Weifeng,ZHAO Junhua,WEN Fushuan,et al. A charging and discharging dispatching strategy for electric vehicles based on bi-level optimization[J]. Automation of Electric Power Systems,2012,36(11):30-37(in Chinese). [15] 高赐威,张亮,薛飞,等. 考虑集中型充电站定址分容的电网规划研究[J]. 中国电机工程学报,2012,32(7):40-46.GAO Ciwei,ZHANG Liang,XUE Fei,et al.Grid planning considering capacity and site of large scale centralized charging stations[J]. Proceedings of the CSEE,2012,32(7): 40-46(in Chinese). [16] 陈婷,卫志农,吴霜,等. 考虑电动汽车充电站选址定容的配电网规划[J]. 电力系统及其自动化学报,2013,25(3): 1-7.CHEN Ting,WEI Zhinong,WU Shuang,et al. Distribution network planning by considering siting and sizing of electric vehicle charging stations[J]. Proceedings of the CSU-EPSA,2013,25(3): 1-7(in Chinese). [17] 刘志鹏,文福拴,薛禹胜,等. 电动汽车充电站的最优选址和定容[J]. 电力系统自动化,2012,36(3): 54-59.LIU Zhipeng,WEN Fushuan,XUE Yusheng,et al. Optimal siting and sizing of electric vehicle charging stations[J].Automation of Electric Power Systems,2012,36(3): 54-59(in Chinese). [18] 韩中庚,实用运筹学模型、方法与计算[M]. 北京: 清华大学出版社,2007. [19] 魏学好,周浩. 中国火力发电行业减排污染物的环境价值标准估算[J]. 环境科学研究,2003,16(1):53-57.WEU Xuehao,ZHOU Hao. Evaluating the environmental value schedule of pollutants mitigated in China thermal power industry[J]. Research of Environmental Sciences,2003,16(1):53-57(in Chinese). [20] 吴秋伟,汪蕾,邹云. 基于DSM和MCP的分时电价的确定与分析[J]. 电力需求侧管理,2003,5(1): 24-29.WU Qiuwei,WANG Lei,ZOU Yun. Determination and analysis of TOU power price based on DSM and MCP[J].Power Demand Side Management,2003,5(1): 24-29(in Chinese). [21] 戴诗容,雷霞. 电动汽车峰谷分时充放电电价研究[J].电网与清洁能源,2013(29):77-82.DAI Shirong,LEI Xia. Study on electric vehicle charging and discharging TOU price[J]. Power System and Clean Energy,2013(29):77-82(in Chinese). [22] 苗轶群,江全元,曹一家. 含电动汽车及换电站的微网优化调度研究[J]. 电力自动化设备,2012,32(9):18-24.MIAO Yiqun,JIANG Quanyuan,CAO Yijia. Microgrid stochastic dispatch considering electric vehicles and battery swap stations[J]. Electric Power Automation Equipment,2012,32(9):18-24(in Chinese). [23] 李如琦,苏浩益. 基于排队论的电动汽车充电设施优化配置[J]. 电力系统自动化,2011,35(14): 58-61.LI Ruqi,SU Haoyi. Optimal allocation of charging facilities for electric vehicles based on queuing theory[J]. Automation of Electric Power Systems,2011,35(14): 58-61(in Chinese).1.4 充电费用及偏差惩罚电费模型


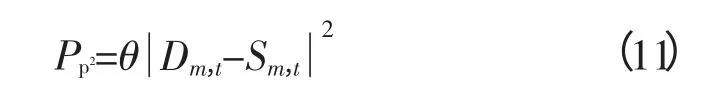
1.5 环境价值补偿模型




1.6 用户充电费用模型

1.7 用户满意度模型

2 充电站代理商侧模型建立
2.1 充电站成本折算模型

2.2 用户补偿支出模型

3 考虑日前申报情况的充电策略


4 仿真分析
4.1 仿真思想

4.2 算例仿真


4.3 仿真结果







5 结语
