ControlImp：生物系统可控性插件

袁 琴，李怀松，李建成，刘 娟

（武汉大学 计算机学院，湖北 武汉430072）

0 引 言

根据控制理论，一个复杂网络是否可控最终表现在当给定一组驱动节点时，网络能否在有限时间内从初始状态转换到预期状态。该定义符合人们对控制论直观的解释，通过对驱动节点进行适当的操控使其引导系统的行为向特定状态发展［1－6］。控制理论是工程学高度发展的分支，它应用于电路学、制造工艺、通讯系统［7，8］、航空航天等多个方面。控制论研究领域学者及研究人员相继提出了各种控制论算法，如部分完全可控、结构可控［4，9，10］、精确可控和epsilon精确可控等。

为了满足各领域对网络可视化不同需求，出现了种类、数量繁多的网络可视化工具，被广泛应用的有UCIENT、Cytoscape、Pajek等。其中Cytoscape是一个致力于为用户提供开源的网络显示和分析的软件，它为生物学研究者提供了良好的可视化环境和分析平台，同时由于它具有开源性和集成性，可以很方便地将其它网络分析算法整合其上，对其的运用提供很好的扩展。

尽管生物系统可控性和网络可视化的研究已经相当广泛，但是将两者结合的方法却不常见。本文设计了一个集成于Cytoscape3.0 的判断生物系统可控性以及网络可视化插件ControlImp，将生物系统可控性的研究引入到可视化的领域上来，为生物系统可控性理论的推广应用提供帮助。

1 控制理论

一般情况下，一个生物系统有多个平衡状态，其中一个平衡状态表示生物体的正常状态，其余的代表非正常（疾病）状态。令ynormal表示正常状态，yabnormal表示非正常状态。当给定一组驱动节点时，能否在有限时间内将生物系统从yabnormal状态控制到ynormal状态作为生物系统是否可控的判断标准。生物系统的控制方程如式 （1）所示

式中：A——生物系统节点间相互作用矩阵，大小n×n，n为生物系统中节点数。向量x（t）＝ （x1（t），…xn（t））T表示当时间为t时n 个节点的状态，且x （0）为yabnormal和ynormal之间的差值。B 为驱动节点0－1矩阵，大小为n×p，且p≤n，bij＝1表示第j （j≤p）个控制变量作用到节点i（i≤n）上，反之bij＝0。u（t）＝ （u1（t），…up（t））T为控制输入向量，作用在驱动节点上，p 为驱动节点数。

1.1 精确可控理论

精确可控理论的判断，可以用两种方法，一种是利用控制矩阵C 来判断，另一种是利用矩阵Φf来判断。

矩阵C 的计算如式 （2）所示

矩阵Φf的计算如式 （3）所示

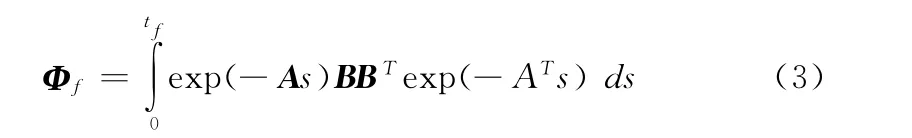
判断方法如下：

理论1：rank（C）＝＝rank（C，x0）是否成立，若成立，则生物系统可控，反之亦反。

图1为小网络的控制，利用精确可控理论1进行判断。控制论中边的方向与平常我们所理解的是相反的，图1中v3指向v1在矩阵A 中表示为a13。该小网络由控制输入向量u（t）＝ （u1（t），u2（t））T控制驱动节点v1、v3。计算可知rank （C）＝＝rank（C，x0），故网络可控，能够将网络由初始状态转换到预期状态。

理论2：rank（Φf）＝＝rank（Φf，x0）是否成立，若成立，则生物系统可控，反之亦反。

图1 小网络的控制

1.2 epsilon精确可控理论

对于某些系统是不能精确控制的，而且现实中数据是时有噪音的，因此可以引入epsilon精确可控理论。该理论的基本思路就是查看它是否可以把状态差值控制到0附近，而不是精确到0。

具体方法是判断式 （4）是否成立

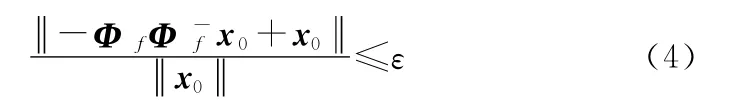
1.3 控制论结论

利用控制理论进行判断，如果生物系统可控，则控制输入节点状态值曲线和普通节点的状态值曲线计算方法如下：

控制输入节点状态值曲线如式 （5）所示

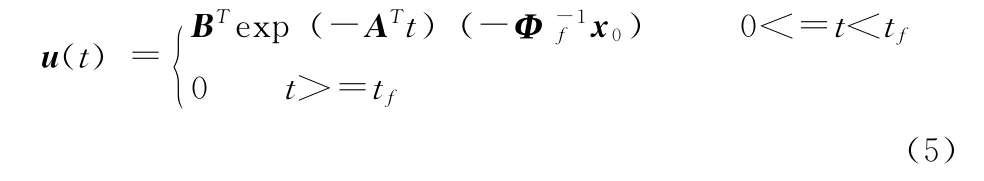
普通节点状态值曲线如式 （6）所示

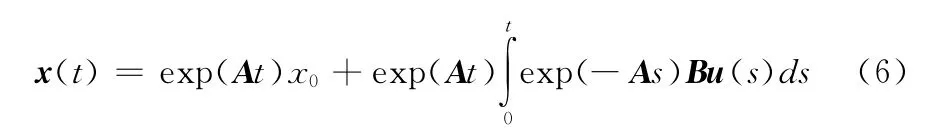
当控制输入向量u（t）＝ （u1（t），…up（t））T作用于驱动节点矩阵B 时，普通节点矩阵A 的状态值曲线x（t）最终趋于0，则可以判断生物系统是可控的，从而能够将生物系统从非正常状态状态控制到正常状态。

2 插件设计与实现

Cytoscape软件致力于为用户提供一个开源的网络显示和分析平台，软件主要提供了网络显示、布局、查询等方面的基本功能。在生物网络图中，节点代表基因、蛋白质等生物结构，节点之间的连接表示这些生物结构之间的相互作用。同时，Cytoscape3.0 软件具有开源性，可扩展等特性。Cytoscape3.0致力于创建一个模快化架构，它允许应用程序包含一系列子模块，并且每个子模块实现应用程序的部分功能。并且Cytoscape3.0拥有一套明确定义并简化的API接口，API接口与程序实现严格分离。从而Cytoscape软件的核心部分可以通过插件进行扩展，它允许程序员编写插件访问其核心数据结构并进行一系列操作。ControlImp即是一个扩展Cytoscape核心部分的插件。

2.1 功能描述

ControlImp插件实现对生物网络可控性分析和结果显示的功能。通过Cytoscape，用户可以在可视化环境下查看生物系统网络图、驱动节点以及各节点之间的相互作用关系，同时可以根据生物网络中各节点随时间变化的状态值曲线信息分析生物系统的可控性，还能将生物网络与功能注释数据链接在一起。

ControlImp插件的工作流程如下：Cytoscape3.0 启动后在Apps目录下加入ControlImp插件菜单项，插件启动后可以显示生物网络数据和驱动节点数据输入面板，以及控制论算法面板。若生物系统是可控的，则显示控制输入数据和生物网络数据网络图及曲线状态图。

2.2 插件结构

ControlImp插件结构如图2 所示，包括控制理论和结果显示两大部分组成。控制理论部分包含判断生物系统可控性的算法，由精确可控、epsilon精确可控组成，用于分析生物系统是否可控；结果显示部分包括生物系统网络图、驱动节点网络图、生物系统曲线图、控制输入曲线图，用于将结果可视化显示方便用户对生物系统进行分析和判断。

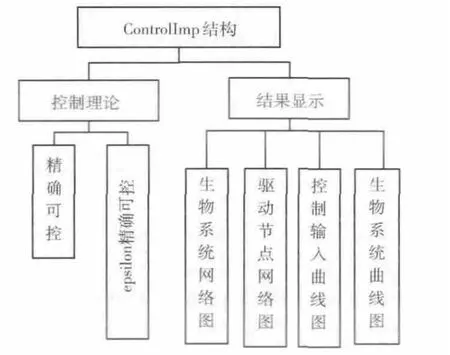
图2 ControlImp插件结构

2.3 插件设计及运行效果

在Cytoscape3.0下，Apps的子菜单App Manager用于管理插件，包括安装、删除、搜索、查看等功能。ControlImp通过App Manager进行安装，安装完成后在Cytoscape界面的Apps目录下可以看到ControlImp菜单，Con－trolImp子菜单包括Add File（network，driver）和ControlAlgorithm 菜单项，各菜单项功能分别为：Add File用于导入生物网络数据和driver数据；ControlAlgorithm 是控制论算法面板。效果如图3所示。

图3 ControlImp插件操作菜单

控制论算法面板用于选择控制论算法所需的各项参数，操作界面如图4所示。

图4 控制论算法面板

用户可以选择生物网络数据、driver数据、控制论算法，并且可以直接使用默认参数或自定义各参数值。当参数设定完成后，点击 “Run”按钮，对参数进行有效性验证，验证成功后按照用户选择的参数执行控制论算法。

图5为精确可控结果，其中t＝10。图5 （a）所示为生物网络图，其中深色节点表示驱动节点，浅色节点表示普通节点。当一个生物系统精确可控时，控制输入节点状态值曲线如图5 （b）所示，在图5 （b）中当t＞10时控制节点状态值曲线为0，普通节点状态值曲线如图5 （c）所示，在图5 （c）中当t＝10时，普通节点状态值曲线趋于0，从而可以证明生物系统是精确可控的。通过图5可知，当给定一组驱动节点时，生物系统最终能够趋于平衡状态，这正符合控制论精确可控结论。

图6为epsilon精确可控结果，令t＝1，epsilon＝0.15。图6 （a）所示为生物网络图，图6 （b）为控制输入节点状态值曲线，图6 （c）为普通节点状态值曲线，在图6 （c）中当t＝1时，普通节点状态值曲线趋于0附近，从而可以证明生物系统是epsilon精确可控的。通过图6可知，当一个生物系统epsilon精确可控时，给定一组驱动节点，生物系统状态差值最终能够控制到0附近，这正符合控制论epsilon精确可控结论。

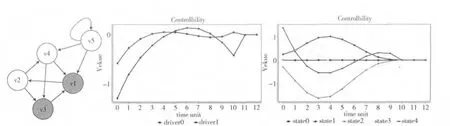
图5 精确可控结果

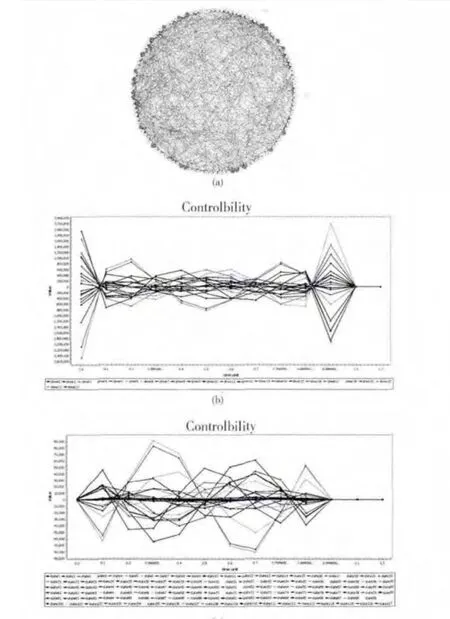
图6 epsilon精确可控结果

3 结束语

集成于Cytoscape3.0的用于判断生物系统可控性以及网络可视化的ControlImp插件利用控制理论研究任意复杂有向网络的可控性，并找出一组合适的驱动节点用于在有限时间内将网络控制到平衡状态，同时，它将网络结果进行可视化显示对于该理论的应用具有很强的推动作用，进一步促进生物系统可控性的研究、应用和推广。插件中的可控性算法可以不断的更新和扩展，并能够对不同的可控性算法进行分析和比较，该插件能够成为判断生物系统可控性和可视化的有效工具。

［1］Liu YY，Slotine JJ，Barabasi AL.Control centrality and hierarchical structure in complex networks ［J］.PloS ONE，2012，7 （9）：e44459.

［2］Sorrentino F，di Bernardo M，Garofalo F，et al.Controllability of complex networks via pinning ［J］.Physical review E，Statistical， Nonlinear，and Soft Matter Physics，2007，75：046103.

［3］Lombardi A，Hornquist M.Controllability analysis of networks［J］.Physical review E，Statistical，Nonlinear，and Soft Matter Physics，2007，75：056110.

［4］Liu YY，Slotine JJ，Barabasi AL.Controllability of complex networks［J］.Nature，2011，473 （7346）：167－173.

［5］Egerstedt M.Complex networks：Degrees of control［J］.Nature，2011，473 （7346）：158－159.

［6］Wang WX，Ni X，Lai YC，et al.Optimizing controllability of complex networks by minimum structural perturbations ［J］.Physical review E，Statistical，Nonlinear，and Soft Matter Physics，2012，85：026115.

［7］Key PB，Massoulie L.Control of communication networks：Welfare maximization and multipath transfers［J］.Philosophical Transactions Series A，Mathematical，Physical，and Engineering Sciencesm，2008，366：1955－1971.

［8］Briggs K，Kelly F，Smith M Preface.Modelling and control of transport and communication networks ［J］.Philosophical Transactions Series A，Mathematical，Physical，and Engineering Sciences，2008，366：1877－1878.

［9］Nacher JC，Akutsu T.Structural controllability of unidirectional bipartite networks［J］.Scientific reports，2013 （3）：1647.

［10］Cowan NJ，Chastain EJ，Vilhena DA，et al.Nodal dynamics，not degree distributions，determine the structural controllability of complex networks ［J］.PloS one，2012（7）：e38398.