受电弓空气动力对列车弓网特性的影响仿真

杨 康，黄焯麒，于 龙，陈唐龙

（西南交通大学 电气工程学院，四川 成都610031）

0 引 言

随着高速铁路的迅速发展，电气化列车的运行速度越来越快，高速气流产生的空气动力对列车运行的影响越来越大。目前研究主要集中在列车空气动力特性及其与列车和周围环境相互影响的方面［1］，高速列车受电弓空气动力学效应对弓网动力学性能的影响研究并不多。所谓弓网受流，是指电气化列车在运行过程中，通过安装在车顶的受电弓与道路上空的接触网悬挂系统之间的滑动接触，获取电能来驱使列车运动的过程。受电弓良好的空气动力性能是保证弓网受流质量的重要因素。当前对弓网动力学的研究很多，但是大多没有考虑空气动力的影响［2－4］，这在列车低速运行时是可以的，但在高速情况下受电弓的空气动力特性，尤其是受电弓受到的空气抬升力对弓网关系的影响至关重要。

对受电弓空气动力性能的研究主要通过2种方法：风洞 实 验［5－7］和 数 值 计 算［8，9］。风 洞 实 验 所 需 的 成 本 高，数 值计算方法没有考虑受电弓的真实结构，很难得到准确的结果。随着计算机技术的发展，通过计算机仿真的方法研究受电弓的空气动力特性成为一种快速有效的方法。本文采用有限体积法结合N－S方程和连续方程，建立了受电弓的实体模型，分析了受电弓在不同车速下受到的空气动力特性；建立了弓网动态耦合的有限元模型，分析了受电弓空气抬升力对弓网动态特性的影响。

1 模型的建立

1.1 受电弓空气动力学模型

高速列车在以空气为介质的空间中运行，研究对象可归纳为研究空气流体以及在空气流体中的刚体间相互作用力的问题。在空气动力学研究中，忽略流体系的份子结构，将流体看作是连续介质，其中不存在真空、分子间无间隙和分子运动。由于流体的连续性，将流体的运动学得各个基本量 （速度、压力等）看作是某些物理量 （时间、空间坐标）的连续函数，用连续函数的数学模型求解空气动力学问题。

建立高速受电弓的简化模型，如图1 所示。受电弓运行的计算区域的长为22m，宽为12m，高为5m。由于受电弓结构复杂，计算区域用非结构网格进行离散，受电弓表面为三角形网格，空气区域为四面体网格。考虑到距离受电弓越远的区域对计算结果的影响越小，采用渐变方式进行网格划分。受电弓表面的网格划分比较密集，网格大小为10 mm；离受电弓越远的区域，网格越稀疏，流场最外层网格大小为500～600 mm，如图2所示。

图1 受电弓简化仿真模型

图2 受电弓计算区域网格划分

不考虑环境风对列车的影响，在列车运行速在160 km／h到350km／h时，对应的马赫数小于0.3，空气的压缩性可以不考虑。受电弓周围空气场一般可以看做为定常、等温、不可压缩的三维流场，通常具有较高的雷诺数，应按湍流处理［1］。采用标准k－ε 模型来模拟湍流模型，其方程为［10］

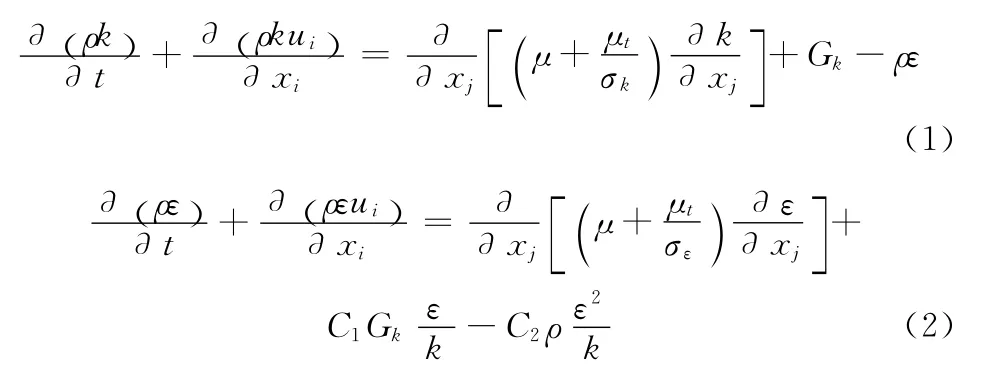
其中

式中：ρ——空气密度；k——湍流动能；ε——湍流耗散率；xi或xj——坐标的3个分量，分别代表x，y，z 这3个方向坐标；ui或uj——列车周围流场速度，分别代表ux，uy，uz这3个坐标方向的速度分量；μ——流体的黏性系数；C1，C2——经验常数；σk，σε——分别为湍流动能和湍流动耗散率对应的普朗特数。

根据气体黏性应力与气体运动速度之间的关系，运用牛顿第二定律，忽略空气的质量力，得到直角坐标系下不可压缩黏性流体的3 个运动方程，即不可压缩流的N－S方程

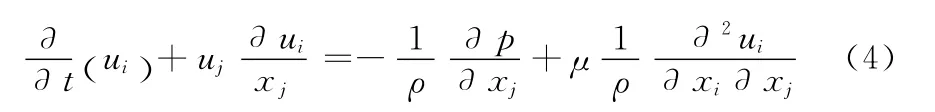
受电弓周围流体运动遵循质量守恒定律，可得到连续方程

1.2 受电弓—接触网系统模型

接触网采用简单链形接触网，由承力索、接触线、吊弦、线夹以及定位器等组成，是一个复杂的机械系统。受电弓由上框架、下框架、弓头等结构组成。这样的系统很难做出其真实的模型，通常对其模型进行简化。承力索和接触线的有限元模型采用欧拉－伯努利梁，吊弦采用弹簧单元。受电弓采用三元质量块单元。弓网耦合系统的模型［11］如图3所示。

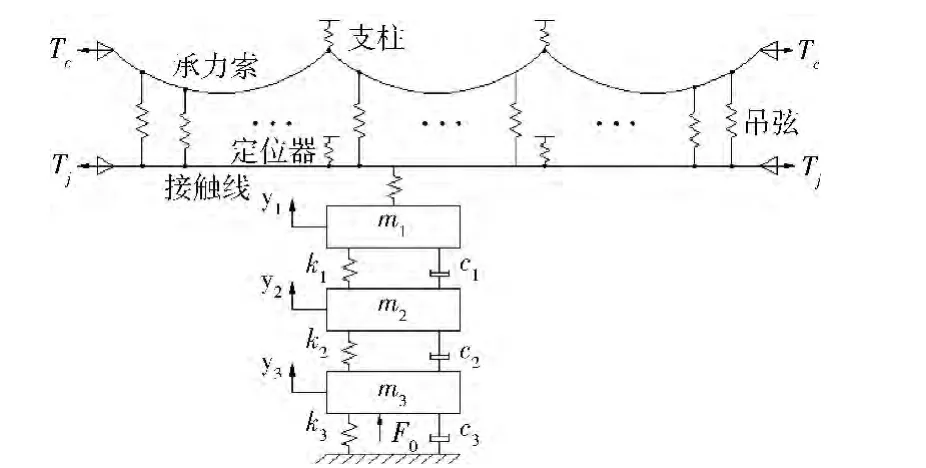
图3 弓网仿真模型

图3中，Tc是承力索的张力；Tj是接触线的张力；m1、m2、m3分别是受电弓弓头、上框架和下框架的等效质量；k1、k2、k3分别是弓头与上框架、上框架与下框架、下框架与机车顶部之间的等效刚度；c1、c2、c3分别是弓头与上框架、上框架与下框架、下框架与机车顶部之间的等效阻尼；y1、y2、y3分别是弓头、上框架和下框架的位移；F0是受电弓的静态抬升力。

弓网耦合系统的运动方程可简写为矩阵形式［2，12］

式中：［M］——弓网系统的质量矩阵；［C］——弓网系统的阻尼矩阵；［K］——弓网系统的刚度矩阵；［F］——外载荷矩阵；y——位移矩阵。受电弓和接触网的仿真参数见表1和表2。

表1 受电弓模型参数

表2 接触网参数

2 仿真结果与分析

2.1 受电弓空气动力特性仿真

将受电弓计算区域的顶面和侧面设置为滑移壁面；受电弓表面和地面设置为无滑移壁面；出口截面设置为压力出口边界；入口截面设置为速度入口边界，速度值为列车的运行速度。

利用FLUENT 流场计算软件，采用标准k－ε模型来模拟受电弓周围的空气流场，流场中的控制方程可用公式（1）～式 （5）来描述，仿真迭代800次，计算得到受电弓开口运行时各部件的气动阻力和气动升力。图4显示的是车速350km／h情况下受电弓所受的阻力和升力在迭代运行过程中的变化情况。从图中可以看出，迭代约400 次后，受电弓受到的空气阻力和升力趋于稳定。整弓的阻力稳定在902.2N 左右，升力稳定在49.3N 左右。受电弓的阻力与列车的运行方向相反，阻碍受电弓的前行，是受电弓产生气动噪声的主要来源；受电弓的升力方向垂直于路面，使受电弓框架和弓头产生垂向的振动，影响受电弓－接触网之间接触受流的质量。

图4 受电弓空气特性仿真

不同速度情况下，受电弓开口运行各部件所受到的空气动力值如表3所示。由表3可知，受电弓弓头由于结构复杂，所受的阻力最大；上下臂杆的空气升力大小相近，方向相反，基本能够相互抵消，受电弓受到的空气升力主要来自于弓头。由此可知，受电弓的弓头是空气动力的主要受力部件。

表3 开口运行时受电弓各部件的气动力／N

受电弓整弓的气动阻力和气动升力随着速度的增加而增大，与速度的平方成正比，如图5所示。受电弓的静态抬升力为70N，当运行速度为160km／h时，整弓的升力约为11.5 N，是静态抬升力的16.4%；而速度达到350 km／h时，整弓的升力达到49.4 N，是静态抬升力的70.7%。因此，在高速条件下的弓网受流，必须考虑受电弓空气升力的影响。

2.2 弓网动态仿真

图5 受电弓空气动力与速度的关系

利用ANSYS软件建立弓网耦合仿真模型，如图6 所示。计算弓网接触压力时，只有垂向的作用力才能对其产生影响，因此只需考虑受电弓空气抬升力的作用。分别将受电弓各部件的气动升力加载于受电弓三元质量块的相应位置，通过弓网耦合动力学仿真计算得到车速为350km／h时的弓网接触压力。图7 给出了考虑 （虚线）和未考虑（实线）受电弓气动升力情况下接触压力的比较。由图可知，考虑受电弓气动升力的影响后，接触力明显增大，且接触力的波动性也增大。

图6 弓网仿真模型的建立

表4为考虑和未考虑受电弓气动升力作用时的接触压力数据比较。由表可知，考虑受电弓气动升力后，接触力的平均值增加了19.5N，最大值增加了42.2N，最小值和标准差均有增加。可见受电弓的气动升力对接触压力的影响在高速时十分的明显。

图7 空气升力对弓网接触压力的影响

表4 接触压力数据比较

3 结束语

本文利用流体分析软件仿真计算了受电弓在高速运行时的空气动力特性，并在考虑受电弓空气动力的情况下，对弓网动态接触压力进行了分析，主要得到以下两点结论：

（1）仿真计算了受电弓运行时，周围空气场对受电弓的空气动力特性。结果表明，受电弓所受到的空气阻力和升力随速度的增加而增大，与速度的平方成正比，高速情况下的弓网受流，必须考虑气动升力的影响。其中弓头是主要的受力部件。

（2）分析了高速情况下受电弓空气升力对弓网接触压力的影响。结果表明空气升力增大了弓网接触压力，且接触力的波动性也增大，使得弓网受流质量变差。

［1］TIAN Hongqi.Train aerodynamic［M］.Beijing：China Railway Press，2007 （in Chinese）. ［田红旗.列车空气动力学［M］.北京：中国铁道出版社，2007.］

［2］ZHOU Ning，ZHANG Weihua.Dynamical performance simulation of the pantograph－catenary coupled system based on direct intergration method ［J］.China Railway Science，2008，29（6）：71－76 （in Chinese）.［周宁，张卫华.基于直接积分法的弓网耦合系统动态性能仿真分析 ［J］.中国铁道科学，2008，29 （6）：71－76.］

［3］ZHAO Fei，LIU Zhigang，ZHANG Xiaoxiao.Simulation of high－speed pantograph－catenary system dynamic performance based on finite element model［J］.Journal of the China Railway Society，2012，34 （8）：33－38 （in Chinese）. ［赵飞，刘志刚，张晓晓.基于有限元的高速弓网系统动态性能仿真研究［J］.铁道学报，2012，34 （8）：33－38.］

［4］Cho YH，Lee K.Influence of contact wire pre－sag on the dynamics of pantograph－railway catenary ［J］.International Journal of Mechanical Sciences，2010，52 （11）：1471－1490.

［5］CAI Guohua.The experimental technique of pantograph of super express train in low speed wind tunnel［J］.Journal of Railway Engineering Society，2006，4 （94）：67－70 （in Chinese）.［蔡国华.高速列车受电弓低速风洞试验技术 ［J］.铁道工程学报，2006，4 （94）：67－70.］

［6］ZHANG Jianhui，YANG Jiong，YAO Yong.Wind tunnel test investigation on pantograph drag reduction of high speed train［J］.Journal of Railway Science and Engineering，2010，7（6）：116－121 （in Chinese）.［张建辉，杨炯，姚勇.高速列车受电弓减阻的风洞试验研究 ［J］.铁道科学与工程学报，2010，7 （6）：116－121.］

［7］Bocciolone M，Resta F.Pantograph aerodynamic effects on the pantograph－catenary interaction ［J］.Vehicle System Dynamics，2006，44 （S1）：560－570.

［8］YANG Zhen.Study on current collection of high－speed pantograph based on aerodynamic ［J］.Electric Railway，2009，3：17－20 （in Chinese）.［杨桢.基于空气动力学的受电弓高速受流研究 ［J］.电气化铁道，2009，3：17－20.］

［9］TIAN Hongqi.Study on the characteristics of train air resistance under wind environment ［J］.China Railway Science，2008，29 （5）：108－112 （in Chinese）.［田红旗.风环境下的列车空气阻力特性研究 ［J］.中国铁道科学，2008，29 （5）：108－112.］

［10］ZHU Hongjun，LIN Yuanhua，XIE Longhan.Fluent12fluid analysis and engineering simulation ［M］.Beijing：Tsinghua University Press，2011 （in Chinese）.［朱红钧，林元华，谢龙汉.Fluent12流体分析及工程仿真 ［M］.北京：清华大学出版社，2011.］

［11］Zhou Ning，Zhang Weihua.Investigation on dynamic performance and parameter optimization design of pantograph and catenary system ［J］.Finite Elements in Analysis and Design，2011，47 （3）：288－295.

［12］Simon Walters.Simulation of fuzzy control applied to a railway pantograph－catenary system ［C］／／Proceedings of the 14th International Conference on Knowledge－based and Intelligent Information and Engineering Systems：Part II，2010：322－330.