多视角下的改进ICP算法

姚亚盼，韩 燮，况立群，韩慧妍

（中北大学 计算机与控制工程学院，山西 太原030051）

0 引 言

为了解决很多物体的表面无法在同一视角下进行观察的问题，很多学者对多视角下物体的三维重建进行了研究，其中，对于得到的三维点云数据的配准［1］是一个研究热点。点云的自动配准主要包括粗配准和精确配准2 个部分［2］，粗配准的目的是为精确配准提供良好的初值，缩小相邻点云之间的旋转误差和平移误差。精确配准［3］是用来找到最合适的旋转矩阵和平移矩阵，使得相邻点云配准的误差最小。

最近点迭代 （iterative closest point，ICP）算法自1992年由Besl和Mckay提出之后便在自动配准方面得到了广泛的引用。但是由于传统的ICP 算法效率并不高，而且对初始值要求很高，容易陷入局部收敛等缺陷，很多学者对ICP算法进行了改进。文献 ［4］在考虑曲率相似的基础上建立了角度、距离约束，然后利用三点旋转平移变量法求解配准参数；文献 ［5］利用基于曲率的方法进行抽样加速配准效率，但由于噪声的影响，基于曲率特征的点云配准方法鲁棒性并不高；文献 ［6］在考虑点曲率相似度的基础上，引入新的匹配点对度量准则；文献 ［7］利用法向量内积加权，但是由于人工标记特征点对影响了配准的精度和效率；文献 ［8］提出了一种基于邻域特征的配准方法；文献 ［9］利用了Delaunay 三 角 剖 分 改 进ICP 算 法；文 献［10］提出了一种距离约束改进的迭代邻近点算法。

本文通过对目前国内外点云配准算法进行分析，做出如下改进：

（1）在点云重合部分提取时，提出了一种新的基于Delaunay的改进方法。利用Delaunay三角剖分对相邻点云不重合的部分进行了剔除，该方法对于点云数据的获取方法及精确度没有要求，适用范围较为广泛。

（2）利用三角面片重心与物体重心之间的距离将点云数据进行分类配准。

1 目前ICP算法流程

ICP （iterative closest point）算 法 即 最 近 点 迭 代 算 法，该算法在点云配准中有良好的适用性，总体来说，可分为6个步骤：

（1）数据的选择。提取相邻两组所有的点云数据，分别记数据点云为X＝ ｛x1，x2，...，xm｝，模型点云为Y＝｛y1，y2，...，yn｝。数据点云X 中的数据点的个数为m，模型点云Y 中的数据点的个数为n，则要求m≤n。并且对于X 中的每一个点xi，都应在Y 中找到对应的yi。

（2）点云的匹配。即寻找数据点云和模型点云中最近似的对应关系。一般通过四元数法来给定初值并用K－D 树来加速寻找最近点云。设旋转变换向量为单位四元数qR＝［qx，qy，qz，qw］，并且＋＋＋＝1，平移变换向量为qT＝ ［tx，ty，tz］。数据点云X 与模型点云Y 的重心分别为

则利用四元数法与K－D 树相结合计算得到最佳旋转矩阵R（qR）与最佳平移向量qT

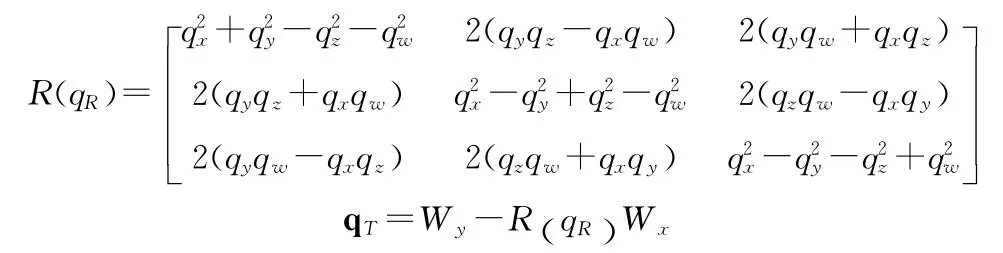
（3）计算已配对的各组点的权重值。一组点的权重值是根据它们的法向量来确定的。假设已配对两点的法向量分别为nx和ny，则权重值

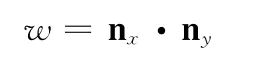
若考虑两点间的距离来计算加权值，则

式中：distmax——所有点对之间的最大距离。

（4）错误点的拒绝。由于两组点云只有部分重合，所以一般将包含边缘的点都去除，主要有根据Delaunay三角化和曲率的方法来去除错误点。

（5）误差的度量。计算相对应的一组点的误差

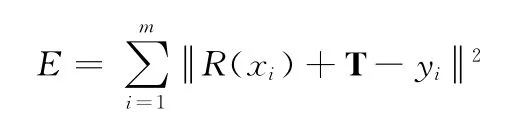
式中：R——3×3的旋转矩阵，T——平移向量。

（6）最优化。ICP 算法通过多次迭代上述步骤使得误差最小化。利用得到最小误差的旋转矩阵R 和平移向量T将数据点云与模型点云进行配准。

2 改进的ICP算法

本文利用Delaunay三角剖分对点云的重合部分进行提取，然后根据三角面片重心与物体重心之间的距离将点云数据进行分类，从而提高ICP算法的匹配精度。

2.1 点云重合部分提取

ICP算法要求数据点云必须完全包含于模型点云，由于在多视角三维重建的过程中得到的点云数据一般都是部分包含的，这样会有很多不重复的点，如果将所有的数据通过随机选取或者根据法向量抽样等方法直接进行选取，不但使数据配准结果不准确，而且因为计算了大量不必要的数据，导致算法效率降低。所以本文先对ICP 算法的第一步进行改进，通过利用获取数据时的数学关系以及Delaunay三角剖分来对原始点云数据进行精简。

记第一个视角下得到的点云数据为模型点云，第2个视角下得到的点云数据为数据点云，它们之间的旋转角度为θ，以球体作为被测物体进行说明，记球的半径为r，相机到球面的距离为d，相机的视角为φ，则几何关系如图1所示。

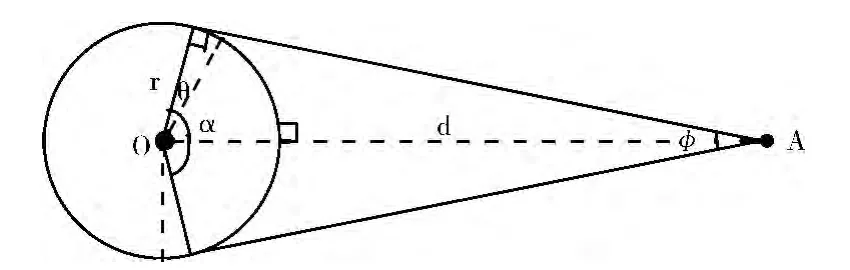
图1 几何关系

当角度转过θ时，物体发生变化的表面积占相机可视范围内的表面积的百分比η

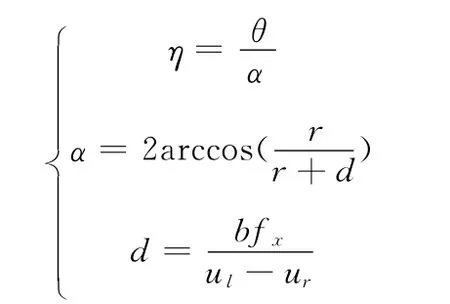
其中，ul－ur称为视差值，b 为两相机基线，fx为相机在相机坐标系u 轴方向的有效焦距。综合以上三式，易求出百分比η。提取重合部分点云时便要根据η来去除不重合的点云。

由于多个视角下，物体的点云数据并不是在所有的边缘处都不重合，如图2所示，左图中的边界点A 在右图中的A′的位置。而B 点到了右图的边界B′处。故要利用点云的三维坐标以及Delaunay 三角剖分来提取可匹配的点云数据。

图2 两组点云数据不重叠部分

对2个视角下得到的点云数据都进行Delaunay三角剖分，由于Delaunay三角化是指在每一相邻Voronoi区域中，将散乱点之间加上线段后得到的嵌入到平面中的图，所以首先要画出Voronoi图，而Voronoi图是由一系列连接两邻近点直线的垂直平分线组成的连续多边形，故可知Voronoi图中每个交点都是某一个三角形的外接圆圆心，即每个三角面片的重心。在三角化时，有很关键的一步就是如何判断一个点是否处于边界位置，本文利用三角化时求得的三角面片的重心与相邻的三角面片的重心的比较次数来判断，因为如果某个点所处的三角形的重心都与周围的三角形的重心的比较次数为3，则这点一定不是边界点，若有不是3的，那么该点就是边界点。

通过建立三颗二叉排序树，将点云的3 个坐标值X，Y，Z 分别进行排序，得到Xmax，Xmin，Ymax，Ymin，Zmax，Zmin，根据三维坐标值的范围可以确定如图2所示的要抛弃的点云的坐标值的范围。

结合该范围对利用Delaunay三角剖分后找到的边界点进行百分比为η 的点云数据的删除，这样可以减少不匹配的点云的数量，降低迭代时无效的点云所占的比例，提高配准效率与精度。

对于不规则物体的三维点云，原理类似，不同的是，要首先求得该物体的重心O （x0，y0，z0），计算点云数据中每点X （x，y，z）到物体重心的距离

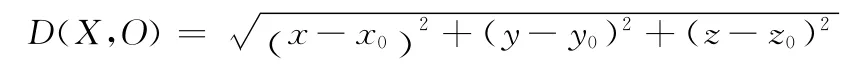
由于在剔除点云数据时，即使剔除掉少量可以配准的点云数据，对配准的结果几乎没有影响，所以只需求出Dmin。以它为半径，O 为球心做球，计算出最小的角度关系，进而求出百分比η即可。

2.2 点云数据分类配准

对于得到的三维点云信息，由于它只有三维坐标值，所以无法根据其拓扑信息、点云特征来进行配准。待测物体在旋转平台上旋转一个角度之后，它的表面并不发生变化，所以，相邻点云对应点由Delaunay三角剖分之后形成的三角形的重心到该物体的重心的距离是相等的。

在2.1中已经提到了Delaunay三角剖分时因为要求出边界点所以会计算每一个三角面片的重心，因此可以计算出各三角面片的重心与物体重心的距离，求得Dmax，Dmin。设定初始间隔值，根据该值将D 划分为M 个范围，将每个距离范围内的点云进行迭代配准，求出每个范围内所得到的最优旋转矩阵Rpart和平移向量Tpart，则旋转矩阵R 和平移向量T 为

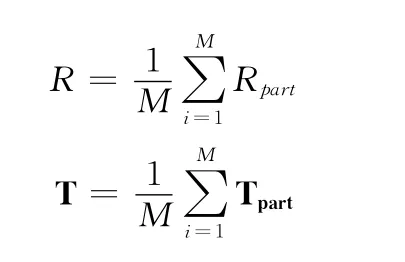
3 实验步骤

实验设备：双目相机、棋盘格和旋转平台［11］，如图3所示。

图3 实验设备

3.1 点云采集

（1）利用基于棋盘格的平面模板法对双目相机进行标定，获得相机的内外参数。

（2）将待测物体放到旋转平台上。

（3）利用双目相机采集该视角下的彩色图像，并进行校正。

（4）进行立体匹配，得到左视图的视差图。

（5）经过点的重建得到三维点云数据。

（6）利用遥控器令转盘按照固定的角度10°旋转，获取下一个视角下的数据。

（7）重复 （3） （4） （5） （6）步，直到旋转到350°停止。

左右视图如图4所示，视差图如图5所示。

图4 左右视图

3.2 局部配准

利用改进的ICP算法对点云数据Xi＋1与其相邻组点云数据Xi进行点云重合部分提取及分组，由于对点云数据已经进行过Delaunay三角剖分，故以R0，T0为初值，根据点到面的方式来计算最小误差E

图5 视差图

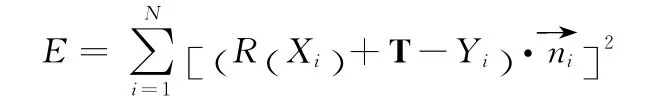
式中：ni——在第i个模型点处的法向量。计算采集到的点云数据Xi＋1与Xi之间的旋转矩阵R 和平移向量T。

3.3 全局配准

实验得到的36 组数据记为Xi＝ ｛x1，x2，...，xn｝，其中i＝0，…，35。以X0，即0°时的点云数据坐标为参考坐标，将X1到X35的点云数据都变换到0°时的坐标下。根据相邻点云数据之间的旋转平移关系

可以推导出各组点云数据到0°时的旋转矩阵R＊和平移向量T＊，其中Ri＋1、Ti＋1分别表示第i＋1组点云数据变换到第i组点云数据坐标下的旋转矩阵和平移向量。

（1）当i＝0时，即X1旋转到X0时，有

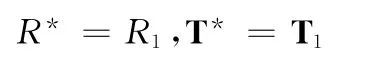
（2）当i≥1时，即Xi＋1旋转到X0时，有

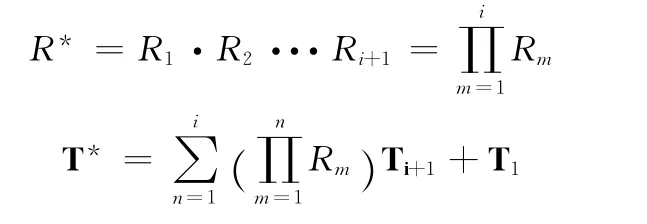
4 实验分析

本文实验的硬件环境为NVIDIA GeForce 9600GT，4 G 内存。软件环境为Windows 8 64 位操作系统、MATLAB2013。以实验得到的0°和10°时台灯的点云数据为例进行局部配准，点云数据如图6所示。

由图7可以看出，本文改进的ICP 算法进行局部配准时的点云数据有所减少并且配准效果更好。但是由于局部配准点云数量相对较少，所以效果不是很明显。

通过对比改进前后的ICP 算法，可以看出改进之后减少了配准时的点云数目并提高了配准效率，见表1。

图6 0°和10°时台灯的点云数据

图7 改进前后局部配准对比

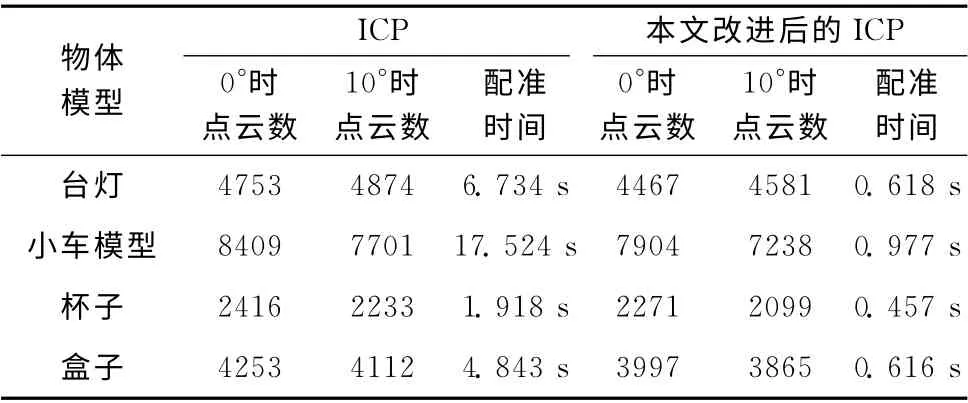
表1 算法改进前后配准效果对比

全局配准时，点云数据很多，所以效果比较明显，利用改进前后的ICP算法进行局部配准之后又进行全局配准的对比效果图如图8所示。

图8 全局配准效果对比

本文利用改进后的ICP 算法分别对形状规则的物体：杯子、盒子以及形状不规则的物体：台灯、小车模型进行全局配准，效果如图9所示，可以看出改进的算法配准效果不错。

图9 全局配准效果

5 结束语

本文利用Delaunay三角剖分对相邻点云不重合的部分进行了剔除，提取出相邻点云重合部分；并利用三角面片重心与物体重心之间的距离将点云数据进行分类配准，改进了ICP算法，通过对形状较为规则的物体 （杯子、盒子）和形状不规则的物体 （台灯、小车模型）进行实验验证，得到了良好的配准效果，本文算法提高了传统ICP 算法的配准效率和配准精度。但是，对于物体比较尖锐或较细长等点云较少的部分配准效果并不好，还需继续改进。

［1］LI Huaize.Multiple－view 3Dreconstruction method based on turntable［D］.Zhejiang：Zhejiang University，2013：30－33（in Chinese）. ［李怀泽.基于旋转平台的多视角三维重建［D］.浙江：浙江大学，2013：30－33.］

［2］DAI Jinglan，CHEN Zhiyang，YE Xiuzi.The application of ICP algorithm in point cloud alignment［J］.Jorunal of Image and Graphics，2007，12 （3）：517－521 （in Chinese）. ［戴静兰，陈志杨，叶修梓.ICP算法在点云配准中的应用 ［J］.中国图像图形学报，2007，12 （3）：517－521.］

［3］WEI Qiming，WU Weiyong，DENG Changshou.Matching unorganized points data under different viewpoints based on improved evolution algorithm ［J］.Application Research of Computers，2010，27 （8）：3156－3158 （in Chinese）. ［魏启明，吴维勇，邓长寿.基于改进的差异演化算法的多视角离散数据配准［J］.计算机应用研究，2010，27 （8）：3156－3158.］

［4］XU Jinting，LIU Weijun，SUN Yuwen.Algorithm for freeform surface matching based on curvatures ［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2007，19（2）：193－197 （in Chinese）. ［徐金亭，刘伟军，孙玉文.基于曲率特征的自由曲面匹配算法 ［J］.计算机辅助设计与图形学学报，2007，19 （2）：193－197.］

［5］Hans Martin Kjer，JakobWilm.Evaluation of surface registration algorithms for PET motion correction ［D］.Denmark：Technical University of Denmark，2010：30－31.

［6］XUE Yaohong，LIANG Xuezhang，MA Ting，et al.An automatic registration method of scanned point clouds［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2011，23（2）：223－231 （in Chinese）. ［薛耀红，梁学章，马婷，等.扫描点云的一种自动配准方法 ［J］.计算机辅助设计与图形学学报，2011，23 （2）：223－231.］

［7］SUN Qian，HE Mingyi.Clouds model in 3Dreconstruction［J］.Computer Simulation，2011，28 （11）：218－221 （in Chinese）.［孙谦，何明一.三维重建中点云模型与纹理图像的配准 ［J］.计算机仿真，2011，28 （11）：218－221.］

［8］HE Yongxing，OU Xinliang，KUANG Xiaolan.Application of neighborhood feature in point cloud registration ［J］.Journal of Computer Applications，2012，32 （3）：762－765 （in Chinese）.［贺永兴，欧新良，匡小兰.邻域特征在点云配准中的应用 ［J］.计算机应用，2012，32 （3）：762－765.］

［9］JIANG Chengcheng，HU Tongsen，ZHOU Wei.An improved iterative closest points algorithm ［J］.Computer Systems ＆Applications，2009，18 （8）：84－87 （in Chinese）. ［蒋成成，胡同森，周维.一种改进的迭代最近点算法 ［J］.计算机系统应用，2009，18 （8）：84－87.］

［10］ZHANG Lei，JI Zhihang，PU Jiexin，et al.ICP method improved by constraints for point cloud registration ［J］.Computer Engineering and Applications，2012，48 （18）：197－200（in Chinese）.［张蕾，冀治航，普杰信，等.约束改进的ICP点云配准方法［J］.计算机工程与应用，2012，48 （18）：197－200.］

［11］LIU Xin，XU Huarong，HU Zhanyi.GPU based fast 3D－object modeling with Kinect ［J］.ACTA Automatica Sinica，2012，38 （8）：1288－1297 （in Chinese）. ［刘鑫，许华荣，胡占义.基于GPU 和Kinect的快速物体重建 ［J］.自动化学报，2012，38 （8）：1288－1297.］