基于约束分析的RapidIO 路由选择算法

李宗灿，曹 建

（中南大学 物理与电子学院，湖南 长沙410083）

0 引 言

RapidIO 总线技术是专门针对高性能嵌入式系统芯片间和板间互连通信而设计的，该互连技术支持各种拓扑结构，通过交换器件可组成各种规模大小的通信网络。同时作为高速总线技术，RapidIO 总线对网络的延迟、带宽及丢包率等服务质量参数 （quality of service，QoS）有着很高的要求，因此研究如何提高RapidIO 网络的服务质量有很重要的现实意义［1］。

RapidIO 网络的服务质量问题是一个多混合约束度量问题，在给定的多种混合约束条件下寻找可行的路径，是一个NPC问题，应采用启发式算法进行求解［2］。文献 ［3，4］提出采用改进的遗传算法进行可行路径的选择，但该算法存在编码困难等问题，且遗传算法为局部搜索算法，容易陷入局部极值导致找不到可行解；文献 ［5］提出基于K－shortest算法，在寻径过程中用模拟退火跳出局部最优，该方法具有很好的全局最优解，然而该算法性能非常依赖于温度和节点存储路径的影响。针对这种情况，本文提出约束严苛度的概念，并在此基础上设计基于K 最优路径的RapidIO 路由选择算法。该算法采用约束严苛度表示不同系统对QoS的不同需求，并采用基于K 最短路径的搜索算法进行搜索，最终选择满足约束要求的可行路径。仿真结果表明，该算法有较高的搜索成功率，同时具有多项式时间复杂度，因此有很好的实用价值。

1 RapidIO 网络模型

1.1 RapidIO 网络结构

RapidIO 总线是基于包交换的传输协议，包是RapidIO协议中基本的传输单位。如图1所示，RapidIO 网络通常由2种器件构成，分别是终端器件和交换器件。终端器件是各种处理器节点，是数据包的源端或目的端，在网络中作为数据交换的发起方或接收方；交换器件通常不发起请求包，其作用是根据内置路由表，将包含不同目的ID 的数据包传送到不同的端口。

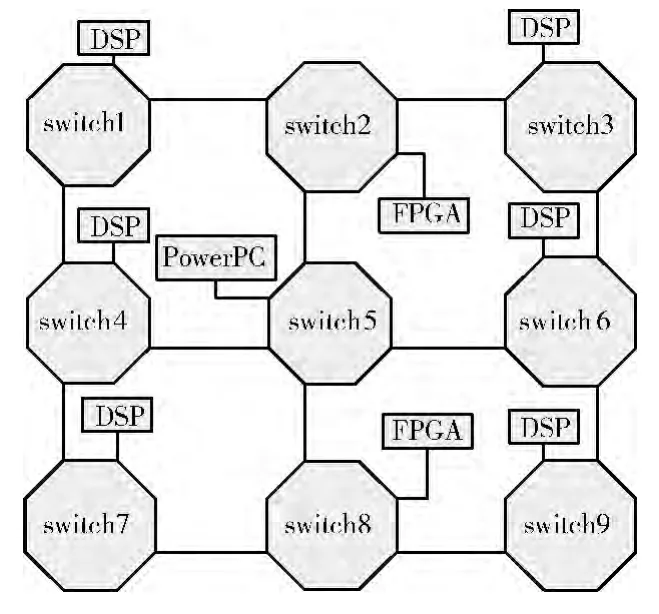
图1 某系统RapidIO 结构框架

1.2 QoS模型

RapidIO 网络QoS问题通常包括跳数、时延、带宽和丢包率等约束条件，因此是多混合度量参数路由问题。QoS研究通常分为2个方向，一是满足多约束的可行路径选择，一是满足多约束的最优路径选择，两者都是NP 完全问题。本文关注第一类QoS问题。

路由选择的目的就是要找出满足所有约束条件的可行路径。将RapidIO 中路由选择问题进行抽象，可以得到其通用的数学模型。

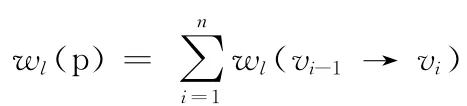
2 算法设计

2.1 算法思想

对一个约束可行的路径，往往对另一个不成立，求解满足多个QoS约束的路径是NP 完全问题，不具有多项式的复杂度，必须采用启发式算法。在目前提出的算法中，算法H＿MCOP［6］提出费用函数来统一多个约束之间的关系，并通过两次Dijkstra算法来预测前向路径，但是前后两次查找都可能陷入局部最优，导致找不到可行路径。算法DS＿MCP提出采用模拟退火算法跳出局部最优解，可以有很好的全局收敛性，然而模拟退火算法性能对于温度和迭代次数有很强的依赖性，并不能保证求得可行路径。

不同系统对QoS参数的约束要求是不同的，通过分析约束信息，可以有效的指示可行路径的搜索范围，在减小的范围空间内进行可行路径的搜索会大大提高搜索成功率并减少搜索次数［7］。

我们知道，不同的系统对于QoS参数有着不同的需求，会提出各种不同的QoS约束参数。如某些系统更追求低时延，对于带宽或其他服务质量并没有特别需要，则会对时延设置严格约束参数；某些系统对带宽看重，对时延并没有严格要求，那么系统的带宽约束必定非常严格。根据不同的系统需求，我们提出约束严苛度的概念。

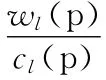
从定义中可以看出约束严苛度有以下几个特点：

（1）若路径p满足某项QoS约束条件，则该项约束严苛度csl（p）≤1，若csl（p）＞1，则路径p不满足该项QoS约束条件；

（2）在csl（p）≤1时，当csl（p）值越接近1，那么路径p的该项QoS约束裕量越小，约束越严苛；

（3）对于（1≤l≤k），若csl（p）≤1都成立，则路径p为满足QoS约束的可行解。

在此基础上，我们设计算法如下：

（1）针对k项不同约束度量，根据Dijkstra最短路径算法，依次计算其在该项约束度量下的最短路径，所有k种约束度量的最短路径总数为k条，分别记作p1，p2，…，pk；

（2）根据得出的最短路径，依次计算每条路径在相应的约束度量下的约束严苛度，分别记作cs1（p1），cs2（p2），…，csk（pk）；

（3）判断上述约束严苛度，若存在任一约束严苛度值大于1，则判断该网络不存在可行解，算法结束，否则进入下一步；

（4）若所有约束严苛度值都不大于1，则选择约束严苛度值最大的路径pm，则pm是在约束度量m 下得到的最优路径。分别计算路径pm的所有k项约束严苛度csl（pm），（1≤l≤k）。若路径pm的约束严苛度值存在大于1的情况，则进入下一步执行，否则pm即为可行解，算法结束；

（5）在第m 项度量约束条件下，采用文献 ［8，9］中的求解第K 最短路径的方法，计算次优解路径，判断该路径的第m 项约束严苛度，若不大于1，则进入下一步执行，否则判断无可行解，算法结束；

（6）计算上一步得到的路径的所有约束项严苛度，当该路径有约束严苛度值大于1，则转入上一步执行，否则该路径即为可行解，算法结束。

2.2 算法分析

在算法步骤 （1）中，提出采用Dijkstra算法求取最短路径，此处所说的最短路径是广义上的最短路径，即在单约束条件下的最优路径，如对于时延、跳数等约束，则为寻找最短路径，可直接通过Dijkstra算法寻找；对于带宽则为寻找最大带宽路径，可以通过修改最短路径算法得到，分别用求极大值和求极小值运算代替Dijkstra算法中求极小值运算和加法运算即可；对于丢包率则为寻找最小丢包率路径，也可以通过修改最短路径算法得到，将Dijkstra算法中求极小值运算和加法运算分别用求极大值和乘法运算代替就可得到，应注意在算法过程中丢包率到成功率的转换。Dijkstra算法的时间复杂度是O（n2），其中n为网络中节点的个数，算法步骤 （1）时间复杂度为O（kn2），其中k为约束条件的个数。

在算法步骤 （4）中，选取约束严苛度最高的约束度量进行后续第K 最优路径的计算，约束严苛度高表明系统更重视该约束条件，且满足该约束的路径数量相对更少，可以非常有效的减少后续算法的计算次数。

在算法步骤 （5）、步骤 （6）中，采用文献 ［8，9］中方法求解K 最短路径，最坏情况下其时间复杂度为O（Kn2），其中K 为第K 短路径，K 根据约束条件自适应产生。所以整个算法的时间复杂度为多项式复杂度，同时，因为算法中提出了对无可行解情况的判断和算法退出条件，因此在求解问题时，能够及时停止运算，降低路由计算的盲目性，具有很高的时效性。

该算法通过约束严苛度这一概念对系统约束条件进行评价，在该评价基础上将相互无关的多约束问题转化为有选择性的约束问题进行求解，可以快速寻找到可行解。同时该算法对于约束度量参数的增加也具有很好的扩展性。

2.3 算法应用

在图1所示系统中为每条边添加如下度量信息，为与别的算法进行比较，因此采用2个加性度量，则图1所示系统的拓扑结构如图2所示。

对于图2，设源节点为v1，目标节点为v9，给定QoS约束条件为C（24，24），通过观察可以发现可行路径为p＝v1－v4－v5－v6－v9，然而当采用H＿MCOP 算法进行计算时，找不到可行路径，因为该算法路径由前向和后向2个路径组成，在约束严苛情况下，一旦有一个路径陷入局部最优解，则找不到最终可行路径。

图2 系统拓扑

采用本文所提出算法，计算过程如下：

（2）比较可得约束度量2约束严苛度较大，因此以约束度量2作为侧重约束进行计算，计算p2 所有约束度量w（p2）＝（26，24）并不满足约束条件，因此采用第K 最优路径法［7］，求解约束度量2的次优路径保存在p2。

（3）求得次优路径p2＝v1－v4－v5－v6－v9，计算其约束度量w（p2）＝（16，24），可以满足约束条件，因此算法结束，可行解为p2＝v1－v4－v5－v6－v9。

在此问题中，若不采用约束严苛度进行方向判断，当采用K 最短路径求解时，K＝4才能求出可行解，约束严苛度的评判加速了可行解的查找。

3 算法性能测试

本文分别设计实验进行仿真，并与目前性能较好的H＿MCOP算法和DS＿MCP 算法作对比，同时测试在多次测量过程中所需要求解的第K 最优路径参数情况。

3.1 实验参数

（1）本实验使用Matlab产生N 个节点的完全随机拓扑图，为每个链路设置了在 ［1，100］区间内均匀分布且相互无关的k种约束度量wl（e），分别模拟了节点数为50，100，150，200的随机网络，每种情况产生10 个拓扑图，本文选取k＝2进行仿真。

（2）约束条件的设置对于问题是否有可行解有着决定性作用，本文依据3种方法产生约束条件。

C1：cl（p）＝wl（p），（1≤l≤k），路径p是用第1个约束参数计算出来的最优路径，若最优路径有多条，则在这些路径中取第2个约束参数最优的路径，从而保证路径p的唯一性。

3.2 性能评价

（1）成功率［10］，在节点数为50，100，150，200 的网络上分别随机选取1000对源－目标节点对，对每个网络计算路由成功率，并对10个同规模拓扑的成功率取均值。

（2）K值，由于本文采用了基于K 最短路径的算法，K值的大小决定算法耗费时间，也是算法评价的一个重要标准。

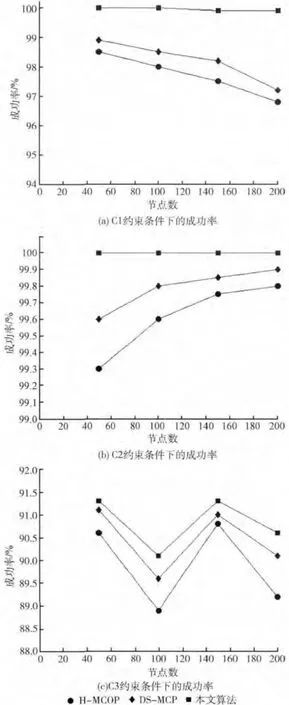
图3 3种不同约束下算法成功率比较

从图3中可以看出，在约束条件为C1 和C2，本文提出算法成功率要优于H－MCOP算法和DS－MCP算法。在约束条件为C3时，因为约束条件的随机变化，导致可行解是否存在不能保证，在相同的约束条件下进行测试，本文算法成功率也要优于H－MCOP 和DS－MCP。此处为保证DSMCP算法有最好效果，取M 为3，I为3。

当约束条件分别为C1，C2，C3 时，本文分别对本文算法和不采用约束严苛度的K 最短路径算法进行研究，对K 的大小进行了统计。结果见表1，表2，表3。

表1 C1约束下K 值比较

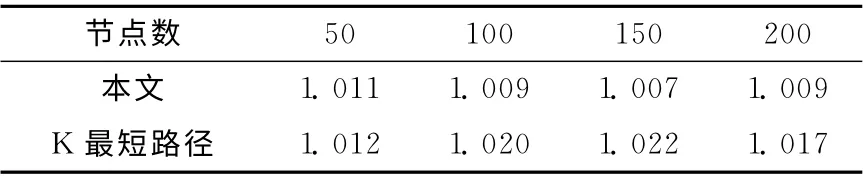
表2 C2约束下K 值比较

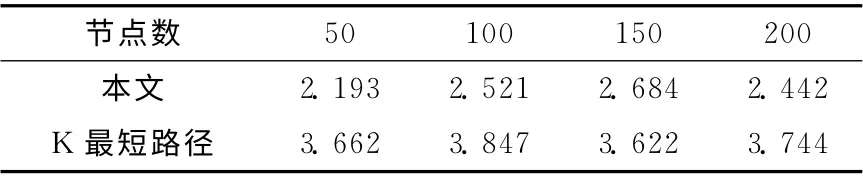
表3 C3约束下K 值比较

从上面3 个表格中可以看出，由于C1 约束下路径唯一，当采用约束严苛度进行搜索指引时，会大大减少K 最短路径求解次数，迅速找到可行解；C2约束非常宽松，在这种情况下约束严苛度影响不大；C3约束下本算法比K 最短路径的求解次数也有一定的减少。

通过上表可以看到，约束严苛度概念的引入，为算法后续求解K 最短路径提供了方向指导，尤其是在约束严格条件下，采用约束严苛度判别可以非常有效的减少K 最短路径的求解次数，从而大大减少了时间的消耗。

4 结束语

本文以多约束条件的RapidIO 网络路由选择问题为模型，定义了约束严苛度来表征系统对约束参数的需求，并通过约束严苛度指示搜索方向，避免了盲目搜索。在此基础上采用K－最优路径算法进行可行路径的搜索。本文所提出的启发性算法满足多项式复杂度，比以往算法有较高概率找到可行解，同时对于约束度量个数的扩展有着很好的适用性，因此具有很强的实用价值。

［1］PAN Ling，SANG Nan.Path distribution strategy in RapidIO network ［J］.Computer Applications，2008，28 （s2）：294－295 （in Chinese）.［潘灵，桑楠.一种RapidIO 网络路径分配策略 ［J］.计算机应用，2008，28 （s2）：294－295.］

［2］HAN He，QIN Yong.Overview of multi－constrained QoS routing algorithm ［J］.Computer Technology and Development，2012，22 （4）：133－136 （in Chinese）. ［韩贺，秦勇.基于多约束QoS路由算法综述 ［J］.计算机技术与发展，2012，22（4）：133－136.］

［3］CAI Wei，ZHANG Jiandong，CAI Huizhi.Optimization and improvement of RapidIO network routing strategy ［J］.Computer Engineering and Applications，2011，47 （14）：87－90（in Chinese）.［蔡炜，张建东，蔡惠智.RapidIO 网络路由分配策略的优化和改进 ［J］.计算机工程与应用，2011，47（14）：87－90.］

［4］CAI Wei，ZHANG Jiandong，CAI Huizhi.Multi－objective optimization of RapidIO network ［J］.Journal of Computer Applications，2010，30 （12）：3172－3175 （in Chinese）.［蔡炜，张建东，蔡惠智.RapidIO 网络QoS多目标优化 ［J］.计算机应用，2010，30 （12）：3172－3175.］

［5］ZOU Yonggui，WEI Lai.Optimal path algorithm with multiconstrained condition ［J］.Computer Applictions，2008，28（5）：1101－1103 （in Chinese）.［邹永贵，魏来.带多约束条件的最优路径选择算法研究 ［J］.计算机应用，2008，28 （5）：1101－1103.］

［6］QIAN Yi，QIAN Jin.Improved multi－constrained QoSR algorithm［J］.Computer Engineering and Design，2008，29 （8）：1931－1934 （in Chinese）.［钱奕，钱进.改进的QoS多约束路由算法［J］.计算机工程与设计，2008，29 （8）：1931－1934.］

［7］QI Xiaogang，LIU Lifang，LIU Sanyang.Multi－constrained path selection algorithm based on the depth of the distance vector［J］.ACTA Electronica SINICA，2009，37 （1）：175－179 （in Chinese）.［齐小刚，刘立芳，刘三阳.基于距离向量深度的多约束路径选择算法［J］.电子学报，2009，37 （1）：175－179.］

［8］FU Junwei，LI Xingming，CHEN Jie.A practical algorithm for finding the shortest Kth path based on deviation path ［J］.Computer Technology and Development，2009，19 （2）：120－126 （in Chinese）.［傅俊伟，李兴明，陈捷.基于背离路径的Kth最短路径使用搜索算法 ［J］.计算机技术与发展，2009，19 （2）：120－126.］

［9］BAI Yiduo，HU Peng，XIA Lanfang，et al.A kth－shortest path algorithm based on k－1shortest paths［J］.Geomatics and Information science of Wuhan University，2009，34 （4）：492－494 （in Chinese）.［白轶多，胡鹏，夏兰芳，等.关于k次短路径问题的分析与求解 ［J］.武汉大学学报：信息科学版，2009，34 （4）：492－494.］

［10］MA Yueyong，WANG Haimei，LIAO Jianjun.Comparative study of multi－constrained optimal path algorithms［J］.Journal of Nanjing University of Science and Technology，2011，35 （6）：749－754 （in Chinese）.［马跃勇，王海梅，廖建军.多约束最优路径算法比较研究 ［J］.南京理工大学学报，2011，35 （6）：749－754.］