基于神经遗传算法二级斜齿轮参数优化设计

冯顺利

FENG Shun-li

（河南交通职业技术学院 汽车学院，郑州 450005）

0 引言

齿轮减速器是一种常见的传动部件，在多种领域中已广泛应用。齿轮减速器设计中，减小齿轮尺寸和重量，延长齿轮使用寿命，提高承载能力和减少传动误差等是设计中需要重点考虑问题[1]。

二级斜齿轮减速器优化设计中，由于存在参数多、目标函数多、约束条件复杂等特点，一些简单的优化方法不易得到全局最优解；优化过程中，目标函数的权重系数的合理分配也是优化设计中的关键问题[2,3]。

遗传算法是一种借鉴生物界自然选择和生物遗传机制的一维随机搜索方法。传统的遗传算法对多目标优化中目标函数的权重分配不够合理。本文提及的优化算法引进敏感系数，利用神经网络算法对权重系数进行调整，在遗传算法优点的基础上解决了优化过程中权重系数不合理分配问题。

1 优化模型的建立

1.1 初始参数设置

二级斜齿轮减速器传动简图如图1所示。设计中，要求在满足齿根弯曲强度、齿面接触疲劳强度、运动不干涉和齿轮加工工艺要求条件下，对减速器纵向尺寸、接触疲劳应力差进行优化设计。

已知条件：输入轴转速n=1450r/min，输入功率P=4.2kW；总传动比i=25，齿宽系数φ=0.4，小齿轮比大齿轮宽b=4mm；大齿轮为20Cr，小齿轮为20CrMnTi。

图1 二级斜齿轮减速器传动简图

1.2 设计变量的选择

减速器斜齿轮的轴向尺寸由齿宽系数和齿轮分度圆直径决定，齿轮变位对设计目标影响较小，因此，取设计变量为Ⅰ级齿轮传动小齿轮齿数z1，标准法向模数m1，螺旋角β1，传动比i1，Ⅱ级齿轮传动小齿轮齿数z2，标准法向模数m2，螺旋角β2。

故设计变量取为：

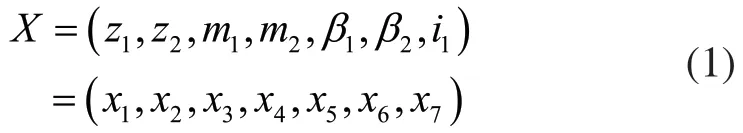
1.3 目标函数

1）纵向长度

由于齿轮轴向尺寸与分度圆直径存在线性关系，纵向长度尺寸可作为减速器体积和重量的较精确表述。因此，取纵向长度作为一个分目标函数，其表达式为：

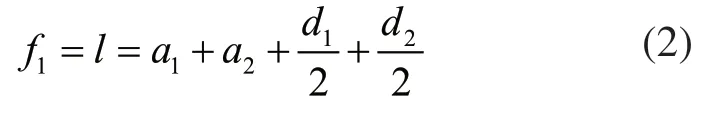
式中：a1为Ⅰ级齿轮中心距；a2为Ⅱ级齿轮为中心距；d1为Ⅰ级齿轮小齿轮分度圆直径；d2为Ⅱ级齿轮大齿轮分度圆直径。设计变量表示出的以纵向长度为目标函数的表达式为：

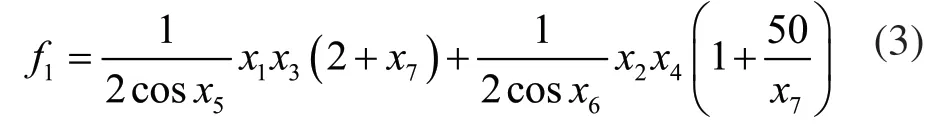
2）接触应力差

为了提高变速器寿命，减小齿轮加工成本，使两对齿轮等强度磨损，设计中将两级齿轮间接触应力只差作为一个分目标函数齿轮传动时齿面接触应力为：

式中：T为输入转矩；εα为端面重合度；KA为使用系数；KV为动载系数；KHα为齿间载荷分配系数；KHβ为齿向载荷分配系数；ZH为区域系数；ZE为弹性影响系数。若令K=KAKVKHαKHβ，Z=ZHZE，则目标函数可表示为：

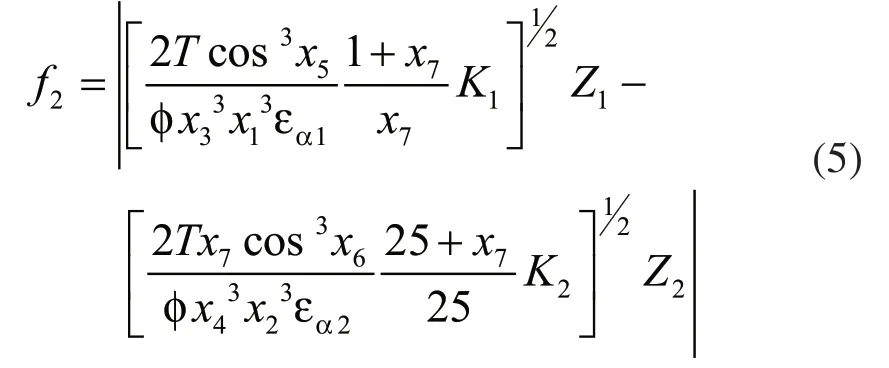
式中：K1、Z1为Ⅰ级齿轮传动综合影响系数；K2、Z2为Ⅱ级齿轮传动综合影响系数。

3）总目标函数

上述分目标函数之间相互影响，不可能同时达到最优，因此，构造总目标函数，总目标函数表达式为：

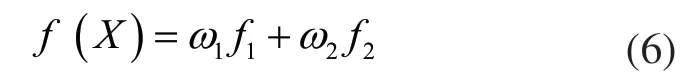
式中：ω1分目标函数纵向长度的权重系数；ω2为分目标函数接触应力差的权重系数。

权重系数的分配是多目标函数优化中的重要问题，合理的分配能同时延长齿轮的使用寿命和减小齿轮的加工成本，文中采用神经网络算法对权重系数进行调整，在遗传算法优化参数的同时合理调整权重系数，最终得到较合理的总目标函数及较优的设计参数。

4）归一化处理

分目标函数之间的量纲存在差别，优化时需将目标函数转化为无量纲的值。若设第k代分目标函数值为f1(k)、f2(k)；f1(k)max、f1(k)min分别表示目标函数f1在第1～k的最大和最小值，f2(k)max、f2(k)min表示目标函数f2在第1～k的最大和最小值，则归一化处理后f1、f2表达式为：

1.4 约束条件

1）设计变量范围设置

斜齿轮传动时，考虑一对齿轮等磨损因素，要求大小齿轮齿数互为质数；齿轮加工时为防止根切，要求小齿轮齿数大于17；齿轮齿数为一系列整数值；齿轮模数尽量在第一标准系列和第二标准系列中取值。综合上述因素，并结合斜齿轮传动特性和结构合理性，设置参数范围为：

1 7 ≤z1≤2 4,1 7 ≤z2≤2 4,2 ≤m1≤5.5，17≤m2≤24，5°≤β1≤35°，5°≤β2≤35°，3≤i1≤8。

2）齿面接触疲劳强度约束

式(4)为齿面接触疲劳强度的计算，在齿轮传动中，小齿轮的接触疲劳强度较高，但考虑大齿轮齿根点蚀因素，实际使用中许用接触应力为：

式中：[σH]1为小齿轮许用接触应力；[σH]2为大齿轮许用接触应力。齿面接触疲劳强度约束条件为：

3）齿根弯曲疲劳强度约束

齿根弯曲疲劳强度计算公式为：

式中：Yβ为斜齿轮螺旋角影响系数；YFA为斜齿轮齿形系数；YSA为斜齿轮应力校正系数。齿根弯曲疲劳强度约束条件为：

式中：σF1、σF2为小、大齿轮齿根弯曲疲劳应力；[σF]1、[σF]2为小、大齿轮许用弯曲应力。

4)不干涉约束

为防止Ⅰ级大齿轮齿顶与Ⅱ级齿轮轴相碰，设计时应满足：

式中：d12为Ⅰ级大齿轮齿顶圆直径；s为Ⅰ级大齿轮齿顶与Ⅱ级齿轮轴间距离。

2 算法简介

2.1 目标函数权重系数的调整

采用遗传算法优化参数的同时采用神经网络算法对多目标函数权重系数进行调整，在遗传算法优化过程中，参数的不同取值导致目标函数f1、f2的随之变化，设第k代目标函数f1的平均值与第k+1代f1的平均值差为△f1；同理，第k代目标函数f2的平均值与第k+1代f2的平均值差为△f2，若△f1＞△f2，则表明参数的变化能引起目标函数f1的较大变化，由此表明目标函数f1较目标函数f2重要，需对目标函数f1的第k代取值调整，调整表达式为：

式中：ω1(k)为第k代目标函数f1的权重系数；η为调整系数，η调整时采用BP神经网络，网络的输入为ω1和△f，输出为η；△f记为敏感系数。

敏感系数表征了优化参数的变化对目标函数f1的影响程度，即f1对参数变化的敏感程度，△f越大，f1受参数变化影响较大，f1的权重系数应适当增大。

2.2 算法流程

神经遗传算法具体流程如图2所示。

图2 算法流程图

3 优化结果及分析

设置遗传算法迭代次数为160，总目变函数f、分目标函数f1的权重系数ω1、分目标函数f1、分目标函数f2随迭代次数的变化关系如图3～图6所示。

图3 总目标函数随迭代次数变化

图4 权重系数ω1随迭代次数变化

图5 分目标函数f2随迭代次数变化

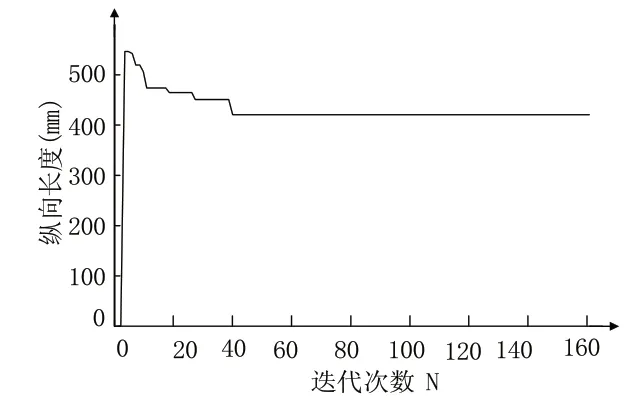
图6 分目标函数f1随迭代次数变化

由图4可知，权重系数ω1最佳取值为0.4755，此时，ω2=0.5245。权重系数的微小波动引起总目标函数的的微小波动，此时，f1基本不变，f2波动较大。若取ω1为0.4755，利用遗传算法进行二次优化，分目标函数f2随迭代次数变化关系如图7所示。

图7 二次优化下f2随迭代次数变化

由图7可知，权重系数一定时，f2最终达到最优值，优化结果如表1所示。

表1 优化方案与原方案参数对比表

由表1可知，优化前后，齿轮端面重合度变化不大，优化后比优化前纵向长度减少93mm，优化前Ⅱ级齿轮传动大齿轮齿数为88，小齿轮齿数为20，两齿数不互质，加快了齿轮磨损[6]。

4 结论

1）神经遗传算法是结合遗传算法和神经网络算法的优点，在利用遗传算法优势的基础上用BP神经网络对多目标函数的权重系数进行调整，能得到合理的权重分配。

2）引入敏感系数，将敏感系数应用于权重系数的调整中，使优化过程更为合理。

3）神经遗传算法可以应用到多参数、多目标、多约束的优化问题中，并能得到全局最优解。

[1]郑静,阎昌琪.基于复合-遗传算法斜齿轮减速器优化设计[J].应用科技,2010,37(10):21-25.

[2]何建成,张文明,罗婷婷.面向产品族的矿用自卸车轮边减速器设计[J].矿山机械,2013,41(1):25-29.

[3]张慧鹏.基于matlab的二级圆柱齿轮减速器优化设计[J].机械设计与制造,2010(4):79-80.

[4]席平原.基于神经网络的齿轮传动遗传算法优化[J].机械传动,2005,29(5):61-62.

[5]苏俊,席平原.基于神经网络的车辆主减速器混合遗传算法优化设计[J].机械设计与制造,2011(2):42-43.

[6]濮良贵,纪名刚.机械设计[M].北京:高等教育出版社,2007.