船舶推进轴系多体动力学和扭振特性

孙长飞，刘文科

(江苏海事职业技术学院，江苏 南京211170)

0 引 言

船舶推进轴系起着船舶动力传递的关键作用，轴系动力学性能的好坏直接决定着整个船舶的可靠性，甚至影响着船舶的航行安全［1-2］。例如:目前船舶发动机系统的主要故障源就是轴系因扭振现象的严重变形［3-4］，此外，扭振问题还可能导致包括曲轴、螺旋桨轴在内的多轴系的断裂、传动件的磨损、联轴器的失效和发动机噪声等问题的产生，严重影响着船舶的动力性能和航行安全性能［5-6］。

采用虚拟样机技术和多体动力学技术进行船舶推进轴系动力学特性分析具有计算过程高效、准确、工作效率高和设计周期大幅缩短等优点，成为目前研究的热点和难点［7］。国内外轴系扭振变形计算模型主要包括集总参数和质量沿轴线连续分布参数［8-10］两大类。集总参数模型将经离散化的轴系质量等效在惯性圆盘系上，圆盘之间用轻质弹性杆件相连，每个圆盘所受阻力来源与轴系内部和外部2个方面;质量沿轴线连续分布模型中轴系质量沿轴纵向连续分布，更符合实际情况。

本文在深入分析推进轴系扭振特性及其动力学理论的基础上，将在Solidworks 中建立的船舶推进轴系三维实体模型导入ADAMS 中形成轴系的多体动力学模型并对该模型进行不同工况下的扭振特性分析。

1 轴系扭振变形特性

轴系扭振的根本原因是统一轴系沿轴向不同坐标处重心不一致导致的扭转角不规则变化，如图1 所示。

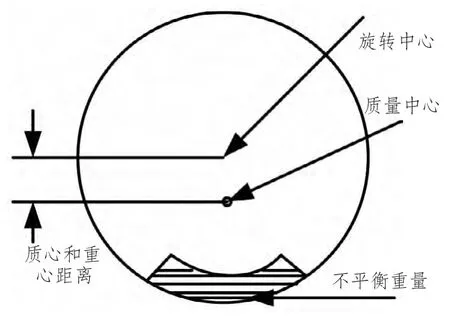
图1 船舶推进轴系扭振变形表示方法Fig.1 Deformation of ship propulsion shafting torsional vibration

假设在不平衡轴系上同时存在着力和力矩载荷，由牛顿定理可知，该轴系的振动状态方程如下:

式中:M 为广义质量矩阵;D 为阻尼矩阵;K 为刚度矩阵;q(t)为广义位移。若该轴系的振动自由度为n，则该轴系可分别表示为:

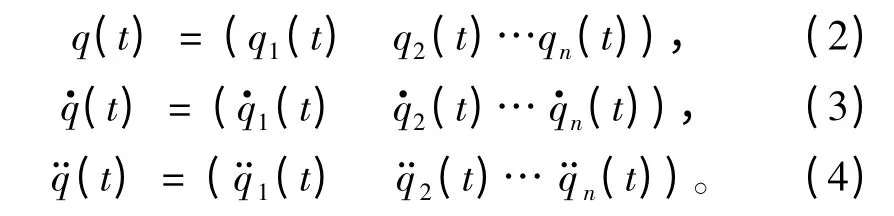
令:

则式(1)可表示为:

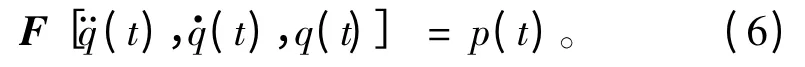
在Δt+t 时刻，振动系统传递函数为:

将式(6)和式(7)采用泰勒级数法计算化简得得:

状态方程中系数M，D 和K 与受力之间的关系如下:

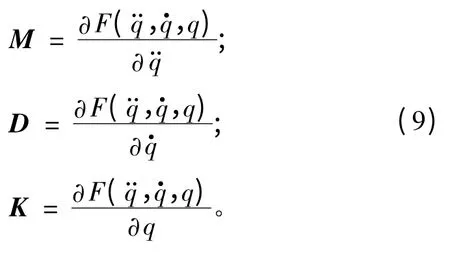
在求解上述方程时，首先用数值计算方法求解t 时刻和t + Δt 时刻的系统状态，当系统t 时刻的状态已知，则可确定微分方程的系数M，D 和K。类似地可求出下一时间段的系统状态参数，即可计算出t+Δt 时刻的系统状态，如此往复计算过程可得到轴系振动系统在某一段时间内的系统振动状态。

2 轴系仿真模型的建立

本文选用三维建模软件Solidworks 建立轴系的三维模型，其主要尺寸如表1 所示，所建立的三维模型如图2 所示。模型主要包括旋转副、多轴段和必要的联轴器等。在Solidworks 中将三维模型保存为ADAMS 能够识别的parasolid 格式文件。

表1 船舶推进轴系典型尺寸Tab.1 A typical size of ship propulsion shafting

图2 船舶推进轴系几何建模Fig.2 Ship propulsion shafting geometric modeling

在ADAMS 中多刚体模型的主要参数设置方法如下:

1)材料属性设置

本模型中旋转副、多轴段和必要的联轴器等均为钢材质，密度、弹性模量和泊松比按照钢材质的典型参数设置。

2)部件间运动约束设置

从Solidworks 导入到ADAMS 中的模型部件之间的关系的静态关系，且各部件的自由度均为6 自由度，处于无约束状态。而在船舶推进轴系工作时，轴系各部件之间均存在相对位移，因此，需要根据实际情况在各部件上施加特定运动约束。轴系部件的约束设置如下:轴承外圈与机架之间设置固定副、中间轴与对应的轴节间设定固定副，中间轴与轴承内圈之间设定旋转副，尾轴与机架之间设定固定副。

3)施加载荷

考虑到推进轴系的动力主要由发动机提供且假设忽略发动机因燃气压力改变造成的输出功率周期性变化，本文在轴系输入端施加扭矩，扭矩的大小取决于发动机功率的大小，其计算方法如式(10)所示:

即:

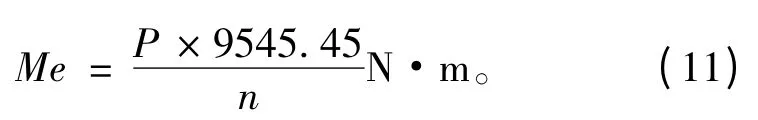
式中:P 为发动机功率;Me为发动机扭矩;n 为发动机转速。当P=4 440 kW 时，Me=2.45×104N·m。

3 基于ADAMS 的轴系扭振特性及动力学仿真

3.1 模态分析

推进轴系的模态是指轴系的固有振动特性，包括频率、阻尼大小和振型等信息。本文选用Ansys对轴系模型进行20 阶自由模态分析，前10 阶固有频率如表2 所示。

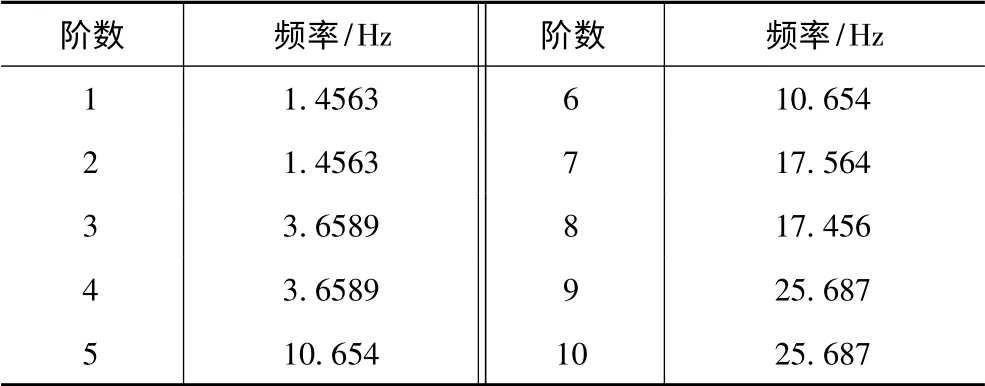
表2 推进轴系固有频率Tab.2 Propulsion shafting natural frequency

由表2 可看出，推进轴系的固有频率多数成对出现，该结果符合轴的对称特性，表明该模态分析结果的合理性。

3.2 推进轴系动力学特性计算

使用ADAMS - solver 求解器模块和ADAMS -postprocessor 模块对上述多体模型进行仿真分析，仿真轴系的角加速度曲线如图3 所示。该轴系是在稳定转速下工作，角速度为1 040°/s，角速度波动接近0。由图3 可知，轴系的角加速度呈类周期性波动，大致趋势是先激增后缓慢减小并接近零值，在数值上角加速度为0.001 5°/s2。该结果间接表明本文所建立的多刚体运动学特性的合理性。

图3 仿真轴系的角加速度曲线图Fig.3 The simulation of shafting angular acceleration curve

图4 为尾轴动力学特性的仿真结果。中间轴与尾轴管的动力学曲线大致相似，均在轴系摩擦系数变化是发生改变，该现象产生的主要原因是尾轴的支撑力能够具有使轴系稳定振动状态的效果。

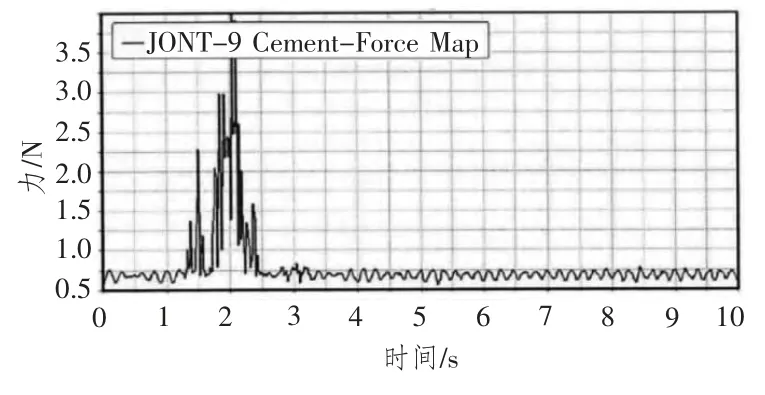
图4 尾轴受力曲线Fig.4 The stern shaft stress curve

3.3 推进轴系扭转特性分析

推进轴系扭转特性分析的本质是已知振动系统的激励和响应求系统的振动特性，即属于震源预测问题。本文首先采用ADAMS 的Vibration 模块对轴系进行一次静态平衡分析，通过线性分析获得轴系的固有频率和振型。图5 所示为推进轴系扭转振动特性的频率响应曲线，图中所示轴系振动响应的峰值分别为4，14，26，32，34，40，60，92，175，4，280 Hz，其中低频与ADAMS 线性分析的固有频率结果相接近。该仿真结果从侧面反映了本文所计算得到的系统固有频率的可行度。

图5 推进轴系扭转变形的频响特性Fig.5 The frequency response characteristics of propulsion shafting torsional deformation

为获得轴系实际振幅及力矩变化曲线，本文进行了推进轴系的强迫振动计算。在计算过程中，通过测量扭转角的大小来表征轴系的振动幅值，图6 ～图8 分别为轴系在额定稳定工况、轴承摩擦严重工况和螺旋桨受冲击工况下的轴系振动幅值曲线图。

图6 正常条件下轴系振动幅值曲线图Fig.6 Under normal conditions of shafting vibration amplitude curves

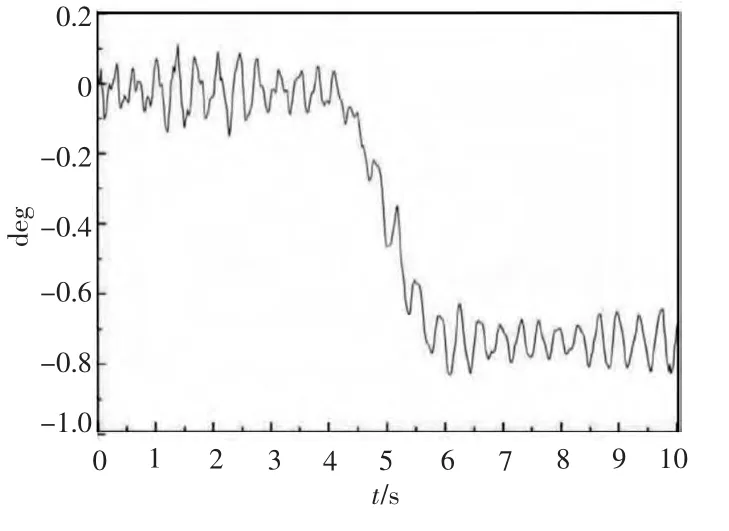
图7 轴承摩擦严重工况下轴系振动幅值曲线图Fig.7 Bearing friction shafting vibration amplitude curves of serious condition

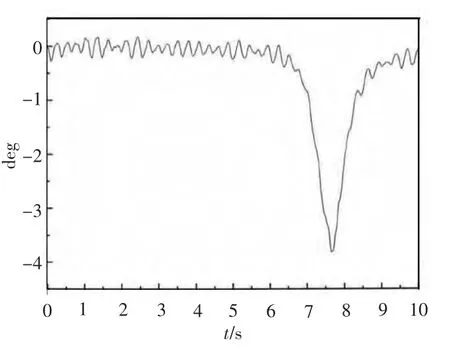
图8 轴系终端受外力冲击时轴系振动幅值曲线图Fig.8 Shafting terminal is impacted by the external force when the shafting vibration amplitude curves

由图6 可看出，推进轴系在施加负载后轴系的扭转角呈周期性变化趋势，振幅较大且峰值可达0.65°;由图7 可看出，在轴承磨损的条件下，因摩擦力不断增加导致扭转角逐渐升高，达到稳定后在0.9°附近波动;由图8 可以看出，当轴系终端螺旋桨受到因海洋风浪突变环境因此的随机冲击时，轴系的扭转角也将产生较大幅值的波动，图中最大扭转角达到了4.5°左右。

4 结 语

本文在深入分析推进轴系扭振特性及其动力学理论的基础上，将在Solidworks 中建立的船舶推进轴系三维实体模型导入ADAMS 中形成轴系的多体动力学模型并对该模型进行了自由模态分析、动力学特性分析和轴系在不同工况下的扭振特性分析。为获得轴系实际振幅及力矩变化曲线，进行了推进轴系的强迫振动计算。在计算过程中，通过测量扭转角的大小来标准表征轴系的振动幅值。推进轴系在施加负载后轴系的扭转角呈周期性变化趋势，振幅较大且峰值可达0.65°。在旋转副失效的条件下，扭转角在0.9°附近波动。当轴系终端螺旋桨受到冲击时，轴系的扭转角也将产生较大幅值的波动，最大扭转角达到了4.5°左右。

［1］张居凤，汪玉，方志刚，等.舰船动力系统配置方案可行性分析方法［J］.舰船科学技术，2011，33(9):60 -63.ZHANG Ju-feng，WANG Yu，FANG Zhi-gang，et al.Analysis on feasible configuration alternatives of ship power system［J］.Ship Science and Technology，2011，33(9):60-63.

［2］赵同宾，邱爱华，祁亮，等.海洋科学考察船动力系统发展现状及趋势［J］.舰船科学技术，2014，36(增刊1):52-55.ZHANG Tong-bin，QIU Ai-hua，QI Liang，et al.Developing status and trend of ocean research ship power plant system［J］.Ship Science and Technology，2014，36(S1):52 -55.

［3］HYUNG Han. Analysis of fatigue failure on the keyway of the reduction gearinput shaft connecting a diesel engine caused by torsional vibration［J］. Engineering Failure Analysis，2014，44:285 -298.

［4］高文志，刘建国，郝志勇. 基于二次型全局最优控制算法的汽轮发电机组轴系扭振主动控制模拟［J］.机械工程学报，2006，42(6):97 -105.GAO Wen-zhi，LIU Jian-guo，HAO Zhi-yong.Active control simulation of torsional vibration for turbine-generator shaft system based on globally optimal control algorithms of quadratic regulator［J］. Chinese Journal of Mechanical Engineering，2006，42(6):97 -105.

［5］吴炜，曹宏涛，陈汝刚，等.船舶推进轴段蠕变减缓应对措施研究［J］.舰船科学技术，2009，31(7):48 -50.WU Wei，CAO Hong-tao，CHEN Ru-gang，et al.Studies on measure for decreasing the creep of the vessel′s propulsion shaft segment［J］. Ship Science and Technology，2009，31(7):48 -50.

［6］王伟，余震，邱云明，等. 船艇轴系扭振状态测试与分析［J］.舰船科学技术，2009，31(6):51 -54.WANG Wei，YU Zhen，QIU Yun-ming，et al. The measurement and analysis on ship shaft′s torsional vibration status［J］.Ship Science and Technology，2009，31(6):51 -54.

［7］朱俊飞，周瑞平，胡义，等. 带齿轮副船舶推进轴系动态响应仿真研究［J］.振动与冲击，2013，32(9):100 -104.ZHU Jun-fei，ZHOU Duan-ping，HU Yi，et al. Dynamic response simulation on marine propulsion shaft with gear pair［J］.Journal of Vibration and Shock，2013，32(9):100-104.

［8］韩东江，杨金福，耿加民，等. 高速永磁电动机气体轴承-转子系统振动特性［J］.航空动力学报，2013，28(8):1791 -1796.HAN Dong-jiang，YANG Jin-fu，Geng Jia-min，et al.Vibration characteristics of gas bearing-rotor system of highspeed permanent magnet machine［J］.Journal of Aerospace Power，2013，28(8):1791 -1796.

［9］龚仁吉，肖玲斐.航空发动机变参数模型与滑模控制研究［J］.伺服控制，2014(2):35 -38.

［10］WU J J. Torsional vibration analysis of a damped shafting system using tapered shaft element［J］. Journal of Sound and Vibration，2007(5):946 -954.