基于Mamdani型直觉模糊推理的图像融合算法
2014-12-18孙祺,那彦,刘波
孙 祺,那 彦,刘 波
(西安电子科技大学电子工程学院,陕西西安 710071)
图像融合是将不同传感器对同一场景的成像融合成一幅新的图像,以获得更多信息的过程。融合后的图像可信度更高、模糊较少,为计算机视觉检测、分类、识别等提供必要的准备,具有重要的意义[1]。1986年K.T.Atanassov教授在模糊理论的基础上提出直觉模糊理论[2],创造性地引入了“非隶属度”这一参数,使直觉模糊集不仅可以描述对象“亦此亦彼”的模糊概念,还可以描述其“非此非彼”的中立概念,具有良好的应用前景。
最早将模糊理论引入图像融合的是加拿大的A Nejatali和 IR Ciric[3],随着近年来的发展,基于模糊理论的图像融合算法得到了广泛的研究[4-5],也出现了少量基于直觉模糊理论的图像融合算法[6]。但这些算法只引入了直觉模糊逻辑,算法复杂、不灵活,针对这些问题本文提出一种基于Mamdani型直觉模糊推理的图像融合算法,通过制定合理的融合规则确定直觉模糊推理系统,将待融合图像作为系统输入即可得到融合图像,操作简便、效果良好,通过改变推理规则可完成不同的融合目标。由于直觉模糊集较模糊集更加细腻地描述了客观事物的不确定性,因此基于直觉模糊集的推理系统较传统的模糊推理系统更具优势,推理结果也较好。
1 直觉模糊推理系统
1.1 直觉模糊集
直觉模糊子集A定义为[2]
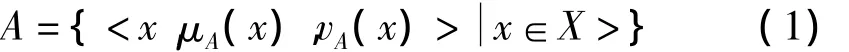
其中,μA(x)∶X→[0,1]和vA(x)∶X→[0,1]分别代表A的隶属度函数μA(x)和非隶属度函数vA(x),且对于A上所有x∈X,0≤μA(x)+vA(x)≤1成立。X上的全体直觉模糊子集记作IF(X)。在不引起混淆的情况下,直觉模糊子集也称为直觉模糊集。
由定义可知,论域X上的直觉模糊子集A由隶属度函数μA(x)和非隶属度函数vA(x)来表征,μA(x)的大小反映了x对于直觉模糊子集A的隶属程度,而vA(x)反映了x对于直觉模糊子集A的非隶属度程度,二者之和<1。
1.2 直觉模糊推理系统
直觉模糊推理本质上是一个从输入到输出的映射,并且该映射可以是复杂的非线性映射。实现这一映射的主要机制是一组被称为规则的“if-then”语句,也称为“if-then”规则库,它是整个推理系统的核心。一个简单的“if-then”规则具有如下形式[7]

它表示“如果输入(x)是A,那么输出(y)是B”,它是一种用自然语言描述的输入和输出之间的映射关系。其中A和B是自然语言描述的概念,具有一定的模糊性,在推理时用论域X和论域Y上的直觉模糊集来表示,也可以认为A和B就是直觉模糊集。例如图像灰度“暗”、“正常”、“亮”这3个模糊概念就可分别用3个直觉模糊集表示。“if-then”规则描述的输入输出间的关系,称为直觉模糊蕴含关系,记为A→B,用直觉模糊蕴含矩阵R(A→B)(x,y)或R表示,使用直觉模糊蕴含算子计算[8]。
直觉模糊推理的基本原理是已知输入输出间的映射关系(“if-then”规则)和现在的输入“A”,然后计算直觉模糊蕴含矩阵R,再将R与A'做合成运算,即可得到输入A'对应的输出B'。其计算公式表示为

其中,A、A'、B和B'均为由直觉模糊集表示的模糊概念;“·”为合成算子。A'和A虽不同,但却并非完全不同,其之间也较为相似,且系统输出的B'和B也相似,因此直觉模糊推理是一种近似推理。
不难发现,以上介绍的直觉模糊推理其输入输出均为直觉模糊集表示的模糊概念,当系统的输入输出需要为精确值时,就要对系统的精确输入进行直觉模糊化,系统的模糊输出进行解模糊运算。这种输入输出均为精确值的推理系统即为Mamdani型推理系统。
2 基于Mamdani型模糊推理图像融合算法
在图像融合中,图像的研究对象、背景、轮廓、边缘等都是一些模糊信息,对于一个像素点,很难对其进行准确的分类。对于图像中这种不确定信息,直觉模糊集合提供了较好的解决方法,它为每一个像素点提供一对隶属度、非隶属度值来描述其和某一个集合的关系,这样每个像素点可以同时属于多个不同的集合,但它们对集合的隶属程度不同。直觉模糊推理系统针对不同的直觉模糊集合提供不同的融合规则,并根据推理算子和决策算子给出最终的融合结果,使得融合图像更加符合人类的视觉感知,获得更好的融合效果。
2.1 直觉模糊规则库的设计
本文针对CT、MRI医学灰度图像进行融合,推理系统输出为output,即融合图像。输入输出图像像素点灰度值的取值范围为(0~255),按照灰度值由小到大的顺序将其划分为3个灰度级别:暗(Dark),正常(Normal),亮(Bright)。由于CT、MRI图像的背景灰度值较小,而表示信息的部分灰度值相对较大,为了获得更多的图像信息,本文设定“灰度级别取大”为融合目标(灰度级别Dark<Normal<Bright),并根据融合目标设计推理规则库如下:
规则 1 If CT is Bright or MRI is Bright,then output is Bright;
规则 2 If CT is Normal and MRI is Normal,then output is Normal;
规则 3 If CT is Normal and MRI is Dark,then output is Normal;
规则 4 If CT is Dark and MRI is Normal,then output is Normal;
规则 5 If CT is Dark and MRI is Dark,then output is Dark;
将自然语言描述的输入输出映射关系用直觉模糊蕴含矩组[R1,R2,…,R5]阵表示,其计算步骤如下:
第1步 确定输入输出直觉模糊集。本文直觉模糊集的隶属度函数μ(x)、非隶属度函数v(x)均取三角型函数,即

对于输入图像,3个灰度级别分别用论域X上的直觉模糊集D、N、B表示,其隶属度函数对应参数 a、b、c的值分别为[-0.4 0 0.4]、[0.2 0.5 0.8]和[0.6 1 1.4];非隶属度函数对应参数a、b、c的值分别为[-0.4 0 0.4]、[0.1 0.5 1]和[0.6 1 1.4]。对于输出图像,3个灰度级别分别用论域Y上的直觉模糊集D'、N'、B'表示,其隶属度函数对应参数a、b、c的值分别为[-0.3 0 0.3]、[0.3 0.5 0.7]、[0.7 1 1.3];非隶属度函数对应参数同隶属度函数。
第2步 规则前件合成运算。本文的推理系统有两个输入,在推理规则中使用连接词“or”或“and”进行连接,逻辑上分别表示两个输入之间“或”和“与”的关系,在推理时为直觉模糊集合间的一种运算,可将两个输入合并为一个输入。设规则i的两个输入合成直觉模糊集Mi,则Mi为

其中,直觉模糊集Ii1=(〈μi1(x),vi1(x)〉x∈X)为规则i第一个输入对应的直觉模糊集,Ii2=(〈μi2(x),vi2(x)〉x∈X)为规则i第二个输入对应的直觉模糊集。例如对应规则3,I31=N,I32=D。
第3步 计算直觉模糊蕴含矩阵组。本文选择Mamdani型直觉模糊蕴含算子,则规则i的Mamdani型直觉模糊蕴含矩阵Ri为
Ri(x,y)=(μMi(x)∧μi(y),vMi(x)∨vi(y))(7)其中,“∧”表示取小,“∨”表示取大;Oi=(〈μi(y),vi(y)〉y∈Y)为规则i输出部分对应的直觉模糊集。例如规则 1,O1=B'。
2.2 图像融合算法的实现
基于Mamdani型直觉模糊推理的图像融合算法流程如图1所示,将输入的待融合图像中的每个像素点(i,j)作为系统输入,其融合方法步骤为:

图1 基于Mamdani型系统的医学图像融合算法流程图
第1步 根据上一节的步骤确定“if-then”融合规则并计算直觉模糊蕴含矩阵组。
第2步 输入CT和MRI图像,进行预处理。
第3步 直觉模糊化,本文采用单点直觉模糊化的方法,灰度值为x0的像素点可直觉模糊化为

其中,L取值为直觉模糊集D、N、B。
第4步 输入合成运算,将CT、MRI位于(i,j)处的像素对应的直觉模糊集做合成运算,得到一个直觉模糊集作为推理系统的输入,为下一步与蕴含矩阵组的合成运算做准备。
第5步 将第4步得到的直觉模糊集与表示规则库的模糊蕴含矩阵组做合成运算,根据式(3)进行推理,得到每条规则的推理结果。本文采用最大-最小合成算法,设已知输入直觉模糊集合A'和直觉模糊蕴含矩阵R,推理输出为直觉模糊集,则的隶属度、非隶属度函数为

第6步 综合第5步各条规则的推理结果,得到一个直觉模糊集作为最终输出。
第7步 将第6步得到的融合图像中每个像素点(i,j)对应的直觉模糊集进行解模糊计算,得到融合图像中每个像素点(i,j)的灰度值,并最后合成融合图像。
3 仿真实验及分析
使用Matlab2010对本文提出的算法进行仿真实验,同时对文献[6]中的直觉模糊推理融合算法以及基于Mamdani型模糊推理系统的融合算法进行仿真实验并作为对比方法。待融合医学图像如图2所示,3种算法的融合结果如图3所示。使用Matlab计算各融合图像的标准差、均方差、峰值信噪比和信息熵等,作为客观分析融合图像质量及评价融合算法的重要依据。根据文献[9],融合图像的标准差越大,图像像素点的灰度相对于其平均值越离散;均方差越小,融合图像与原图像越接近,融合效果越好;峰值信噪比越大,融合图像的失真越小;信息熵越大,融合图像所包含的信息越丰富。3种算法融合图像的评价参数如表1所示。

图2 待融合CT和MRI图像

图3 融合结果图像

表1 融合结果参数对比
观察图3中的融合图像可以看到,3种方法都取得了良好的融合效果,但M型直觉模糊推理算法优于另外两种算法,其融合图片能够看到更多的细节信息,对比度明显,边缘轮廓清晰。
分析表1中的数据,可知本文提出的算法,除标准差外,融合图像的其他评价参数较另外两种方法均有所提高,说明由本文算法得到的融合图像效果较好,包含了更多的图像信息。由本文算法得到的图像优于基于M模糊推理算法得到的图像,说明直觉模糊集在推理系统中发挥了更大的作用,在处理图像不确定信息时具有更多的优势。基于推理系统的两种融合算法,其融合图像的标准差都有所下降,这是因为推理系统在处理图像的不确定信息时会同时激活每条规则,对同一个输入,对应每条规则都有一个输出,而系统的最终输出是各规则输出的综合。这一过程类似于对输入进行加权平均,必然会降低图像的灰度离散程度。因此,如何减轻推理系统这一缺点对融合图像造成的影响也是未来的研究目标。
4 结束语
本文提出了基于Mamdain型直觉模糊推理的图像融合算法,数学建模符合人类思维过程,只需根据融合规则并选择合适的输入输出隶属度、非隶属度函数建立推理系统,将待融合图像输入系统即可得到融合图像。实验结果证明了该算法的可行性及有效性,验证了直觉模糊集在描述事物本质方面的优势,较好地将直觉模糊理论用于图像融合领域。
[1]郭雷,李晖晖,鲍永生.图像融合[M].北京:电子工业出版社,2008.
[2]KRASIMIR T A.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986(20):87 -96.
[3]NEJATALI A,CIRICI R.Novel image fusion methodology using fuzzy set theory[J].Optical Engineering,1998,37(2):485-491.
[4]NA Yan,LU Hongmin,ZHANG Ying.Content analysis based medical images fusion fuzzy inference[C].The 5thInternational Conference on Fifth International Conference on Fuzzy Systems and Knowledge Discovery,2003:37 -41.
[5]TANGJionghua,WANGSuhuan,ZHANGJingzhou,et al.Fusion algorithm of medical images based on fuzzy logic[C].2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery,2010:546 -550.
[6]赵梦旸,那彦,李思彤.基于直觉模糊推理的医学图像融合方法研究[J].电子科技,2012,25(3):48 -50,54.
[7]吴晓莉,林哲辉.Matlab辅助模糊系统设计[M].西安:西安电子科技大学出版社,2002.
[8]林琳.直觉模糊推理[D].大连:辽宁师范大学,2003.
[9]那彦,杨万海,吴艳.图像模糊信息融合算法的性能评价[J].西北师范大学学报:自然科学版,2002,38(2):44-46.
