激光激发板状分层材料的超声波场模拟

许伯强，李俊敏，徐桂东，张景秀

(1.江苏大学理学院，江苏镇江 212013;2.江苏大学机械工程学院，江苏镇江 212013)

近年导波传播特性的研究已由单层材料发展到多层模型，用于指导材料的无损评价和检测。波在不同材料中的传播特性由界面的边界条件决定，波在媒质中的传播受层间界面的限制而产生不同形式的反射或散射。因此，对无限大或半无限大基底，以及有限边界对表面波传播的影响进行分析是必要的。而波在不同材料中的传播特性由界面的边界条件决定。Brekhovskikh(1980)，Ewing(1957)及 Pace(1983)都曾发表文章来全面讨论这些类型的边界条件［1］。在无限大固体中，可能存在波的模式有P波和S波两种类型。当这些波到达边界时，会在局部有更多的边界效应产生。在多层介质的情况下会由于层间反射而造成色散。已有的许多研究通过理论和实验的方法获得了导波传播的色散曲线，层状波导的色散方程大多采用传递矩阵法或全局矩阵法建立。而本研究中的动态刚度矩阵对双层结构中的超声研究沿袭了传递矩阵的思想。因此，文中主要采用谱有限元法构造动态刚度矩阵对薄膜－基底层状材料中的传播特性进行研究，并初步对二维层状结构的应力产生的超声波场进行了模拟分析。

本研究主要是将谱方法与传递矩阵方法相结合，结合了谱方法与有限元法各自的优点，扩展 Doyle(1988)的一维波导分析，在二维模型中，将刚度建立在频率/波数域。时域偏微分波动方程变换到频域常微分方程的同时也将计算从时域瞬态求解转换到频域准静态计算，最后基于Matlab程序求解相应常微分方程得到所求的解。

1 波谱分析

1.1 控制方程

位移的控制方程是用来简化弹性理论下系统的未知位移变量在波场中的公式，总结为Navier公式［2－4］

由亥姆霍兹分解得到关于势函数的偏微分波动方程标量势Φ和矢量势H分别对应限制相速度Cp和Cs的P波和SV波，将y方向退化，只考虑xoz截面的两个传播方向。将控制方程变换后得到频率/波数域的求解表达式。序列的N次叠加和表示表达式中有N个频率分量。若给定的某一序列点的波数η就可给出波随时间的变化。当η为零时，取不同频率的叠加即可得到平面波的变化趋势。

1.2 谱单元分析

文中讨论了两种类型的谱单元，单节点的截断单元和双节点的层单元。截断单元模拟的是半无限大板材，而双节点单元则是有限大模型两端均有边界的情况。

图1 两种类型单元模型几何示意图

1.2.1 1－节点单元

如图1(a)所示的单元只有单一边界条件，位移u和v的谱展开表达式为

此式中既包括对称模态也包括反对称模态，然而本研究的几何模型关于y轴对称，因此只包括对称部分。式(4)取节点1(z=0)时的值即为节点位移。

由柯西应力法则牵引力的边界受力表达式为

式(5)中，nx、ny分别表示关于下标方向垂直于表面的法向分量，在节点1取外法向分量可以得到牵引力与待定系数的关系式。μ是剪切模量，也就是得到单元刚度矩阵

1.2.2 2－节点单元

双节点单元的分析与单节点类似，其几何模型如图1(b)所示，势函数的表达式在该模型系统下修正为［5］

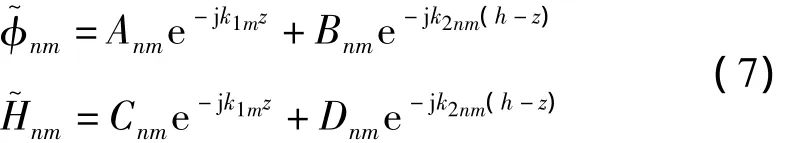
同理推导位移与待定系数［AnmBnmCnmDnm］T的关系，将z1=0，z2=h代入位移表达式，下标1、2分别用以区分层单元的上下表面。

通过应力或应变向量过渡得到牵引力向量与位移向量之间的关系

得到求解核心刚度矩阵即可分析给定材料矩阵元素随频率的变化关系，取极限是当η=0时的低频下谱单元平面波，如图6所示是在相应值时元素低频响应。由表达式可知k12、k14为恒定零值。而其他各元素分别在低频区域呈递减走势，其中k11、k13呈现的是类似于棒的u位移特性。k22、k24则是与v位移相关联，类似于梁的剪切特性。随着水平方向波数η的增大，将会有更多的元素在低频区域趋向于零。

2 数值模拟

2.1 几何模型与边界条件

脉冲激光作用可产生谐波，其等效力源的表达式如式(9)所示，其时域与频域分布如图2所示［6］

其中，σ=1.2表示激光脉冲宽度的控制参量;t0=5μs表示脉冲延迟时间;fc=0.5 MHz。对f(t)进行傅里叶变换得到其频谱。

图2 上表面荷载时域波形及频谱

图3 双层板几何模型示意图

表1 材料参数

基于上述理论，建立频域谱有限元双层模型，上层材料为铝，下层材料为钢。

2.2 结果与讨论

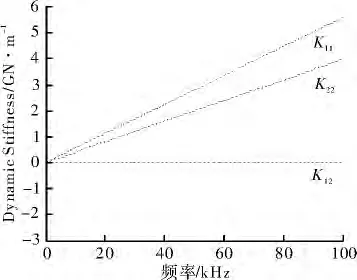
图4 截断层的动态刚度元素随频率的变化(η=0)

图5 截断层的动态刚度元素随频率的变化(η=99)

图6和图7为η=0时刚度随频率的变化图，对比可看出双节点单元平面波的传播会在到达第二个节点处时改变耦合关系，反向也如此。这是因为当η增大时，x方向的指数函数衰减更剧烈。图6与图7分别为低频及全频率范围的刚度矩阵变化趋势。在频率增大区域刚度具有共振特性，与图5所示一致。对波数作相同的定量分析结果也如此。

图6 平面波在双节点单元传播的刚度矩阵低频特性(η=0)

如图8所示，随着超声导波的传播距离增加，材料中超声导波的振幅基本没有变化。激光作用在材料表面依次激发 P波、S波以及紧跟其后的 Rayleigh波(R)。能明显地分辨出波形中不同模态超声导波的特征。图8中可清晰地看出反射波中相继出现的两种不同模态的超声导波，不同模态的超声导波传播速度均相等，标注为RR和RS。与之相比，图9所示为上下层分界面处取点，其峰值与图8相反，SP波模式先到达交界面处引起小的扰动，随后峰值到达引起大的扰动。

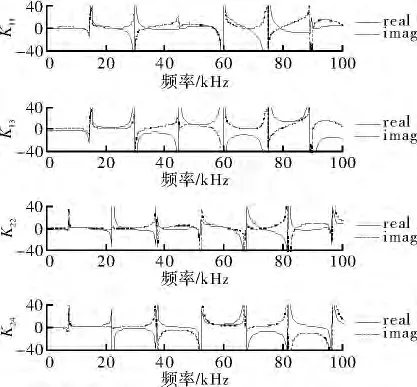
图7 平面波在双节点单元传播的刚度矩阵全频率范围内特性(η=0)

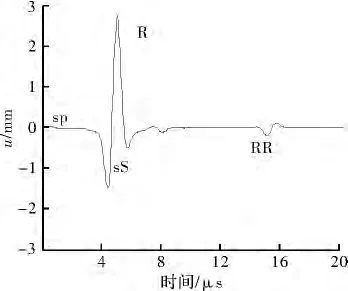
图8 表面源点30 mm处位移场

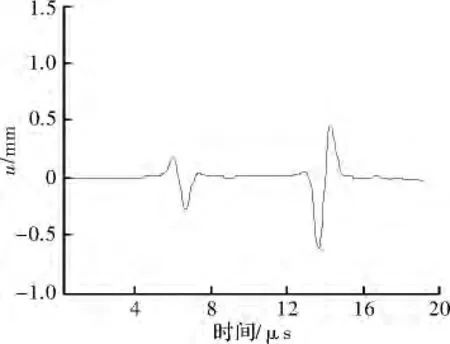
图9 交界面水平30 mm处的位移

图10与图11分别描述表面和交界面上取距离源点0.2 m处位移场的时间变化。表面距源0.2 m处首先在激发中心5μs处达到峰值随后在每隔35μs有一个反射峰，由超声波在铝材料中的传播速度为6 200 m/s，每次经过底面反射有一部分波能量被截止单元泄露导致每一次到达上表面检测点都会衰减。图11与图10相比，峰值延迟到达，共同表征波在上层单元往返衰减。

图10 表面距源点0.2 m处位移场的时间变化

图11 表面源点0.2 m处位移场的时间变化

计算过程采用的时间采样频率为2 048/1 000μs，空间采样频率为1 024/1 m，计算时间为(Elapsed time)为 247.188 896 s。

3 结束语

结果表明，该种将谱方法与有限元结合的矩阵构造方法推导过程简洁，可将动态刚度矩阵的元素随频率的变化更直观地表达出来，对各向同性板状材料的模拟过程简洁明了，大幅节约了计算时间及内存，并可有效分析平面应力波在层状介质中的传播。同时，这一过程将整个层作为一个单元，可有效降低整个系统的尺寸。此外，还可考虑从推导过程出发，改变本构方程向横观各向同性材料的扩展，亦可考虑加入缺陷作进一步研究。

［1］BREKHOVSKIKH L M.Waves in Layered Media［M］.2nd ed.Russia:Academic Press，1980.

［2］SHEN Zhonghua，XU Baiqiang，NI Xiaowu，et al.Numerical simulation of pulsed laser induced ultrasound in monolayer and double layer materials［J］.Chinese Journal of Lasers，2004，31(10):1275 －1280.

［3］RIZZI SA.A spectral analysis approach to wave propagation in layered solids［D］.USA:Purdue University，1989.

［4］ZIENKIEWICZ O C，TALOR R L.The finite element method for solid and structural mechanics［M］.Oxford:Elsevior Butterworth － Heinemann，2005.

［5］DOYLE R，DOYLE JF.A spectral element approach to wave motion in layered solids［J］.Journal of Vibration and Acoustics，1992(6):569 －577.

［6］孙宏祥，许伯强，徐晨光，等.横观各向同性材料中激光超声谱有限元法数值模拟［J］.光子学报，2009(5):1041－1046.

［7］YANG T Y.Finite element structural analysis［M］.MC USA:Prentice － Hall，1986.

［8］曹飞，李丽国，余学才.激光超声无损检测系统设计［J］.电子科技，2006(11):64－67.