基于遗传神经网络的AOA跟踪算法

谢 川，毛永毅

(1.西安邮电大学通信与信息工程学院，陕西西安 710061;2.西安邮电大学研究生学院，陕西西安 710061)

目前，无线定位中常用的方法有基于到达时间(Time of Arrival，TOA)定位［1］、基于到达时间差(Time Difference of Arrival，TDOA)定位［2］和基于到达角度(Angel of Arrival，AOA)定位［3－4］。随着智能天线阵列的广泛应用，使得通过基站来准确有效地测量移动台的AOA值变成可能。基于到达角度的无线定位方法无需移动台与基站之间严格同步，具有广阔的应用前景［5］。

由于神经网络具有较快的学习特性和任意非线性映射逼近的能力，通常将其用于消除无线传播中的非视距(Non Line of Sight，NLOS)误差。例如文献［6］中给出了一种基于径向基函数神经网络的定位算法，文献［7］中给出了一种基于后向传播(Back Propagation，BP)神经网络的室内定位模型。但神经网络仍存在较大的缺陷，对于如何使用其它智能算法来优化神经网络并结合应用于移动台定位的文献资料较少。在现实生活中，移动台的位置是处于连续变化的状态，而现有算法研究大多针对移动台的静态定位，对移动台实施动态跟踪的研究则较少涉及。

为了对移动台实现有效的动态跟踪并提高定位精度，本文使用遗传算法来优化BP神经网络的初始权值，使用优化后的GA－BP(Genetic Algorithm－Back Propagation，GA－BP)神经网络对非视距传播环境中的AOA(Angel of Arrival，AOA)测量值进行修正，再使用卡尔曼滤波器［8－9］配合相关检测距离门对移动台实施跟踪。最后对该方法的性能进行了仿真和评估分析。

1 基于BP神经网络的AOA值修正模型

BP网络具有强大的自适应和自学习能力，是目前使用最为广泛的神经网络模型之一。本文利用BP神经网络来对AOA测量值中的NLOS误差进行修正。图1为在NLOS环境下由7个基站提供AOA测量值的BP神经网络3层修正模型。

图1 BP神经网络3层修正模型

(1)将典型的7个相关基站所提供的7个AOA测量值作为输入向量，可表示为

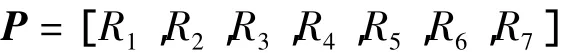
(2)隐含层传递函数采用Sigmoid型函数f1(x)=tan h(x)，输入为任意值，输出则在［－1，1］之间;其中隐含层神经元的个数根据经验选择为18。

(3)输出层传递函数采用Purelin型函数f2(x)=kx，输出向量为修正后的AOA值

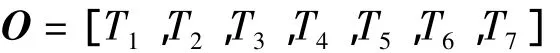
2 遗传算法优化BP神经网络的初始权值

由于BP神经网络的初始权值选择具有随机性，通常容易导致网络震荡并陷入局部最优，而遗传算法具有强大的全局搜索能力，使用遗传算法来优化BP神经网络的初始权值，可以有效避免陷入局部最优。

遗传算法优化BP神经网络初始权值的具体步骤如下:

步骤1 首先对输入种群N(神经网络的权值)进行初始化，采用实数编码方式对神经网络的权值进行编码，编码长度为S=S1×S2+S2×S3+S2+S3，其中S1表示BP神经网络输入层神经元数目，S2表示隐含层神经元数目，S3表示输出层神经元数目。

步骤2 定义适应度函数如下

其中，fi表示个体i的适应度;Vk表示学习样本;Wk表示目标样本。

步骤3 对种群中所有个体的适应度函数进行运算并排序，按照以下概率值对个体进行选择

将其中适应度最高的个体复制生成下一代，不进行交叉与变异过程。剩下的个体则采用轮盘赌法将适应度最低的两个个体淘汰。

步骤4 按照交叉率Pc对个体Ni和Ni+1进行单点交叉后产生新的个体N'i和N'i+1。

步骤5 按照变异率Pm对个体Nj进行均匀变异后产生新的个体N'j。

步骤6 将新个体插入到种群N中，并对新个体的适应度函数进行运算。

步骤7 若找到了满足预设要求的个体，算法结束，否则转到步骤3。

通过以上步骤达到所要求的性能指标后，对所得到的最优个体解码即可得到遗传优化后的网络连接权值，并将权值赋给BP神经网络作为初始权值，然后使用BP算法将网络训练到预设精度。

3 基于遗传神经网络的AOA定位算法

利用遗传算法优化初始权值后的GA－BP神经网络来训练AOA测量值，然后利用LS算法进行定位，这样能够有效提升系统的定位性能。具体定位步骤如下:

(1)首先在非视距传播环境下，测定L组AOA测量值作为测试样本，建立基于遗传算法优化初始权值的GA－BP神经网络模型，然后使用移动台中不含有非视距误差的AOA值作为训练样本对网络进行训练。

(2)使用训练好的遗传神经网络模型(GA－BP)对L组非视距传播环境下的AOA测量值进行修正。

(3)得到 L组修正后的 AOA测量值，采用 LS(Least Square，LS)算法对移动台进行位置估计。

4 基于卡尔曼滤波的跟踪算法

通过以上定位算法获得移动台的位置初始估计值后，再利用卡尔曼滤波器配合相关检测距离门来对移动台实施动态跟踪。

4.1 跟踪算法的实现

假设移动台的速度变化量与观测噪声相互独立，卡尔曼滤波跟踪算法的迭代过程如下

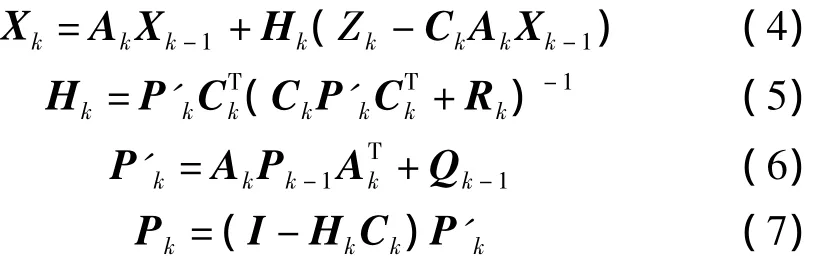
其中，X表示状态变量矢量矩阵;Zk为通过定位算法第K个测量值得到的移动台初始位置估计值，即观测值;P表示误差协方差矩阵;Qk表示移动台速度变化量的协方差矩阵;Rk表示观测误差(测量误差与NLOS误差之和)的协方差矩阵。

具体步骤如下:

(1)假设初始状态变量值X0=［z11z120 0］T;

(2)当K=2时，计算速度变化量的协方差矩阵Qk、观测误差的协方差矩阵Rk、误差协方差矩阵P0;

(3)将以上得到的各个值代入卡尔曼滤波跟踪算法的迭代式(4)～式(7)进行计算，得出新的移动台位置估计值。

(4)对比新得到的移动台位置估计值与预设的距离门限值G，若位置估计值大于距离门限值，则舍去该值，使用线性预测插值代替;若小于距离门限值，则保留该值。

4.2 距离门G的选取

考虑到移动台的动态随机性，算法选取移动台前3次移动距离的平均值作为距离门限值G。

距离门限值的计算公式如下

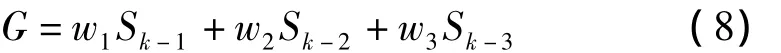
其中，Sk表示移动台第 K次移动的距离，

5 仿真与分析

为检验算法的可行性与实际性能，本文对该算法在NLOS环境下基于几何结构的单次反射(GBSB)统计信道模型进行了仿真分析。在仿真中，采用典型的由七个基站组成的蜂窝网络结构，服务基站BS1(0，0)位于小区中心，小区服务半径为3 000 m，移动台从坐标(200，200)处出发，沿与x坐标轴成45°角的方向匀速移动，移动速度为3 m/s。其中散射圆半径为200 m，AOA系统测量误差为独立同分布的均值为0，标准差为0.01 rad的高斯随机变量。设定遗传算法种群规模为50，最大遗传代数为10，交叉率 Pc为0.6，变异率Pm为0.001。

图2为本文定位算法和跟踪算法的仿真图，虚线代表移动台的实际移动轨迹，加号点迹代表本文算法(GA－BP)的定位轨迹，实线则代表本文算法(GABP)的跟踪轨迹。其中横坐标为观测的时间，纵坐标为移动点迹到服务基站BS1的距离。由仿真图可以看出，定位算法的点迹均处在移动台实际移动轨迹的两侧，但存在一些定位点迹与实际位置间的偏差较大，跟踪算法能够有效地舍弃掉那些与实际位置偏差较大的定位点迹，同时保留那些与实际位置偏差较小的定位点迹，从而实现了对移动台的有效跟踪。

图3和图4分别为本文算法与传统BP神经网络、LS算法在不同小区服务半径与散射圆半径下对跟踪结果均方误差(RMSE)值的比较情况。可以看出本文提出的基于遗传神经网络(GA－BP)算法的跟踪误差比传统BP神经网络、LS算法的跟踪误差更小，并且较为稳定。由此可知，本文算法的跟踪性能更优。

图2 定位与跟踪结果图

图3 不同小区半径的跟踪结果

图4 不同散射圆半径的跟踪结果

6 结束语

本文提出了一种在NLOS环境下基于遗传算法优化神经网络的AOA定位跟踪算法。本文将具有强大全局搜索能力的遗传算法和拥有较快学习特性的BP神经网络相结合，通过遗传算法对BP神经网络的初始权值进行优化，利用优化后的GA－BP神经网络对AOA测量值中的NLOS误差进行修正，采用LS算法进行位置估计，最后利用卡尔曼滤波器配合相关距离检测门对移动台进行跟踪。仿真结果表明，本文算法的动态跟踪性能优于传统BP神经网络与LS算法。

［1］陈健，卓永宁.一种基于TOA的定位优化算法［J］.无线电通信技术，2010，36(4):52 －54.

［2］YAMASAKI R，OGINO A，TAMAKI T，et al.TDOA location system for IEEE 802.11b WLAN ［C］.Losangelse:IEEE Wireless Communication and Networking Conference，IEEE，2005:2338－2343.

［3］BHARATH A，UPAMANYU M.Cooperative localization using angle of arrival measurements in non－line－of－sight environments ［C］.Sanfrancisco，California，USA:Mobile Communication Conference，2008:117 －122.

［4］兰云飞，王洪雁.在非视距传播环境下无线定位的AOA算法［J］.计算机仿真，2007，24(11):166 －168.

［5］毛永毅，李明远，张宝军.基于RBF神经网络的AOA定位算法［J］.计算机应用，2008，28(1):1－6.

［6］郭华，高幼林.基于支持向量机RBF神经网络的TDOA定位算法［J］.微电机，2011，44(4):106－109.

［7］李瑛，胡志刚.一种基于BP神经网络的室内定位模型［J］.计算机技术与自动化，2007，26(2):77 －80.

［8］段凯宇，张力军.基于到达角Kalman滤波的TDOAAOA定位算法［J］.电子与信息学报，2006，28(9):1710 －1713.

［9］李静，刘琚.用卡尔曼滤波器消除TOA中NLOS误差的三种方法［J］.通信学报，2005，26(1):131－141.