海原断裂带强震发生概率的评估方法
2014-12-17郭星潘华
郭 星 潘 华
1)中国北京100081中国地震局地球物理研究所
2)中国北京100082环境保护部核与辐射安全中心
引言
Reid(1910)在总结1906年加利福尼亚地震的震源机制时,根据对圣安德烈斯断层在地表的破裂面的观测,提出了著名的弹性回跳理论.根据这一理论,当应力累积量达到一个固定的上限值时则发生一次地震,随即断层源上的应力状态会下降到一个固定的极低水平,然后重新开始积累(冉洪流,何宏林,2006).
基于弹性回跳理论,断层源上强震的发生满足周期性模型(periodic model),而实际地震的发生并不满足周期性模型的理想化状态.为此,国外学者从时间不确定性和震级不确定性的角度,又分别提出了时间可预测模型(time-predictable model)和滑动可预测模型(slip-predictable model).
在Reid(1910)的周期性模型中,断层上对应于每次地震的摩擦强度、应力降和滑动量是恒定不变的,也就是说每次地震发生的时间和震级的大小是可以预测的.在时间可预测模型中,当应力累积量达到一个固定的上限值时则发生一次地震,而每次地震所释放的应力降、地震矩和滑动量均不同.假设应力积累速率恒定,且已知上一次地震的滑动量,则该模型可以预测下一次地震发生的时间.然而,未来将发生地震的强度和位移量却是未知的.此外,还有一种滑动可预测模型,该模型提出每次地震后应力状态会下降到一个固定的下限,而每次发生地震破裂时的上限应力状态却是变化的,地震破裂的重复周期也是变化的.只要给定一个不变的应力累积速率和距离上一次地震发生的时间,潜在地震的滑动量和震级的大小是可预测的;但由于没有固定的上限应力状态,下一次地震的发生时间是不可预测的(Shimazaki,Nakata,1980).
之后Aki(1984)以及Schwartz和Coppersmith(1984)以弹性回跳理论为基本的物理假定,提出了特征地震(characteristic earthquake)的概念.特征地震是指某些断层在长期活动过程中,重复发生的多次大地震往往表现出相似的破裂尺度、位错分布和震级大小.利用特征地震模型来研究大地震的活动性需要首先明确研究区域内的每个特征断层源,即有明确分段的断裂.每个分段断层源既可以发生单段破裂,也可以与相邻的几个分段断层源发生联合破裂(Abrahamson,2006).
特征地震模型是建立在周期性模型的基础上的,但实际上特征地震震级的大小存在不确定性,地震的发生也不是周期性的,而是具有一定随机扰动的准周期模型.此外,时间可预测模型和滑动可预测模型中选取的震源包括多种不同级别的破裂源,震级的分布范围也较大,远超过特征地震的震级不确定性范围.为此,Ellsworth等(1999)和Matthews等(2002)在周期性模型的基础上又提出了BPT(Brownian passage-time)模型.该模型假定断层源上的应力(或地震矩)加载过程包括一种稳定的自然加载和一种由各种随机因素所造成的布朗扰动,地震事件的复发间隔则服从BPT分布.然而,周期性模型的基本假设是大震发生时的上限应力状态和大震发生后的下限应力状态都是固定不变的,也就是说断层上每次地震的震级大小是一样的,这与实际不符合.BPT模型将加载过程中临界状态的不确定性放到了加载过程的不确定性之中,这也导致了震级不确定性信息的缺失.此外,BPT模型没有考虑时间与震级的相关性,而对于一个特征断层源来说,根据前人给出的各种震级-发震面积和震级-发震长度的经验关系式(Wells,Coppersmith,1994;Hanks,Bakun,2002;Working Group on California Earthquake Probabilities,2003;Leonard,2010),给定分段断层源上特征地震震级的不确定性上限和下限最大可相差1.0.因此,强震发生概率的计算过程中,能否同时给出明确的震级分布,对地震危险性分析结果的影响很大.
本文针对具有明确分段的特征断层源,从震级的不确定性出发,在弹性回跳理论的基础上提出一种随机特征滑动模型(stochastic characteristic-slip model).该模型假定分段断层源上发生强震的震级随机性满足特征地震模型,而大地震发生后断层源上的应力状态则下降到一个固定的下限.根据这种假设,对于特征断层源,未来一段时期内大地震的发生概率和震级的大小均与上一次大地震的发生时间有关.
本文选取分段较明确的海原断裂带为研究对象,利用海原断裂带上已取得的古地震和历史地震资料,并考虑到不同破裂尺度(单段破裂和全段破裂),采用随机特征滑动模型计算得到未来100年海原断裂带上强震发生的可能性及其震级分布.由于不同破裂源上的地震矩累积率的计算存在较大的不确定性,特别是次级破裂源上的地震矩累积率很难确定,本文提出利用蒙特卡罗方法估计不同尺度破裂源上的最大可能年平均地震矩累积率.
1 随机特征滑动模型
在随机特征滑动模型中,地震破裂时的临界应力状态的不确定性由断层源或分段断层源上震级的随机性决定,而这种震级的随机性则符合特征地震模型.特征地震发生以后,断层源上的应力状态则会下降到一个固定的极低水平,然后重新开始积累.
随机特征滑动模型不仅限于应力作为地震的状态物理量,也可以是地震矩或能量.由于地震矩与震级之间比较方便转换,本文选择地震矩作为模型的状态参数.
1.1 强震发生概率密度分布函数的计算
特征地震模型一般假定断层源上震级分布符合截断正态分布(Youngs,Coppersmith,1985),这种分布与震级-面积或震级-长度经验关系式中的随机变化一致.这种截断阻止了严重偏离研究区域内的“合理性”震级的极端地震事件的出现 (Working Group on California Earthquake Probabilities,2003).这种正态分布的概率密度函数的表达式为

式中,f(M)为破裂源上特征地震长期的震级分布,¯Mchar为破裂源上的平均特征震级,σM为表征破裂源上震级不确定性的标准差(Working Group on California Earthquake Probabilities,2003).
本文采用矩震级MW作为震级标度,震级为MW的地震所释放的地震矩M0由Hanks和Kanamori(1979)给出的矩震级-地震矩的经验关系式计算得到,即

式中地震矩M0的单位为N·m.若已知将要发生的潜在地震的震级MW和断层源上的年平均地震矩累积率˙M0,则可以计算出该潜在地震与前一次地震之间的复发间隔T为

根据式(2)和(3)可知复发间隔T与震级MW之间存在线性关系,则可计算得到T符合截断对数正态分布为

其中,T的取值范围为101.5(¯Mchar-2σM)+16.1/˙M0-101.5(¯Mchar+2σM)+16.1/˙M0.μlnT和σlnT的表达式分别为

1.2 条件概率的估计
若已知强震发生的概率密度分布函数f(T)和前一次特征地震的离逝时间Te,就可以计算特征断层源上未来一段时间ΔTe内强震发生的条件概率(Wesnousky,1986)为

式中ΔTe一般取50年或100年.
2 海原断裂带及其破裂源
海原断裂带上曾发生过1920年海原8.5级大地震,造成了约22万人死亡,并形成了长约230km的地表破裂带.海源断裂带的晚第四纪活动以左旋走滑为主要特征,走滑位移量可达10—15km(张培震等,2003).近20余年来,研究人员在海原断裂带上获得了大量的古地震数据,为探讨该断裂带上大地震的重复行为提供了重要依据(邓起东等,1992;毛凤英,张培震,1995;冉勇康等,1997;闵伟等,2000;张培震等,2003).
2.1 海原断裂带的分段情况
断裂的分段活动性是指一条大的活动断裂带往往可以分成若干大的段落,每一段落都作为一个独立的震源而发生地震破裂,各段都具有独特的古地震活动历史(Schwartz,Coppersmith,1984).据张培震等(2003)的研究,根据断裂几何形态、地貌和活动习性,可以将海原断裂带分为西、中、东等3段.西段长100km,运动方式为左旋走滑,1920年海原地震在该段的地表左旋位移量平均为4m左右;中段长70km,走向WNW,倾向SSW,结构较为简单,活动性质亦以左旋走滑为主,1920年海原地震的主破裂沿该段发生,形成10m的最大左旋走滑位移;东段长60km,走向325°,与WNW走向的海原主断裂带相交角度达20°—25°,与西段和中段不同,该段除左旋走滑之外,还具有较大的逆冲挤压分量.
2.2 海原断裂带的古地震与破裂源
张培震等(2003)根据不同研究人员在海原断裂带上开挖的37个探槽数据,利用逐次限定方法进行分析,得到了3个分段断层上的古地震序列.由于7 000年前的古地震数据存在一定的缺失,本文中仅采用了距今7 000年以来海原断裂带上的古地震数据.根据3个段落的古地震活动图像,海原断裂带上共有3种破裂源:中段、西段和全段(包括东段).
海原断裂带西段上的高湾子地点三维探槽共揭露了5次古地震事件的位移量,由老至新的走滑位移量分别为(5.6±2.3)、(1.5±1.1)、(1.5±1.2)、(2±1)和(7±0.5)m(冉勇康等,1997).根据走滑位移量推断,在距今6 000多年有一次多段联合破裂事件,该地震事件很可能是与1920年海原大地震相同的全带联合破裂.而在这一破裂事件与1920年海原大地震的地震间隔期间,又有3次位移量为1—2m的次级破裂事件发生,显示出破裂的分级性.WD(6 910±585a)、MF (6 520±350a)和EA(6 120±950a)这3个古地震数据的时间范围交集为(6 595±275)a,与1920年海原大地震构成了一个全段破裂的轮回.根据以上分析结果及古地震数据,可以得到海原断裂带各种破裂源古地震发生时间的不确定性范围(表1).

表1 海原断裂带古地震发生时间的不确定性范围Table 1 The uncertainty of occurrence time of paleoearthquakes on Haiyuan fault
冉勇康和邓起东(1998)研究表明,沿海原断裂带主要活动段事件的强度分布表现出明显的特征地震行为,并且这种特征行为是分级的.此外,不同破裂源上的古地震事件均遵循准周期性的重复规律.因此,本文采用随机特征滑动模型来评估海原断裂带上强震发生概率的方法是可行的.
海原断裂带上的西段破裂和中段破裂属于次级破裂源,受全段破裂的控制,即虽然次级破裂具有相对独立的地震矩累积和释放过程,但全段破裂的发生会同时释放掉次级破裂上的地震矩累积量.再根据高湾子探槽揭露的5个事件的位移量推断,西段上的地震矩积累量一部分在次级破裂中释放,一部分在全段破裂中释放.亦即西段上积累的地震矩,要以一定的比例分配给两级破裂源(全段破裂和西段破裂).
3 海原断裂带震源参数的估计
利用随机特征滑动模型计算海原断裂带上的强震发生概率,需要确定不同破裂源上的平均特征震级和年平均地震矩累积率.
3.1 西段和中段破裂源上平均特征震级的估计
对于海原断裂带中段和西段上的平均特征震级,本文采用两种走滑型地震的矩震级MW-破裂面积A的经验关系式来估计.第一种是Working Group on California Earthquake Probabilities(2003)给出的适用于A≥500m2的关系式,即

第二种是Hanks和Bakun(2002)给出的适用于A≥468m2的关系式,即

对以上两种关系式分别赋予50%的权重,加权处理后可以计算得到海原断裂带西段和中段的平均特征震级.综合海原断裂带所在地区地质、地球物理等方面的资料(傅征祥,刘桂萍,1999;汤吉等,2005),本文取海原断裂带的下倾宽度W 为20km,再利用古地震数据所揭示的海原断裂带西段和中段破裂源的地表破裂长度,计算得到海原断裂带西段和中段破裂源的平均特征震级Mchar分别为7.5和7.3.本文采用与 Working Group on California Earthquake Probabilities(2003)相同的标准差(σM=0.24);为便于计算,本文在Mchar±0.5处进行截断.由于式(8)和(9)是否适用于MW>8.0地震尚需进一步论证,因此对于全段破裂,本文直接采用1920年海原地震的矩震级MW8.25作为其平均特征震级.
3.2 利用蒙特卡罗方法估计海原断裂带中段和西段破裂源上的年平均地震矩累积率
对于断层上年平均地震矩累积率的估计,一般利用平均滑动速率S与断层发震面积A的关系式来计算,即

式中μ为地壳岩石的剪切模量.本文中μ值取为3.3×1010N/m2.要计算断层的发震面积A就要确定断层长度L和下倾宽度W,而断层长度L和下倾宽度W 的确定均存在一定的误差;断层上的地震矩累积有一部分以中小地震和蠕滑的形式释放,这部分地震矩的比例很难确定,也具有很大的不确定性;再加上断层平均滑动速率测量的不确定性等等.这样得到的断层源上的地震矩累积率就会不够精确.此外,对于存在分级破裂的断层来说,更是很难确定次级破裂源上的地震矩累积率.
美国中小企业有较强的创新能力,闻岳春(2006)研究发现美国的中小企业在发展的过程中,政府不断出台小企业投资法或经济政策法等法案,给中小企业在法律层面较好的保障;其次,美国中小企业的内源融资占主导地位,VC、PE都在不断发展,新型融资方式不断出现,如众筹等给予中小企业丰富的融资渠道。
古地震事件缺乏精确的发生时间,存在较大的认知不确定性,若直接采用各个古地震事件发生时间测定的误差区间中值作为古地震发生时间,则会忽略掉这种不确定性.为此,Parsons(2008)提出了利用蒙特卡罗方法考虑这种认知不确定性.该方法根据已知的古地震序列及各次地震发生时间的不确定性范围,在其不确定性范围内进行反复随机抽样,进而生成大量的随机样本,这样就可以得到一个包含这种认知不确定的地震复发间隔数据的分布.
海原断裂带上古地震数据虽然较丰富,其中段和西段均有数个重复事件,但古地震事件均缺乏震级信息和精确的发生时间,无法利用“地震矩平衡”的原则推算出中段和西段破裂源上的年平均地震矩累积率.因此,本文参考Parsons(2008)对古地震发生时间认知不确定性的处理方法,利用蒙特卡罗方法随机生成大量地震复发间隔数据,然后以这些随机生成的地震复发间隔数据为基础,确定不同破裂源上的“最大可能”年平均地震矩累积率.
若在一定的地震矩累积率变化范围内任意选取一个年平均地震矩累积率˙M0,在古地震序列的时间不确定性范围内反复(10 000次)随机抽取各次古地震事件的发生时间,进而得到大量的地震复发间隔数据,同时还可以计算出相邻地震间的地震矩累积量和每次合成古地震的震级,这样就可以得到对应于该地震矩累积率的合成古地震震级分布.若随机生成的古地震事件震级分布的数学期望E(M)等于破裂源上的平均特征震级¯Mchar,则对应于该分布的年平均地震矩累积率即为本文所定义的“最大可能”年平均地震累积率.
在模拟过程中,海原断裂带中段上的MB和MD古地震事件往往会生成MW<6.8的地震事件,而MB和MD古地震事件在其中段两端的探槽中均有揭示(张培震等,2003),也即MB和MD事件的破裂长度大于60km.根据以往经验以及中段特征震级分布的下截断震级6.8,判定MB和MD古地震事件的矩震级MW不可能小于6.8.故在模拟过程中,当出现MW<6.8的事件时,则判定此次模拟失败,需重新模拟一次中段的古地震震级序列.
经过反复多次模拟,当海原断裂带西段破裂源和中段破裂源上的年平均地震矩累积率分别为1.24×1017N·m/a和1.31×1017N·m/a时,恰好使模拟生成的其西段和中段破裂源上的古地震震级分布的期望等于由式(8)和(9)计算得到的平均特征震级(图1,2).

图1 海原断裂带西段地震矩累积率˙M取值与合成古地震序列震级M分布的数学期望关系Fig.1 The relation between the value of seismic moment accumulation rate,˙M,and the expectant magnitude,M,of synthetic paleoearthquake events on the western segment of the Haiyuan fault zone

图2 海原断裂带中段地震矩累积率˙M取值与合成古地震序列震级M分布的数学期望关系Fig.2 The relation between the value of seismic moment accumulation rate,˙M,and the expectant magnitude,M,of synthetic paleoearthquake events on the middle segment of the Haiyuan fault zone
当海原断裂带中段破裂源和西段破裂源上的年平均地震矩累积率分别取值为1.31×1017N·m/a和1.24×1017N·m/a时,得到正态分布的标准差分别为0.06和0.18(图3,4).这反映了中段破裂源和西段破裂源上7 000年以来几次古地震震级的变异性与时间测定造成的误差.

图3 蒙特卡罗模拟得到的海原断裂带西段的古地震震级分布Fig.3 The magnitude distribution of paleoearthquakes on the western segment of the Haiyuan fault zone from Monte Carlo simulations

图4 蒙特卡罗模拟得到的海原断裂带中段的古地震震级分布Fig.4 The magnitude distribution of paleoearthquakes on the middle segment of the Haiyuan fault zone from Monte Carlo simulations
3.3 利用蒙特卡罗方法估计海原断裂带全段破裂源的年平均地震矩累积率
对于海原断裂带全段破裂源上年平均地震矩累积率的估计,由于1920年海原大地震的矩震级大小为已知,也即这个轮回内的地震矩累积量是确定的.根据“地震矩平衡”的原则(Working Group on California Earthquake Probabilities,2003),即在一个完整的轮回内地震矩的积累量应等于释放量,再考虑上一次全段破裂时间的不确定性及1920年海原大地震的震级大小,就可以用蒙特卡罗方法估计全段破裂源的最大可能年平均地震矩累积率.

图5 海原断裂带上的地震矩特征地震释放比θ估计值分布Fig.5 Distribution of estimates of the release ratio of seismic moment from characteristic earthquakes in the Haiyuan fault zone
利用蒙特卡罗方法模拟10万次古地震序列,记录下使1920年地震矩累积量对应的矩震级为M8.25(丁国瑜等,1993)时所取得θ值,并统计θ的分布.θ为0.6—1.2之间均匀分布的随机数,模拟过程中在MA和MW事件之前海原断裂带中段和西段上的地震矩累积率需减去上面给出的中段和西段破裂源上的年平均地震矩累积率,即减去次级破裂的释放量,分别为1.31×1017和1.24×1017N·m/a.最后得到满足中值为θ=0.93、标准差为0.04的正态分布(图5).这就得到了各段上最大可能的特征地震释放比为0.93.
根据海原断裂带地震矩累积率的特征地震释放比θ,可以得到去掉蠕滑和中小地震释放之后的其西段、中段和东段的地震矩累积率分别为2.75×1017、2.40×1017和2.02×1017N·m/a.而西段破裂源和中段破裂源上的年平均地震矩累积率分别为1.24×1017和1.31×1017N·m/a.由上述可知:去掉中小地震释放和断层蠕滑释放的地震矩后,中段上的地震矩累积率约为55%,以次级破裂的形式释放;西段上的地震矩累积率约为45%,以次级破裂的形式释放;剩余的地震矩以全段破裂的形式释放.
4 海原断裂带强震发生概率的计算
由于1920年海原大地震的离逝时间较短,海原断裂带西段和全段在未来100年后的地震矩累积量分别为2.54×1019和8.97×1019N·m,所对应的矩震级分别为6.89和7.27,而西段和全段破裂的下截断震级分别为7.00和7.75,这不足以使西段和全段发生特征地震形式的破裂;对于海原断裂带中段破裂的震级分布,参考本文所采用的震级MW-破裂面积A关系式,其平均特征震级Mchar取7.3,标准差σM取0.24,并在M¯char±0.5处进行截断.
根据式(4)和(7)可以计算得到海原断裂带中段强震发生概率密度分布函数(图6)和100年的条件概率(图7).其中概率密度分布函数f(T)满足参数为μlnT=6.752 9和σlnT=0.828 9的截断对数正态分布;而未来100年其中段破裂的概率P(MW≥6.8)=0.058 6.考虑随机特征滑动模型中离逝时间与矩震级之间的对应关系,可以对概率密度分布函数分震级档进行积分,再作归一化处理后可得到P(6.8≤MW<6.9)=0.015 8,P(6.9≤MW<7.0)=0.042 8,P(MW≥7.0)=0.

图6 海原断裂带中段强震发生的概率密度分布Fig.6 The probability density function of large earthquakes on the middle segment of the Haiyuan fault zone
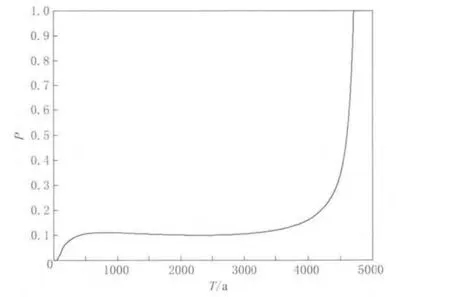
图7 海原断裂带中段100年条件概率分布Fig.7 The conditional probability for a 100-year exposure period on the middle segment of the Haiyuan fault zone
如图7所示,由随机特征滑动模型计算得到的海原断裂带中段100年条件概率在前一次特征地震发生之后2 750年左右时会逐渐提高,最后达到1.0.由于本文对所采用的震级分布进行了截断处理,即从保守角度考虑,假定不存在震级超过平均特征震级¯Mchar两倍标准差2σ的地震事件,则最后100年的条件概率达到1.0也是合理的.
在未来百年的强震发生概率的估计过程中,不可以同时考虑地震矩累积率和特征地震释放比θ的不确定性,因为θ的取值与不同破裂源上的震级不确定性具有一定的相关性,不是互相独立的参数.
5 讨论与结论
本文在弹性回跳理论的基础上,针对分段明确的断层源上强震发生的物理过程提出一种随机特征滑动模型.该模型不仅可以计算不同破裂源上的强震发生概率,还可以同时给出相应的震级分布.
若已确定平均特征震级,则可以根据有限的古地震数据,利用蒙特卡罗方法估计不同破裂源上的最大可能年平均地震矩累积率,为破裂源上的地震矩累积率的估计提供一种新方法.该方法可以确定次级破裂上地震矩累积率,而利用滑动速率则很难计算得到次级破裂源上的地震矩累积率.
海原断裂带上存在全段、中段和西段3种破裂源,其中中段和西段破裂属于次级破裂,受全段破裂的控制.次级破裂仅释放了该段上积累的部分地震矩累积量,很大一部分地震矩要在全段破裂中释放;全段破裂发生时,会同时释放掉次级破裂源上积累的地震矩,两级破裂源上的地震矩都要重新开始积累.
由于海原断裂带附近断裂上没有足够的古地震数据,本文没有考虑大地震诱发的库仑静应力场变化对附近断层上地震矩累积量的改变,而假定在每个特征地震复发间隔中断层源所受外界的影响是恒定的.
崔笃信,王庆良,胡亚轩,王文萍,朱桂芝.2009.用GPS数据反演海原断裂带断层滑动速率和闭锁深度[J].地震学报,31(5):516-525.
Cui D X,Wang Q L,Hu Y X,Wang W P,Zhu G Z.2009.Inversion of GPS data for slip rates and locking depths of the Haiyuan fault[J].Acta Seismologica Sinica,31(5):516-525(in Chinese).
邓起东,于贵华,叶文华.1992.地震地表破裂参数与震级关系的研究[G]∥活动断裂研究(2).北京:地震出版社:247-263.
Deng Q D,Yu G H,Ye W H.1992.Study on the relations between parameters of surface rupture and magnitude[G]∥Research on Active Faults(2).Beijing:Seismological Press:247-263(in Chinese).
丁国瑜,田勤俭,孔凡臣,谢霄峰,张立人,王立平.1993.活断层分段:原则、方法及应用[M].北京:地震出版社:30-37.
Ding G Y,Tian Q J,Kong F C,Xie X F,Zhang L R,Wang L P.1993.Segmentation of Active Fault:Principles,Methods and Application[M].Beijing:Seismological Press:30-37(in Chinese).
傅征祥,刘桂萍.1999.海原大地震可能触发古浪大地震的力学机制[G]∥中国地震学会成立20周年纪念文集.北京:地震出版社:234-243.
Fu Z X,Liu G P.1999.The mechanism of great Gulang earthquake triggered probably by the great Haiyuan earthquake[G]∥A Commemorative Collection of Papers for the 20th Anniversary of the Seismological Society of China.Beijing:Seismological Press:234-243(in Chinese).
毛凤英,张培震.1995.古地震研究中的逐次限定方法与新疆北部主要断裂带的古地震研究[G]∥活动断裂研究(4).北京:地震出版社:153-164.
Mao F Y,Zhang P Z.1995.Progressive constraining method in paleoseismic study and paleoearthquakes along the major active faults in northern Xinjiang[G]∥Research on Active Fault(4).Beijing:Seismological Press:153-164(in Chinese).
闵伟,张培震,邓起东.2000.区域古地震复发行为的初步研究[J].地震学报,22(2):163-170.
Min W,Zhang P Z,Deng Q D.2000.Primary study on regional paleoearthquake recurrence behavior[J].Acta Seismologica Sinica,22(2):163-170(in Chinese).
冉洪流,何宏林.2006.鲜水河断裂带北西段不同破裂源强震震级(M≥6.7)及复发间隔研究[J].地球物理学报,49(1):153-161.
Ran H L,He H L.2006.Research on the magnitude and recurrence interval of characterized earthquakes with M≥6.7 along the northwestern portion of the Xianshuihe fault zone in western Sichuan,China[J].Chinese Journal of Geophysics,49(1):153-161(in Chinese).
冉勇康,段瑞涛,邓起东,焦德成,闵伟.1997.海原断裂高湾子地点三维探槽的开挖与古地震研究[J].地震地质,19(2):97-107.
Ran Y K,Duan R T,Deng Q D,Jiao D C,Min W.1997.3-D trench excavation and paleoseismology at Gaowanzi of the Haiyuan fault[J].Seismology and Geology,19(2):97-107(in Chinese).
冉勇康,邓起东.1998.海原断裂的古地震及特征地震破裂的分级性讨论[J].第四纪研究,(3):271-278.
Ran Y K,Deng Q D.1998.Paleoearthquakes along Haiyuan fault and discussion of grading on rupture of large earthquakes[J].Quaternary Sciences,(3):271-278(in Chinese).
汤吉,詹艳,赵国泽,邓前辉,王继军,陈小斌,赵俊猛,宣飞.2005.青藏高原东北缘玛沁—兰州—靖边剖面地壳上地幔电性结构研究[J].地球物理学报,48(5):1205-1216.
Tang J,Zhan Y,Zhao G Z,Deng Q H,Wang J J,Chen X B,Zhao J M,Xuan F.2005.Electrical conductivity structure of the crust and upper mantle in the northeastern margin of the Qinghai-Tibet Plateau along the profile Maqěr-Lanzhou-Jingbian[J].Chinese Journal of Geophysics,48(5):1205-1216(in Chinese).
张培震,毛凤英.1996.活动断裂定量研究与中长期强地震危险性概率评价[G]∥活动断裂研究(5).北京:地震出版社:12-31.
Zhang P Z,Mao F Y.1996.A quantitative study of active fault and the long-and mid-term seismic risk evaluation[G]∥Research on Active Fault(5).Beijing:Seismological Press:12-31(in Chinese).
张培震,闵伟,邓起东,毛凤英.2003.海原活动断裂带的古地震与强震复发规律[J].中国科学:D辑,33(8):705-713.
Zhang P Z,Min W,Deng Q D,Mao F Y.2003.Paleoearthquake and strong earthquake recurrence of Haiyuan fault zone[J].Science China:Series D,33(8):705-713(in Chinese).
Aki K.1984.Asperities,barriers,characteristic earthquakes and strong motion prediction[J].J Geophys Res,89(B7):5867-5892.
Anderson J G,Wesnousky S G,Stirling M W.1996.Earthquake size as a function of fault slip rate[J].Bull Seismol Soc Am,86(3):683-690.
Ellsworth W L,Matthews M V,Nadeau R M,Nishenko S P,Reasenberg P A,Simpson R W.1999.A Physically Based Earthquake Recurrence Model for Estimation of Long-Term Earthquake Probabilities[R].Washington:U S Geological Survey:99-522.
Hanks T C,Kanamori H.1979.A moment-magnitude scale[J].J Geophys Res,84(B5):2348-2350.
Hanks T C,Bakun W H.2002.A bilinear source-scaling model for M-logAobservations of continental earthquakes[J].Bull Seismol Soc Am,92(5):1841-1846.
Leonard M.2010.Earthquake fault scaling:Self-consistent relating of rupture length,width,average displacement,and moment release[J].Bull Seismol Soc Am,100(5A):1971-1988.
Matthews M V,Ellsworth W L,Reasenberg P A.2002.A Brownian model for recurrent earthquakes[J].Bull Seismol Soc Am,92(6):2233-2250.
Panthi A,Shanker D,Singh H N,Kumar A,Paudyal H.2010.Time-predictable model applicability for earthquake occurrence in northeast India and vicinity[J].Nat Hazards Earth Syst Sci,11(3):993-1002.
Papazachos B C.1989.A time-predictable model for earthquake generation in Greece[J].Bull Seismol Soc Am,79(1):77-84.
Parsons T.2008.Appendix C:Monte Carlo Method for Determining Earthquake Recurrence Parameters From Short Paleoseismic Catalogs:Example Calculations for California.Open-File Rept 1437-C[R].Washington:U S Geological Survey:32.
Reid H F.1910.TheMechanicsoftheEarthquake,The California Earthquake of April 18,1906[R].Washington:State Investigation Commission,Carnegie Institution of Washington,(2):43-47.
Schwartz D P,Coppersmith K J.1984.Fault behavior and characteristic earthquakes:Examples from the Wasatch and San Andreas fault zones[J].J Geophys Res,89(B7):5681-5698.
Shanker D,Singh V P.1996.Regional time-and magnitude-predictable seismicity model for north-east India and vicinity[J].Acta Geod Geoph Hung,31(1/2):181-190.
Shimazaki K,Nakata T.1980.Time-predictable recurrence model for large earthquakes[J].Geophys Res Let,7(4):279-282.
Wells D L,Coppersmith K J.1994.New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J].Bull Seismol Soc Am,84(4):974-1002.
Wesnousky S G.1986.Earthquakes,Quaternary faults,and seismic hazard in California[J].J Geophys Res,91(B12):12587-12631.
Wesnousky S G.1994.The Gutenberg-Richter or characteristic earthquake distribution,which is it?[J].Bull Seismol Soc Am,84(6):1940-1959.
Working Group on California Earthquake Probabilities.2003.Earthquake Probabilities in the San Francisco Bay Region:2002 to 2031.Open-File Rept 03-214[R].Washington:U S Geological Survey.
Youngs R R,Coppersmith K J.1985.Implications of fault slip rates and earthquake recurrence models to probabilistic seismic hazard estimates[J].Bull Seismol Soc Am,75(4):939-964.
