裂缝介质旋转交错网格正演模拟
2014-12-17吴国忱秦海旭
吴国忱 秦海旭
(中国山东青岛266580中国石油大学(华东)地球科学与技术学院)
引言
全球发现的油气藏中有大量的裂缝性油气藏,包括碳酸盐裂缝型油气藏、致密砂岩裂缝型油气藏及基岩裂缝型油气藏(毛宁波等,2008;杨晓等,2010).裂缝通常是裂缝性油气藏的储存空间或运移通道,因此裂缝介质中地震波场的研究越来越受到关注(谢桂生,1994;金抒辛,何樵登,2005;潘保芝等,2006).研究发现,在含有定向分布的裂缝介质中地震波的传播呈现各向异性的特征(张中杰,何樵登,1989;郭建,1993;Schoenberg,Sayers,1995).因此,利用地震波场来研究裂缝发育带位置、确定储层物性并进行储层预测具有重要的意义.
目前研究裂缝的方法之一是将裂缝看成散射体,用散射理论研究裂缝介质的地震响应(刁顺等,1994a,b),但此方法的正演效率非常低.本文用等效理论将裂缝介质等效为各向异性介质,运用各向异性介质理论研究裂缝的地震响应.各向异性是指介质的弹性参数随方向而变化,该方法效率高,能得到较好的效果.裂缝对地震波的影响已研究了多年.例如:Hudson(1981)提出裂缝介质中P波和S波速度与衰减的公式;Thomsen(1986)提出利用弹性弱各向异性理论研究定向裂缝与等径孔隙度对地震速度的综合影响;Schoenberg和Sayers(1995)使用裂缝法向与切向柔度推导裂缝介质中的有效弹性常数;Bakulin等(2000a,b,c)回顾了几种不同的裂缝等效理论,并比较了它们对裂缝参数估计的可行性.
地震波场数值模拟是地球物理学领域的一个研究热点,既可以提高我们对各种复杂介质中地震波传播规律的认识,又可以作为检测工具检验各种方法技术的应用效果.前人研究结果表明,地震波在定向裂缝介质中的传播具有横向各向同性的特征(Hudson,1981;Thomsen,1986;Bakulin et al,2000a,b,c).Crampin(1985)提出构造应力产生的具有水平对称轴的横向各向同性(horizontal transverse isotropy,简称为HTI)介质,可用来模拟高陡倾角裂缝介质(孔丽云等,2012).目前常用的裂缝介质正演模拟方法主要是交错网格有限差分方法(董良国等,2000;裴正林,2004,2006;裴正林,王尚旭,2005;李雪静,刘定进,2008).普通交错网格能有效地模拟地震波在裂缝介质中的传播,但也存在一定的缺点.首先,当模拟非均匀性比较强的介质或各向异性介质时,为了获得满意的计算结果,需要对介质参数进行平均或内插;其次,在遇到自由界面时,必须对自由界面进行单独的显式处理(严洪勇,刘洋,2012).旋转交错网格将相同的物理量定义在相同的网格点上,计算其沿对角线的差分,然后利用对角线差分组合计算其沿坐标轴的差分.该方法不需要对介质参数进行平均或内插,在遇到自由边界时不需要单独的显示处理(Saenger et al,2000),从而解决了普通交错网格存在的缺点,是目前正演中比较准确的方法.本文采用旋转交错网格正演模拟方法对裂缝性储集层进行正演模拟.
1 裂缝介质的等效理论
运用各向异性理论进行裂缝介质正演模拟,需要将裂缝介质等效为各向异性介质.目前广泛存在的裂缝等效理论主要有Thomsen等效理论、Hudson等效理论及线性滑动理论等.Thomsen等效理论相当于低频模型,假设流体流动无限慢,该方法限制条件较多,不利于研究(Thomsen,1986).Hudson等效理论与Thomsen等效理论正好相反,相当于高频模型,其假设流体流动无限快,也不利于实际研究(Hudson,1999).线性滑动理论(Bakulin et al,2000a,b,c)是将裂缝看作地层中的一个柔性面,该柔性面可以用裂缝的切向柔度和法向柔度进行表示,柔度符合线性滑动边界条件便于求解.对于多组裂缝可以对裂缝柔度进行矢量叠加便于实际求解.因此本文采用线性滑动等效理论将裂缝介质等效为各向异性介质.
含有裂缝岩石的总柔度等于裂缝柔度与围岩柔度的和,即

式中,S为岩石总的柔度矩阵.Sf为裂缝的柔度矩阵.Sb为围岩的柔度矩阵.其中柔度矩阵为弹性矩阵C的倒数,即S=C-1.根据线性滑动理论,裂缝介质的弹性矩阵为

式中,λ和μ为背景岩石的拉梅常数,ΔN和ΔT分别为裂缝介质的法向柔度与切向柔度.当介质中存在几组裂缝时,先求出每组裂缝介质的切向柔度与法向柔度,然后对切向柔度与法向柔度进行矢量叠加求出裂缝介质总的柔度矩阵.裂缝介质等效示意图如图1所示.
由于裂缝介质的法向柔度与切向柔度需要满足线性滑动边界条件,不方便求解.而采用Hudson等效理论与线性滑动理论相结合,既弥补了Hudson等效理论的局限性,又可以方便计算裂缝的法向柔度与切向柔度.实际计算中采用线性滑动理论与Hudson理论相结合的等效理论将裂缝介质等效为各向异性介质.此时,裂缝的法向柔度和切向柔度分别为
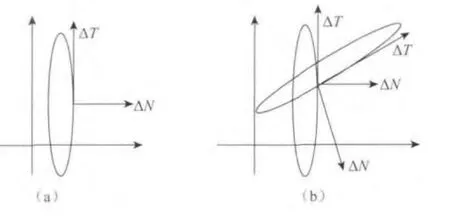
图1 裂缝介质等效示意图图中ΔN和ΔT分别为裂缝介质的法向柔度与切向柔度.(a)单缝模型;(b)裂缝组合模型Fig.1 The sketch of fracture equivalence ΔNdenotes the normal weakness,and ΔTdenotes the tangential weakness(a)Sigle fracture model;(b)Combination model of fractures

式中,e为裂缝密度,k′和μ′分别为裂缝充填物的体积模量与切变模量,k为背景介质的体积模量,a为裂缝的长度,c为裂缝的宽度,g=v2S/v2P.弹性介质模型的性质由刚度矩阵C确定,C确定了应力与应变之间的关系,但其确定弹性波动方程系数的物理意义很不直观.Thomsen(1986)提出了一整套表征各向异性的参数,具体表达如下:

式中VP0,VS0分别为qP波和qS波沿各向异性介质对称轴方向的相速度;ε,δ和γ是表示HTI介质各向异性强度的3个无量纲因子.根据式(1)-(4)可得裂缝参数与各向异性参数之间的关系为

将线性滑动理论与Hudson等效理论相结合,对4组典型的裂缝介质进行简单的等效,其结果如表1所示.裂缝层埋深3 000m,岩层厚度为100m,背景岩石的纵波速度为6 200m/s,横波速度为3 500m/s,密度为2 800kg/m3.

表1 裂缝介质参数Table 1 Fracture parameters
2 HTI介质一阶速度应力方程
式(2)—(3)可将裂缝参数等效为表征裂缝介质的弹性矩阵参数,即将裂缝介质等效为各向异性介质.下面推导HTI介质的一阶速度应力方程.由广义胡克定律、运动微分方程及几何方程可得HTI介质的波动方程.
广义胡克定律

运动微分方程

几何方程

式中,U=(ux,uy,uz)为地震波场,F=(fx,fy,fz)为震源,L为偏微分算子,ρ为密度,

根据式(6)—(8)可以求得HTI介质一阶速度应力方程的表达式为
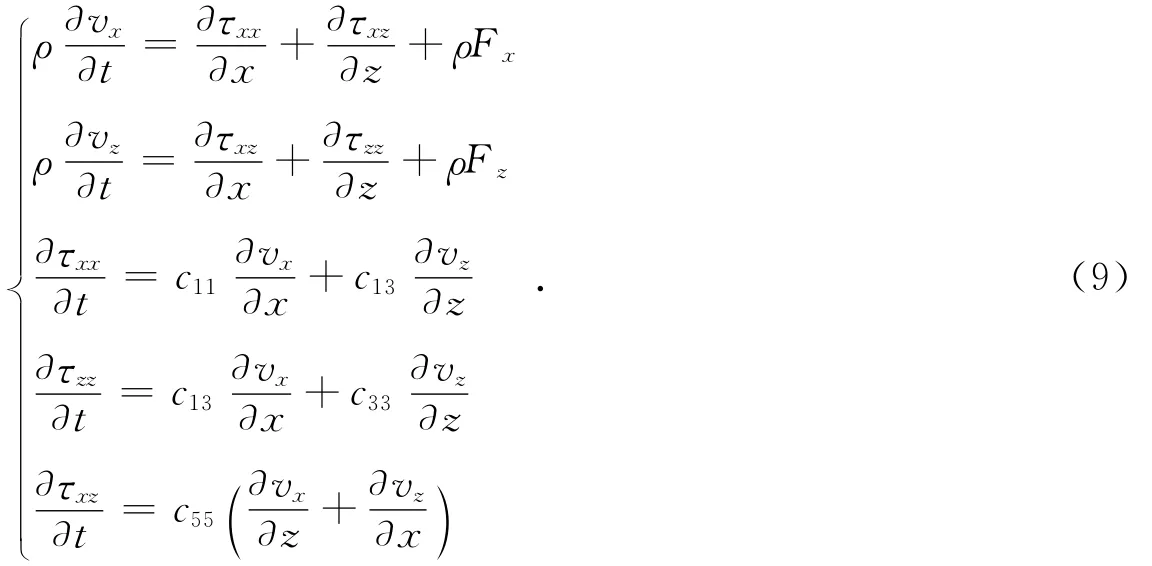
3 裂缝介质旋转交错差分方程
3.1 时间2阶差分方程近似

3.2 空间高阶差分方程近似

式中,Δx为x方向的采样间隔,cn为有限差分系数,具体如表2所示.

表2 几种常用有限差分系数Table 2 Several kinds of finite difference coefficients
3.3 一阶速度应力差分方程
交错网格主体网格定义的变量与交错网格半定义的变量不同,速度、应力和弹性参数的定义规则如图2所示.其中变量分别定义在网格1,2,3,4点上.
在普通交错网格有限差分中,通常将介质参数定义在法向应力所在的网格点上.本文中法向应力及所有的背景参数都定义在主体网格1点上,z方向速度定义在2点上,x方向速度定义在3点上,切应力定义在4点上.应用普通交错网格需要定义1套主网格点和3套半网格点,在模拟裂缝介质传播时需要内插相关的弹性参数.应力速度及背景参数的定义规则如表3所示.其中:正应力τxx,τzz以及弹性参数c11,c13,c55,c33,ρ定义在主体网格1点上;切应力τxz定义在4点所示的半网格点上,z方向速度vz定义在2点所示的半网格点上;x方向速度vx定义在3点所示的半网格点上;半网格3点的密度需要用密度差值移位或者取平均得到.

图2 标准交错网格示意图Fig.2 The sketch of standard staggered grid

图3 旋转交错网格示意图Fig.3 The sketch of rotated staggering grid

表3 标准交错网格中弹性波场分量和弹性参数的空间位置Table 3 The positions of elastic wavefield components and elastic parameters in standard staggered grid

表4 旋转交错网格中弹性波场分量和弹性参数的空间位置Table 4 The positions of elastic wavefield components and elastic parameters in rotated staggering grid
当介质非均质非常强时,普通交错网格有限差分得不到满意的结果,此时需要用旋转交错网格模拟.旋转交错网格首先将图2沿对角线旋转,使得所有的应力分量位于同一点上,所有的速度位于同一点上.本文的变量定义规则如图3所示.每个点代表的变量含义如表4所示.
旋转交错网格中所有速度分量和应力分量均位于相同的网格点上,因此介质密度与弹性参数均位于速度所在的网格点或者应力所在的网格点上.旋转交错网格中只需要定义一套主体网格和一套半网格,在模拟裂缝介质地震波场传播时不需要对弹性参数进行内插,从而提高了稳定性.旋转交错网格中速度应力参数及背景参数如表4所示.
表4给出了应力速度及背景参数的定义规则.其中正应力τxx和τzz、切应力τxz以及弹性参数c11,c13,c55,c33,ρ均定义在主体网格1点上,x方向速度vx与z方向速度vz定义在2点所示的半网格点上.旋转交错网格将相同的物理量定义在相同的网格点上,计算其沿对角线的差分,再利用对角线差分组合计算其沿坐标轴的差分.此方法不需要对介质参数进行平均或者差值.下面推导二维情况下旋转交错网格沿坐标轴方向的表达式.
根据矢量合成有

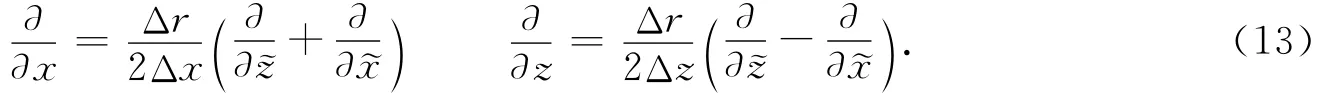
将式(12)、(13)带入式(9),得到旋转交错网格下裂缝介质的一阶速度应力方程与一阶应力速度方程为

式(14)中只需要用到对角线方向的差分格式,将对角线的差分格式进行线性组合即可得到最终的结果.将式(11)带入式(14)得

式(15)即为变量u对˜x,˜z的差分,将变量u换成速度分量和应力分量便可得到式(14)的差分格式,进行正演模拟即可得到裂缝介质的波场响应特征.
3.4 正演模拟中需要注意的问题
3.4.1 稳定性条件
对于裂缝介质一阶速度应力方程与一阶应力速度差分方程而言,得到其稳定性的解析式比较困难.通过矩阵特征分析(Igel et al,1995)可得到其稳定性的一种表达形式.通过矩阵特征分析法得到裂缝介质一阶速度应力弹性波方程时间(2阶)、空间(10阶)的稳定性条件为
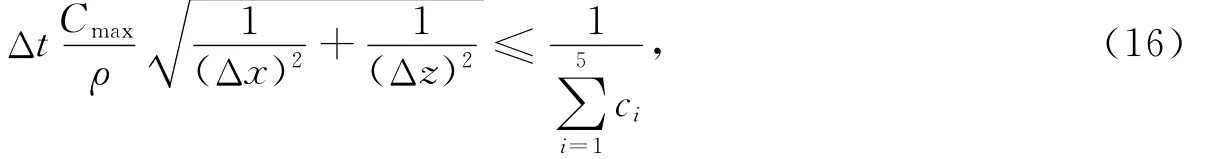
式中,Δt为时间采样间隔,Cmax为弹性矩阵最大值,ρ为密度,Δx和Δz为空间采样间隔,ci为差分系数(表2).若选取参数不正确,程序不稳定,会使得正演模拟结果错误,消除的方法是根据模型参数通过式(16)选取合适的时间空间采样间隔.须说明,时间采样点不是越小越好,时间采样点越小则需要的时间点数越多,累计误差越大,也会引起不稳定且计算时间太长,不利于实际研究.
3.4.2 边界条件
采用有限差分进行裂缝介质正演模拟的过程中,由于模拟区域不是无限大,这种人为限定模型计算区域的方法会引起边界问题.这种边界引起的反射波常常比物理边界更强,在地震记录中会对有效信息产生干扰,因此针对边界问题必须采用一定的边界条件消除这种边界反射(何燕,2008).消除边界反射的方法有很多,其中具有代表性的有:Clayton和Engquist(1977)基于旁轴近似提出了吸收边界条件,其在特定的入射角和频率范围内具有较好的吸收效果;Reynolds(1978)提出了透明边界条件,其特点是零角度入射时反射系数为零;Marfurt(1984)提出了海绵边界条件;Berenger(1994)针对电磁波传播情况提出了最佳匹配层(perfectly matcher layer,简称PML)吸收边界条件,其在海绵吸收边界的基础上作了进一步改进,并从理论上证明了该方法可以完全吸收来自各个方向的各种频率波,且不产生任何反射,是目前应用最广泛的边界条件.本文采用PML边界条件消除边界反射.该方法的原理是在研究区域的边界上增加一个吸收层,使边界上传入吸收层的波随传播距离的增加成指数衰减,而不产生任何边界反射,可以得到裂缝介质一阶速度应力带有PML边界的差分格式.旋转交错网格的PML边界条件与普通交错网格的PML边界条件一致.下面以普通交错网格方程推导PML边界条件,然后再应用于旋转交错网格.以公式(9)中其中一个方程(省略震源)为例,

根据复数坐标变换

对式(17)两边进行傅里叶变换得

根据波场分解原理,式(19)可分解为

将式(18)带入式(20),并进行傅里叶反变换得

式(9)中其余方程的推导过程如上,不再一一重复.
3.4.3 网格频散
采用有限差分法存在固有缺陷,即在利用有限差分算子逼近微分算子时会产生误差项,它使得具有不同频率的地震波表现为不同的相速度,从而使地震波发生频散,影响数值模拟的精度和偏移成像效果.数值频散实质上是一种因离散化求解波动方程而产生的伪波动,它是指组成地震波的不同频率分量以不同的速度传播,随着传播时间的推移地震波扩展为更长波列的现象(孙成禹等,2009).时间网格频散表现为相速度超前,空间网格频散表现为相速度滞后.本文采用通量传输校正方法(Book et al,1975;Boris,Book,1973)消除频散,因为使用空间高阶有限差分方法会压制频散且计算量非常大.通量传输校正方法主要分为以下几步:
1)输运计算,计算待修正值

2)求n时刻的扩散通量

式中η1为扩散系数.
3)扩散计算

4)反扩散通量计算

式中η2为反扩散系数.
5)限制反扩散通量条件

6)反扩散计算

4 裂缝介质正演模拟分析
采用式(14)、(15)的差分方程,编写程序进行裂缝介质正演模拟,可以得到裂缝介质的正演模拟记录.其中模拟过程中需要注意边界条件、频散压制及稳定性条件.裂缝引起的反射波能量相对于背景介质较小,因而正演模拟中裂缝介质引起的反射系数变化经常被淹没在背景介质中.为了研究裂缝介质的波场,本文设计一个均匀模型裂缝位于均匀模型中间,如图4所示.模型尺寸为4 000m×4 000 m,纵向、横向网格间距均为10m,纵波速度为3 000m/s,横波速度为1 700m/s,密度为2 000 kg/m3.黑色区域为裂缝所在的区域,其中:裂缝长度为5m,宽度为1mm,密度为2条/m,裂缝充填物为油;裂缝横向延伸为4 000m、纵向延伸为100m.采用式(14)、(15)的差分方程进行正演模拟.正演模拟采用雷克子波,子波的主频为25Hz,时间采样率为1ms,时间长度为5s.正演模拟结果如图5所示.

图4 单层模型示意图Fig.4 The sketch of single layer model
图5 中由于裂缝引起的各向异性较小,qSV波和qSH波在地震波场中无法区分,统一用qS波表示.从图5a中可以看出,t=0.75s时波还没有传播到裂缝处,地震波场中含有两种波,即qP波和qS波.其中qP和qS分别为准P波和准S波.从图5b可以看出,t=1.0s时qP波已经穿过裂缝层,地震波场中含有qS波、qPRqP波(qP波入射qP反射波)、qPRqS波(qP波入射qS反射波)、qPTqS波(qP波入射qS透射波)及qPTqP波(qP波入射qP透射波).地震波场比较复杂,可以看出裂缝介质顶底都会产生反射波、透射波.从图5c中可以看出,t=1.6s时qS波已经穿过裂缝层,地震记录中含有qPRqP波(qP波入射qP反射波)、qPRqS波(qP波入射qS反射波)、qSRqP波(qS波入射qP反射波)、qSRqS波(qS波入射qS反射波)、qPTqS波(qP波入射qS透射波)、qPTqP波(qP波入射qP透射波)、qSTqS波(qS波入射qS透射波)及qSTqP波(qS波入射qP透射波).由此可见,t=1.6s时地震波场非常复杂,裂缝介质顶底都会产生反射波、透射波.地震波穿过裂缝介质时地震波场非常复杂,便于我们利用地震波场的信息反演裂缝的参数.

图5 不同时刻地震波场示意图.(a)t=0.75s;(b)t=1.0s;(c)t=1.6sFig.5 The sketch of seismic wavefield in different moments.(a)t=0.75s;(b)t=1.0s;(c)t=1.6s
同样采用图4模型示意图,模型尺寸改为400m×400m,模型采样间隔为10m×10m.采用主频为75Hz的雷克子波,时间采样率为0.1ms,时间长度为0.5s,炮点位于模型中间.模型纵波速度为3 000m/s,横波速度为1 700m/s.黑色区域为裂缝所在的区域,其中:裂缝长度为5m,宽度为1mm,密度为2条/m,裂缝充填物为油;裂缝横向延伸为400m,纵向延伸为1—24m.从地震记录中提取第50道的PP波和SS波记录,如图6所示.

图6 不同裂缝延伸长度的单道地震记录.(a)PP波;(b)SS波Fig.6 Seismic records of single trace in different crack growth.(a)PP wave;(b)SS wave
根据正演采用的参数,纵波的波长为40m,横波的波长为23m.由图6a可知,当裂缝延伸为纵波半个波长时,顶底反射完全分开;当裂缝延伸为纵波1/4波长时,可以找出顶底反射界面,此时顶底反射波尚未完全分开.由图6b可知,当裂缝延伸为横波半个波长时,顶底反射完全分开;当裂缝延伸为横波1/4波长时,可以找出顶底反射界面,此时顶底反射波尚未完全分开.
为了更清楚地了解裂缝介质对地震波场的影响,从不同的裂缝参数出发研究不同裂缝参数对地震波场的影响.下面分别研究裂缝密度、裂缝纵横比、裂缝充填物等裂缝参数对地震波场的影响.
4.1 裂缝密度对地震波场的影响
采用图4所示的模型示意图.裂缝长度为2m,宽度为1mm,裂缝充填物为油;裂缝密度分别为0.5,1,2,4和5条/m;采用雷克子波进行正演模拟,子波的主频为25Hz,时间采样率为1ms,时间长度为5s.正演模拟结果如图7所示.可以看出,裂缝密度越大,引起的反射波能量越强.

图7 不同裂缝密度(e)正演模拟的地震记录(a)e=0.5条/m;(b)e=1条/m;(c)e=2条/m;(d)e=4条/m;(e)e=5条/mFig.7 Seismic records in the media with different fracture densities(a)e=0.5m-1;(b)e=1m-1;(c)e=2m-1;(d)e=4m-1;(e)e=5m-1
4.2 裂缝纵横比对地震波场的影响
采用图4所示的模型示意图.裂缝密度为1条/m,裂缝充填物为油,裂缝纵横比分别为1 000,2 000,5 000,7 000和10 000;采用雷克子波进行正演模拟,子波的主频为25Hz,时间采样率为1ms,时间长度为5s.正演模拟结果如图8所示.可以看出,裂缝纵横比越小,引起的反射波能量越强.
4.3 裂缝充填物对地震波场的影响
采用图4所示的模型示意图.裂缝密度为1条/m,长度为2m,宽度为1mm,裂缝充填物分别为油、水和泥岩;采用雷克子波进行正演模拟,子波的主频为25Hz,时间采样率为1ms,时间长度为5s.正演模拟结果如图9所示.可以看出,裂缝充填物速度与背景速度差别越大,引起的反射波能量越强.

图8 不同裂缝纵横比(a/c)正演模拟的地震记录(a)a/c=1000;(b)a/c=2000;(c)a/c=5000;(d)a/c=7000;(e)a/c=10000Fig.8 Seismic records in the media with different fracture aspect ratios(a)a/c=1000;(b)a/c=2000;(c)a/c=5000;(d)a/c=7000;(e)a/c=10000

图9 不同裂缝充填物正演模拟的地震记录(a)油;(b)水;(c)泥岩Fig.9 Seismic records in the media with different fracture fillings(a)Oil;(b)Water;(c)Mudstone
5 讨论与结论
本文提出一种高陡倾角裂缝介质的正演模拟方法.利用裂缝等效理论将高陡倾角裂缝介质等效为横向各向同性(HTI)介质,推导出HTI介质旋转交错网格一阶速度应力方程及所对应的差分方程,实现了裂缝介质的正演模拟,分析了裂缝介质中的地震波场响应特征,讨论了不同裂缝密度、裂缝纵横比和裂缝充填物的地震响应特征.结果表明:裂缝的存在相当于人为增加反射界面;裂缝密度越大,裂缝纵横比越小,裂缝充填物与背景介质弹性性质差别越大,引起的反射波能量变化越大.本文模拟结果为利用地震数据进行裂缝介质参数反演与储层识别及预测提供了依据.需要说明的是:本文结果仅仅针对一组高陡倾角裂缝介质,而实际地层中裂缝的存在形式是多种多样的,需进一步研究实际裂缝介质中的地震波场特征;本文仅仅对裂缝充填物、裂缝密度、裂缝纵横比等裂缝物性参数进行了正演模拟,需要进一步研究裂缝介质其它物性参数的地震响应特征;本文使用弹性波进行正演模拟,而实际地震记录通常是纵波记录,因此需要进一步研究各向异性介质中纵横波分离的问题.
刁顺,杨慧珠,许云.1994a.裂缝及介质非均匀散射[J].石油物探,33(4):49-55.
Diao S,Yang H Z,Xu Y.1994a.Scattering due to inhomogeneity of media[J].Geophysical Prospecting for Petroleum,33(4):49-55(in Chinese).
刁顺,杨慧珠,许云.1994b.TI介质裂纹散射研究[J].石油地球物理勘探,29(5):545-551.
Diao S,Yang H Z,Xu Y.1994b.Research on crack scattering in transversally isotropic medium[J].Oil Geophysical Prospecting,29(5):545-551(in Chinese).
董良国,马在田,曹景忠,王华忠,耿建华,雷冰,许世勇.2000.一阶弹性波方程交错网格高阶差分解法[J].地球物理学报,43(3):411-419.
Dong L G,Ma Z T,Cao J Z,Wang H Z,Geng J H,Lei B,Xu S Y.2000.A staggered-grid high-order difference method of one-order elastic wave equation[J].Chinese Journal of Geophysics,43(3):411-419(in Chinese).
郭建.1993.裂隙介质中的各向异性研究[J].石油地球物理勘探,28(3):348-353.
Guo J.1993.A research into anisotropy of fractured medium[J].Oil Geophysical Prospecting,28(3):348-353(in Chinese).
何燕.2008.正交各向异性弹性波高阶有限差分正演模拟研究[D].东营:中国石油大学(华东)地球资源与信息学院:55-58.
He Y.2008.High-Order Finite-Difference Forward Modeling of Elastic-Wave in Orthorhombic Anisotropic Media[D].Dongying:College of Geo-resources and Information,China University of Petroleum:55-58(in Chinese).
金抒辛,何樵登.2005.泥岩裂隙的正演模拟方法研究[J].石油物探,44(2):119-127.
Jin S X,He Q D.2005.Forward modeling method research on mudstone fractures medium[J].Geophysical prospecting for Petroleum,44(2):119-127(in Chinese).
孔丽云,王一博,杨慧珠.2012.裂缝诱导HTI双孔隙介质中的裂缝参数分析[J].地球物理学报,55(1):189-196.
Kong L Y,Wang Y B,Yang H Z.2012.Fracture parameters analyses in fracture-induced HTI double-porosity medium[J].Chinese Journal of Geophysics,55(1):189-196(in Chinese).
李雪静,刘定进.2008.各向同性介质弹性波交错网格有限差分正演模拟[J].小型油气藏,13(3):15-20.
Li X J,Liu D J.2008.Isotropic medium elastic wave cross grid finite difference forward simulation[J].Small Hydrocarbon Reservoirs,13(3):15-20(in Chinese).
毛宁波,谢涛,杨凯,金明霞.2008.裂缝储层地震方位AVO正演模拟研究及应用[J].石油天然气学报,30(5):59-63.
Mao N B,Xie T,Yang K,Jin M X.2008.Azimuthal AVO forward model for fracture reservoirs and its application[J].Journal of Oil and Gas Technology,30(5):59-63(in Chinese).
潘保芝,张丽华,单刚义,杨雪.2006.裂缝和孔洞型储层孔隙模型的理论进展[J].地球物理学进展,21(4):1232-1237.
Pan B Z,Zhang L H,Shan G Y,Yang X.2006.Progress in porosity model for fractured and vuggy reservoirs[J].Progress in Geophysics,21(4):1232-1237(in Chinese).
裴正林.2004.三维各向异性介质中弹性波方程交错网格高阶有限差分法数值模拟[J].石油大学学报:自然科学版,28(5):23-29.
Pei Z L.2004.Three-dimensional numerical simulation of elastic wave propagation in 3-D anisotropic media with staggered-grid high-order difference method[J].Journal of China University of Petroleum:Edition of Natural Science,28(5):23-29(in Chinese).
裴正林,王尚旭.2005.任意倾斜各向异性介质中弹性波波场交错网格高阶有限差分法模拟[J].地震学报,27(4):441-451.
Pei Z L,Wang S X.2005.A staggered-grid high-order finite-difference modeling for elastic wave field in arbitrary tilt anisotropic media[J].Acta Seismologica Sinica,27(4):441-451(in Chinese).
裴正林.2006.双相各向异性介质弹性波传播交错网格高阶有限差分法模拟[J].石油地球物理勘探,41(2):137-143.
Pei Z L.2006.Staggered grid high-order finite-difference modeling of elastic wave transmission in biphase anisotropic medium[J].Oil Geophysical Prospecting,41(2):137-143(in Chinese).
孙成禹,宫同举,张玉亮,张文颖.2009.波动方程有限差分法中的频散与假频分析[J].石油地球物理勘探,44(1):43-48.
Sun C Y,Gong T J,Zhang Y L,Zhang W Y.2009.Analysis on dispersion and alias in finite-difference solution of wave equation[J].Oil Geophysical Prospecting,44(1):43-48(in Chinese).
谢桂生.1994.裂隙裂缝介质的弹性波模拟[J].石油地球物理勘探,29(5):537-544.
Xie G S.1994.Simulation of elastic waves in fractured medium[J].Oil Geophysical Prospecting,29(5):537-544(in Chinese).
严洪勇,刘洋.2012.黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J].地球物理学报,55(4):1354-1365.
Yan H Y,Liu Y.2012.Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J].Chinese Journal of Geophysics,55(4):1354-1365(in Chinese).
杨晓,王真理,喻岳钰.2010.裂缝型储层地震检测方法综述[J].地球物理学进展,25(5):1785-1794.
Yang X,Wang Z L,Yu Y Y.2010.The overview of seismic techniques in prediction of fracture reservoir[J].Progress in Geophysics,25(5):1785-1794(in Chinese).
张中杰,何樵登.1989.含裂隙介质中地震波运动学问题的正演模拟[J].石油地球物理勘探,24(3):290-299.
Zhang Z J,He Q D.1989.Forward modeling of kinematic problems of seismic wave in fractured medium[J].Oil Geophysical Prospecting,24(3):290-299(in Chinese).
Bakulin A,Grechka V,Tsvankin L.2000a.Estimation of fracture parameters from reflection seismic data.Part 1:HTI model due to a single fracture set[J].Geophysics,65(6):1788-1802.
Bakulin A,Grechka V,Tsvankin L.2000b.Estimation of fracture parameters from reflection seismic data.Part 2:Fractured models with orthorhombic symmetry[J].Geophysics,65(6):1803-1817.
Bakulin A,Grechka V,Tsvankin L.2000c.Estimation of fracture parameters from reflection seismic data.Part 3:Fractured models with monoclinic symmetry[J].Geophysics,65(6):1818-1830.
Berenger J P.1994.A perfectly matched layer for the absorption of electromagnetic waves[J].J Comput Phys,114(2):185-200.
Boris J P,Book D L.1973.Flux-corrected transport.Ⅰ.SHASTA,a fluid transport algorithm that works[J].J Computat Phys,11(1):38-69.
Book D L,Boris J P,Hain K.1975.Flux-corrected transportⅡ:Generalizations of the method[J].J Computat Phys,18(3):248-283.
Clayton R,Engquist B.1977.Absorbing boundary conditions for acoustic and elastic wave equations[J].Bull Seismol Soc Am,67(6):1529-1540.
Crampin S.1985.Evaluation of anisotropy by shear-wave splitting[J].Geophysics,50(1):142-152.
Hudson J A.1981.Wave speeds and attenuation of elastic waves in material containing cracks[J].Geophysics,64(1):133-150.
Igel H,Mora P,Riollet B.1995.Anisotropic wave propagation through finite-difference grids[J].Geophysics,60(4):1203-1216.
Marfurt K J.1984.Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J].Geophysics,49(5):533-549.
Reynolds A C.1978.Boundary conditions for the numerical solution of wave propagation problems[J].Geophysics,43(6):1099-1110.
Saenger E H,Gold N,Shapiro S A.2000.Modeling the propagation of elastic waves using a modified finite-difference grid[J].Wave Motion,31(1):77-92.
Schoenberg M,Sayers C M.1995.Seismic anisotropy of fractured rock[J].Geophysics,60(1):204-221.
Thomsen L.1986.Weak elastic anisotropy[J].Geophysics,51(10):1954-1966.
