基于MapReduce框架的BCH码并行译码研究

陆忠敏， 孙 建， 张家精

（1．安徽城市管理职业学院基础部，合肥 230011；2．安徽省电力科学研究院，合肥 230609，3．安徽建筑大学数理学院 合肥 230601）

1 前言

BCH码［1，2］的译码问题一直是研究的热点，同时也是BCH码应用中的关键问题。经典的BCH译码算法一般采用迭代方法计算错误多项式的根，如BM迭代算法［3］，迭代算法涉及大量的线性方程组的分解计算。在实践上一般采用串行译码的方式，有着电路设计复杂，译码速度慢的特点。

在大数据［4］环境下，由于数据量巨大，数据的串行、迭代译码的方式显然无法满足应用的要求。本文提出了一种基于分布式并行框架（MapRe－duce）［5］的BCH 码查找表译码算法［6］、设计了该算法的译码方案并进行了对比分析。

2 BCH码译码算法与分布式框架

2．1 译码原理

BCH 码［1，2］是循环码的一个非常重要的子集，先 后 由 Hocquenghem、Bose和 Reychaudhuri几乎同时并独立提出以他们三人名字的首字母而命名的循环纠错码。由循环码的定义可知，GF（q）（q为素数或素数的幂）上的［n，k］循环码中，存在并且唯一存在有n－k次的首一多项式

（1）BCH码的结构

令α是扩域GF（2m）中的本原元素，应将纠t个差错的BCH码的生成多项式选取连续的2t个α，α2，…，α2t都是它的根，即它们也是每个码字的根。按上述定义得到的码叫做本原BCH码。对于任何正整数m和t，存在一个下列参数的二元BCH码:码长:n＝2m－1；一致校验位数目:n－k≤mt；最小距离:dmin≥2t＋1。

（2）一般迭代译码算法［7］

若接收序列总长度（L）大于预先设定的译码长度，则一般将接收序列按译码长度n分成若干组，译码算法一般分为下面几个步骤 ① 获取接收序列的第i（0＜i≤［L／n］）组；② 由该接收序列计算出伴随式；③ 由伴随式计算差错定位多项式的系数；④ 求差错定位多项式的根，找出错误位置；⑤ 进行纠错；⑥ 重复以上步骤直至完成整个接收序列的译码。如何由伴随式计算差错定位多项式的系数是BCH译码中最为复杂、关键的一步，不同的实现方法导致了不同的算法。

2．2 迭代译码算法

在BCH码的代数译码算法中，译码的复杂度和译码的速度往往取决于求σ（x）的根。Massey于1969年提出一种较为简单的算法求解错误位置多项式。在BM算法［3］中，将求解错误位置多项式的问题转化为解线性方程组的问题。

设S为伴随式，S＝ （S1，S2，…，S2t），其中Sk＝R（βk），

则x1，x2，…，xe错误位置

有关键方程

根据关键方程，通过修正逐步求出修正项dj，最终得出σ（2t）（x）。具体迭代步骤如下:

计算得出dj＋1，并以此为基础进行下一步的迭代。

经过2t次迭代即可求出σ（2t）（x）和w（2t）（x）即为σ（x）和w（x）。

2．3 分组查找表译码［6］

BCH是循环码的一个重要子类，同时也是线性分组码的一种，因此线性分组码的查译码表［5］的译码方式同样适合用BCH码。分组查找表译码算法［6］基本步骤与BCH码一般译码算法基本相同，仅针对计算复杂的第二步进行优化，采用查译码表的方式进行译码。因此分组查找表译码算法主要包括:（1）构造伴随式与错误图样对应关系的查找译码表；（2）计算所接收序列中一个分组的伴随式；（3）通过分组查找表找到对应的错误图样，进行译码。其中构造译码表为译码之前一次性构造并且一旦确定BCH码的码字多项式后译码表也唯一确定。

2．4 MapReduce框架

MapReduce是一个用于大数据集并行处理的编程模型，主要由Map（过滤排序）和一个Reduce过程（执行总结操作）组成。

（1）Map过程:接受一个键值对（key－value pairs），产生一组中间键值对，中间键值对由框架传递给Reduce过程。

（2）Reduce过程:接受一个主键及该主键对应的值组将这些值组进行运算，从而合并为一组规模更小的值。

作业执行过程可以简化为:

3 分组并行译码算法原理

查表译码需要构建出所有错误图样与其所对应伴随式组成的译码查找表，将伴随式值的大小作为查找表的索引值。由所接收到的码字可以计算出伴随式，以该伴随式的值作为索引值查找译码表，经过有限次的查找可以很快确定错误图样从而找到错误位置完成接收码字的纠错。与迭代译码算法相比，查表译码方式有着逻辑实现简单、译码速度快、易于分组并行的优点，但要占有较大的存储空间，适合于软件译码的方式。

3．1 构造译码表

生成BCH码的译码表的步骤如下:

（1）求所设计码的生成多项式

如［15，7，5］BCH 码的生成多项式，码以α，α3为根，α3的最小多项式为

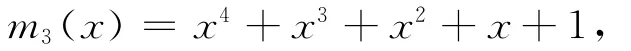
（2）由生成多项式计算得到生成矩阵和校验矩阵，具体有:

这样即可确定伴随矩阵与错误图样之间的关系，经计算可得伴随矩阵与错误图样的对应关系。表1中所列出的为BCH（7，4）的伴随阵与错误图样对照关系表。其中h＊（x）为h（x）的逆多项式

表1 BCH（7，4）的伴随阵与错误图样对照关系

3．2 分组查表译码

在大数据环境中，数据的读取速率往往很高，甚至达到G比特每秒，在大速率的情况下，设计复杂，译码缓慢的迭代译码算法很难处理。根据MapReduce的分片（分组）处理“分而治之”的思想将大数据量的信息按照一定长度进行分组，再利用并行框架［5］进行译码是解决的途径之一，采用 MapReduce框架的并行译码［8］算法如图1所示。

图1 分布式并行BCH码译码原理图

具体步骤如下:

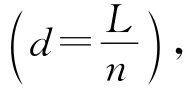
（2）针对每一接收片段Ri（x）（i＝d－1，d－2，…

1），计算伴随式:

（3）若Si（x）＝0（i＝d－1，d－2，…1）则该片段接收序列无误；

（5）将片段码字的估值还原为＾C（x）。

信息串R（x）译码完毕。

4 译码性能对比分析

4．1 译码时间对比

为了验证本文提出的改进算法在译码速度上的优势，采用了MapReduce环境下对40万字节BCH（31，21，5）编码的接收序列进行译码仿真。单机仿真计算机的性能为:Intel®CoreTM双核CPU、2．10GHz主频、2G内存、200G磁盘空间。分布式环境采用4台Intel®CoreTM双核CPU、2．10GHz主频、2G内存、200G磁盘空间的计算机，其中一台计算机作为NameNode和Job－Tracker，其余3台负责具体计算任务。

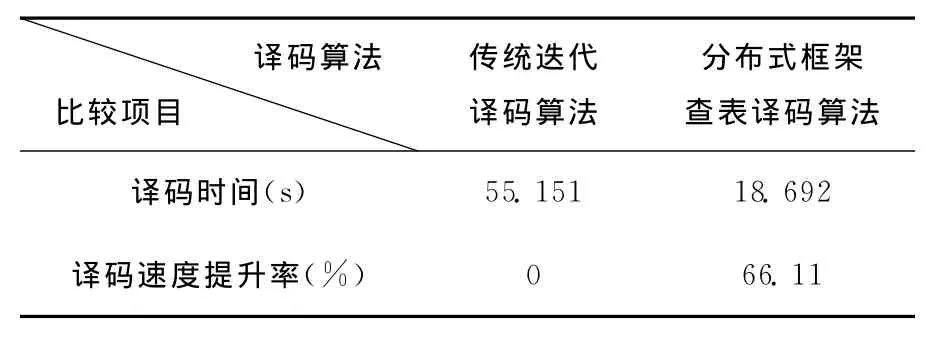
表2 分布式并行查表译码与传统迭代译码时间对比

从表2可以看出，采用本文提出的分布式并行查表译码算法在译码时间上较传统的迭代算法有着较大地提升，译码速率比传统迭代译码算法快66．11%。因此本文提出的分布式并行查表译码算法在译码速度上具有较大的优势。

4．2 计算量对比分析

由于查表译码算法译码前已生成译码表，在译码时无需再计算位置多项式的根，仅需计算伴随式查表即可获得错误图样，从而操作数大大降低。表3给出了迭代译码和查表译码的操作数（左移、右移等位操作）和所占空间资源对比分析。

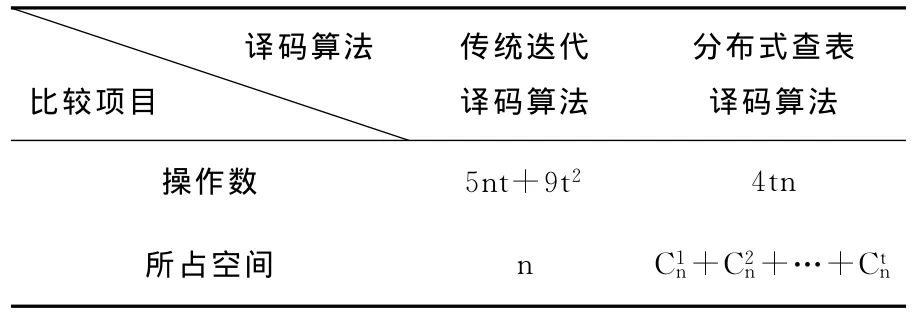
表3 BCH 译码计算量和空间消耗对比表

从表3可以看出，迭代算法操作数随着分组长度t增加操作数显著增加，而查表算法操作数当t的增大时影响较小。传统迭代译码算法所占的存储空间较少，分布式查表译码算法也随着码字的增加需要占用更多的存储空间。

5 结束语

综上所述，BCH码查表并行译码算法充分利用了分组码和BCH码的特点，显著提高了译码的速度、降低了译码计算量。相比较于传统的迭代译码算法，并行查表法有着更好的性能，更适合于大数据环境下的编译码。

由于查表译码算法需要存储伴随式和错误图样的关系组成的查找表，随着码字的增长，译码表将迅速增大从而占用大量的存储空间，在较长码字的情况下，此种算法将不再适用。但考虑到分组码的信息位分组长度t可以根据需要调整大小，因此可以选择适当的长度t来避免过长的码字，从而避免占用过大的存储空间。

1 赵晓群．现代编码理论［M］．武汉:华中科技大学出版社，2008．

2 万哲先．代数和编码［M］．北京:高等教育出版社，2007．

3 Berlekamp，Elwyn R，Factoring Polynomials Over Finite Fields［J］．Bell System Technical Journal，1967，46:1853－1859．

4 Jacques Bughin， Michael Chui，James Manyika，Clouds，big data，and smart assets［EB／OL］．http:／／www．itglobal－services．de／files／100810＿McK ＿Clouds＿big＿data＿and%20smart%20assets．pdf．2010－08－01．

5 孔 挺，宫 芳，方扬扬．基于查找表的BCH码快速译码算法［J］．哈尔滨商业大学学报（自然科学版），2011，27（6）:819－823．

6 Jeffrey Dean，Sanjay Ghemawat．MapReduce:Simplifed Data Processing on Large Clusters［EB／OL］．http:／／research．google．com／archive／map－reduce－osdi04．pdf．2004:1－5．

7 王新梅，肖国镇．纠错码－原理与方法 ［M］．西安:西安电子科技大学出版社，2001．

8 冷芳玲，鲍玉斌．基于MapReduce的数据聚集运算算法［J］．中国科技论文在线，2011，7（7）:469－481．