一种三次多项式湍黏性底边界层的流场分布
2014-12-15纪艳菊刘淑波
纪艳菊 , 刘淑波 齐 震
(1.中国科学院 海洋研究所, 山东 青岛 266071; 2.中国科学院大学, 北京 100049; 3.中国石油大学(华东)理学院, 山东 青岛 266580; 4.河北省地矿局第四水文工程地质大队 沧州市海洋环境监测站, 河北 沧州061000)
湍流底边界层的流场结构对于海洋工程研究具有十分重要的意义和理论价值, 比如泥沙的侵蚀,悬浮沉积过程[1-2]、湍流混合[3]、能量耗散[4]及Ekman抽吸[5]。迄今为止虽然有很多文献从不同角度(如理论上和实验上)研究了底边界层的动力特征[6-13], 但是精确地描述复杂湍流底边界层的动力机制却十分困难。实际海洋中, 有很多因素影响底边界层的动力系统, 如垂向涡黏性的分布、底部粗糙度、底边界层上部流场的分布和Coriolis力等。其中垂直涡黏性的分布是一个十分重要的参数, 对它适当且准确地描述可以更好地预测和模拟湍流底边界层的动力结构。
为了更加准确地理解边界层的动力特征, 垂直涡黏性的各种假设被广泛地提出[9-21]。众所周知, 垂直涡黏性是底边界层高度的函数。例如, 由长度混合假设知, 涡黏性υ1是底边界层高度的线性函数υ1=kzu*, 其中k是 Karman常数(k≈0.4),z是底边界层的垂直高度(原点在底边界层的底部, 向上为正),u*=(τ/ρ)1/2是底摩擦速度,ρ是流体的密度,τ是底剪应力。利用线性参数模式, Weatherly等[9]推导出了海洋倾斜底边界层的速度解析解; Cushman-Roisin等[5]利用该涡黏性研究了深海洋的底部Ekman抽吸; Zou[10]在该模式的基础上, 同时考虑了湍流消耗和扩散效应, 得到了湍流底边界层的速度解析解。另外, Ostendorf[12]和 Prandle[13]利用该线性模式分别研究了考虑地球旋转的湍流底边界层和边界条件为无应力的潮流底边界层。然而, 在这2个研究中, 由于分别考虑了地球的旋转和底边界层上表面应力的消失, 涡黏性的分布需要进一步修正。为了解决这个难题, 各种不同的涡黏性模式被提出。Beach等[14]提出了线性-指数形式的涡黏性υ2,υ2=k1ku*ze xp(-k2z/d), 其中k1,k2为 2个常系数,d是底边界层的有效高度。通过该涡黏性, Hsu等[15]预测的湍流底边界层的速度剖面和实验观测结果一致, Absi[16]计算了细沙和粗泥沙悬浮液的浓度。另外,Myrhaug[17]利用了湍流涡黏度的二次形式υ3=ku*z(1 -z/d)描述了粗糙底边界层的湍流运动。根据实验数据, Nezu等[18]得到了该涡黏性的二次形式,并进一步揭示了底边界层的速度分布。Perlin等[19-20]利用此涡黏性研究了底Ekman层的湍流、分层和速度分布; Shimizu[11]考虑了分层和地转效应得到了湍流底边界层的解析模式, 并且和已知的实验结果拟合良好。李明悝等[21]通过分析不同水深和潮流振幅情况下, 得到了一个潮致垂直混合涡动黏性系数υT的拟合公式υT=L(1 -z)2z2, 其中L为常数, 与潮流振幅和底混合层厚度有关, 在该参数化方案下, 模拟的海洋温度三维结构和实际观测基本吻合。
为了对问题进一步探讨, 在本文研究中, 我们提出了三次多项式形式的涡黏性υ=az2(1 -z/d),其中a是常数(与摩擦速度u*与有效高度d有关),得到了湍流底边界层的速度的解析解, 并进——步得出底边界层内其他的动力参数的解析形式。在数学方法上, 湍流底边界层的流场分布用超几何函数表示[22]。超几何函数在函数的展开和量子力学的问题中有很多的应用[23-24], 在湍流底边界层的动力系统问题中却很少被用到。本文在一个新的湍黏性分布下, 对方程进行适当的变量代换, 最终化简为超几何方程, 利用超几何方程的基本解—超几何函数来表示湍流底边界层的动力结构。在文章最后利用数值结果讨论了底边界层的动力结构受一些参数的影响情况, 为研究底边界层动力结构选用合适的涡黏性的形式提供了借鉴和参考。
1 底边界层的控制方程和解析解
假定湍流底边界层内的流体充分混合, 即密度均匀, 同时边界层底部粗糙平坦。因此湍流底边界层的运动基本方程可以简化为Navier-Stokes (N-S)方程:
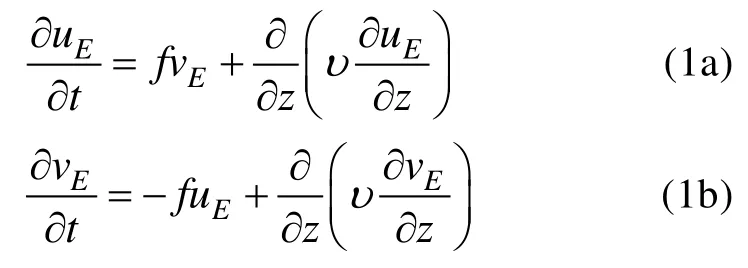
其中f= 2 Ω s inφ是Coriolis参数(本文中假设为正常数), Ω和φ分别是地球自转角速度和地理纬度,t是时间,z是垂直高度(指向上为正的, 零点在底边界层的底部, 见图1)。υ=az2(1 -αz)为动力涡黏性,其中a是常数(与摩擦速度u*和底边界层的有效高度d有关),α=1/d。uE和vE分别为x,y方向的亏损速度(Ekman速度), 它们是z和t的函数。而uI和vI为底边界层上部x,y方向的速度分量(即底边界层的总速度u,v分别为u=uI+uE和v=vI+vE)。
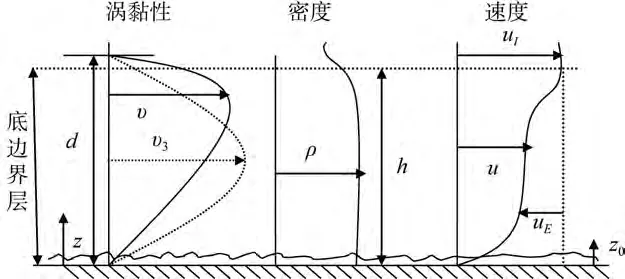
图1 底边界层示意图Fig.1 Bottom boundary layer sketch
方程(1a)和方程(1b)的顶部边界为无应力条件:
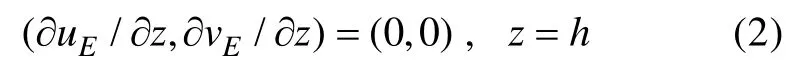
其中h为边界层的厚度。
底边界层的底部边界为无滑移条件:

其中z0为底粗糙度, 本文假定为正常数。
底边界层的上方由海洋潮汐力所产生的内部流场为:

其中ω为内部流的角频率,u~I和v~I为内部流速的复振幅且为常值,c.c.为复共轭。控制方程(1a)、(1b)在边界条件(2)和(3)下, 得到了底边界层速度的解析解。引入两个新的变量F1=vE-iuE和F2=vE+iuE,带入方程(1)得:
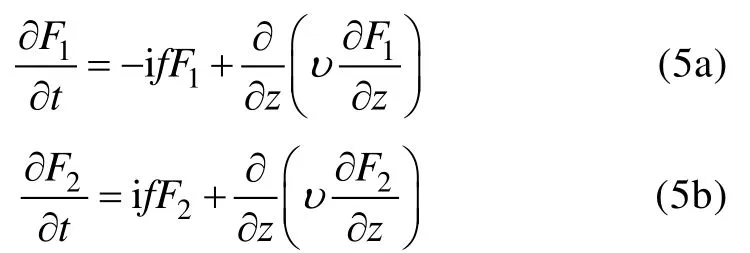
令F1=ρ1(z) eiωt,F2=ρ2(z) eiωt, 其中ρ1和ρ2分别是
z的两个不同的函数, 方程(5)可简化为:
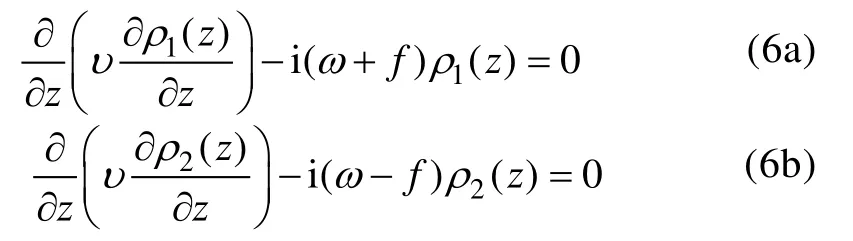
令ρ(z) =rpV(r),r=αz, 其中V是r的函数,p是复
1常数, 将上式代入(6a)。为进一步化简方程的需要,令p2+p- i (ω+f)/α= 0 , 使得方程(6a)可化为超几何方程[22]:
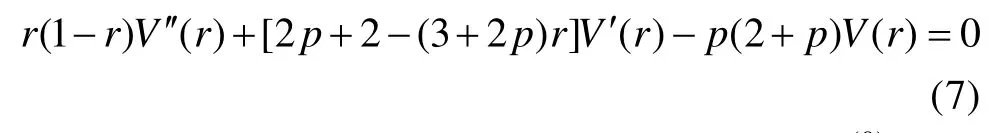
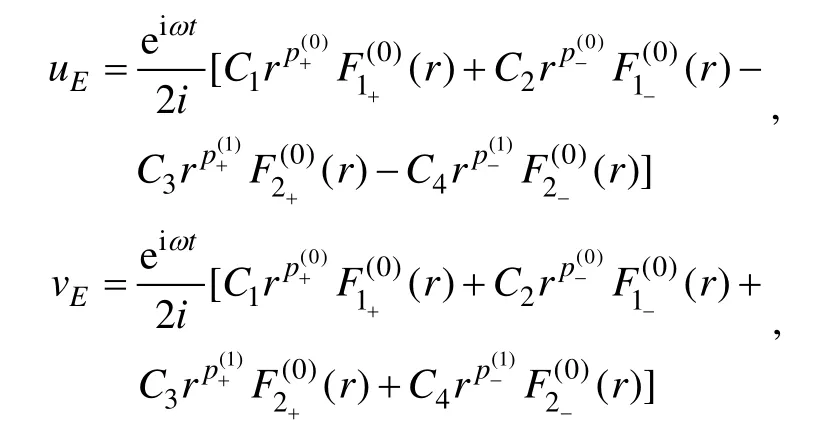
其中C1、C2、C3和C4是待定系数, 可由边界条件(2)和(3)确定。则方程(1a)、方程(1b)的解为

其中

2 底边界层的动力参数
2.1 剪应力
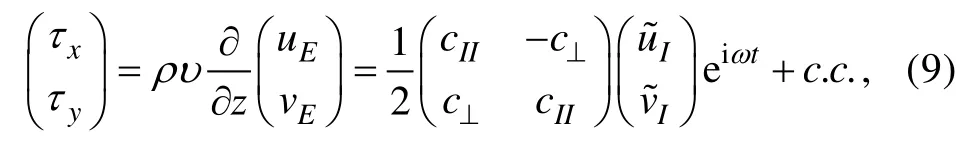
其中cII和c⊥为复线性摩擦系数,
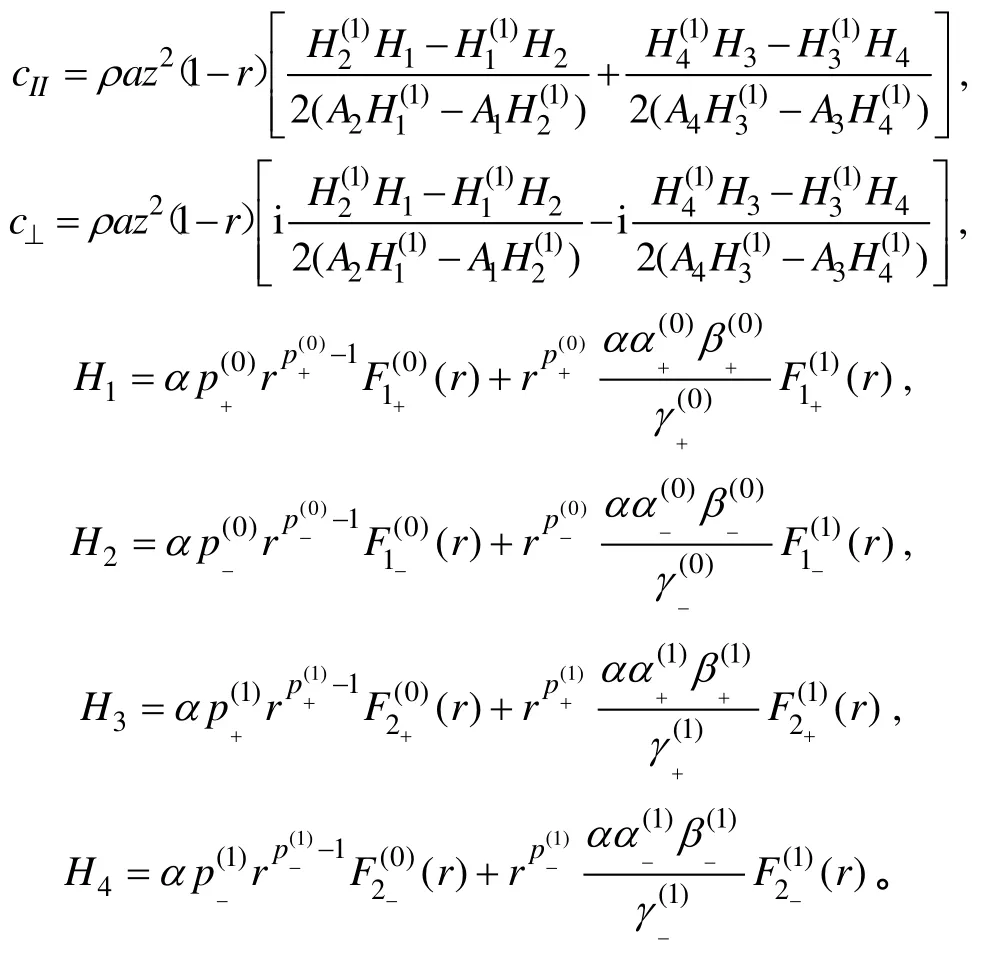
2.2 Ekman传输
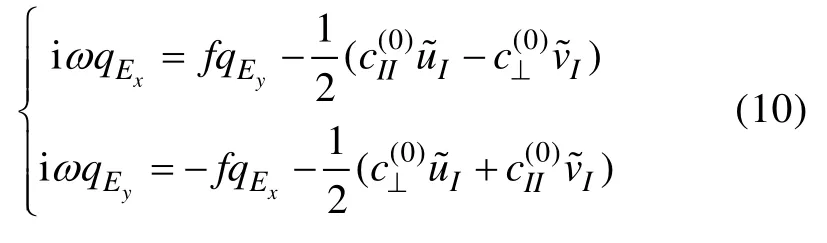
其中
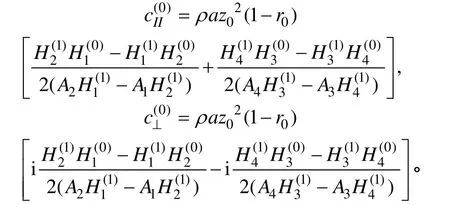
进一步解得

2.3 Ekman抽吸
假设流体为不可压缩的, Ekman抽吸可由对三维 连 续 方 程 ∂u/ ∂x+ ∂v/ ∂y+ ∂w/ ∂z= 0 两 端 分 别 从z=z0到z=h积分并结合公式(11)得到
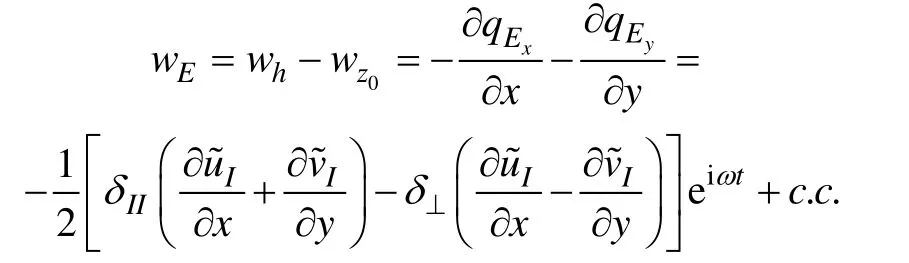
其中wh表示z=h时, 底边界层的垂向速度,wz0表示z=z0时, 底边界层的垂向速度,wE表示Ekman抽吸,在伸展和压缩海洋内部流方面起重要作用。
2.4 底边界层近底部速度和剪应力
接近底边界层的底部, 有极限(α=z/d→ 0 )和rp≈ 0 , 并利用超几何函数的性质,[22]F(α,β,γ, 0 ) ≈ 1 , 利用边界层速度公式(8), 我们得到底边界层的近底部速度剖面,
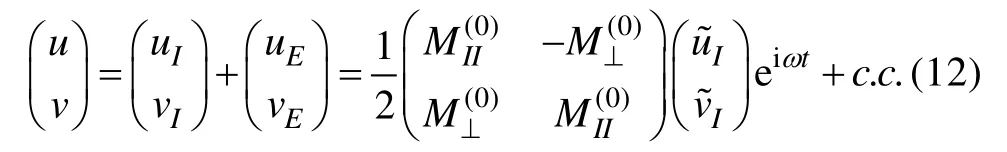
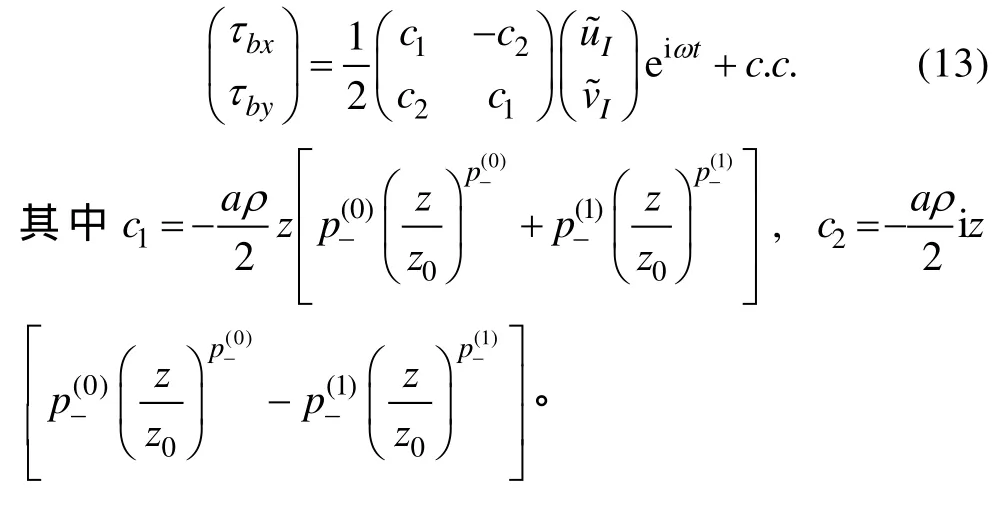
3 数值分析
作为动力特征分析, 在这部分, 我们假设一个单一内部流(uI,vI) = ( 0,1)VI, 其中VI为实常数, 表示速度的大小。在不考虑地转效应的情况下, 分别讨论了平均流的角频率和底边界层顶部粗糙度Δ =1 -h/d(图1)对速度的影响情况(图2和图3)。在考虑了地转效应情况下, 分别讨论了参数S=ω/f和相位角ωt对底边界层速度的影响情况(图4~图6), 以及参数S=ω/f对底边界层剪应力的影响(图7), 更加清晰地理解底边界层内的动力结构。
在t=0s,f=0 rad/s,a=0.1 m/s, (uI,vI) = ( 1,0)VI和VI=1 m/s的情况下, 图2给出了不同的平均流角频率对应的无量纲的总速度剖面(u,v) = (uI+uE,vI+vE)的分布。从图2可以看出总速度的大小|(u,v)|与平均角频率有很大的关系。在底边界层的同一高度上,随着平均角频率的增大而增大, 在角频率为ω= 1.2× 1 0-4rad/s时, 总速度最大, 但是总速度的变化梯度越来越小; 对每个平均流的角频率, 在接近边界层的顶部时, 总速度达到在一个固定值, 在靠近边界层底部, 总速度迅速减小为0。图3给出了不同 Δ =1-h/d对应的总速度分布(=0.1、0.3和0.7)。在底边界层的同一深度, 总速度的大小随着Δ的增加越来越大, 但是影响不明显。特别是在底边界层近底部, 速度剖面对Δ几乎不敏感。
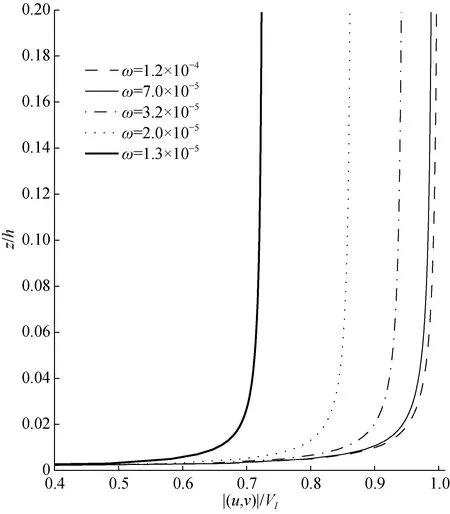
图2 不同的角频率ω下的速度剖面Fig.2 Velocity profile with different angular frequency ω
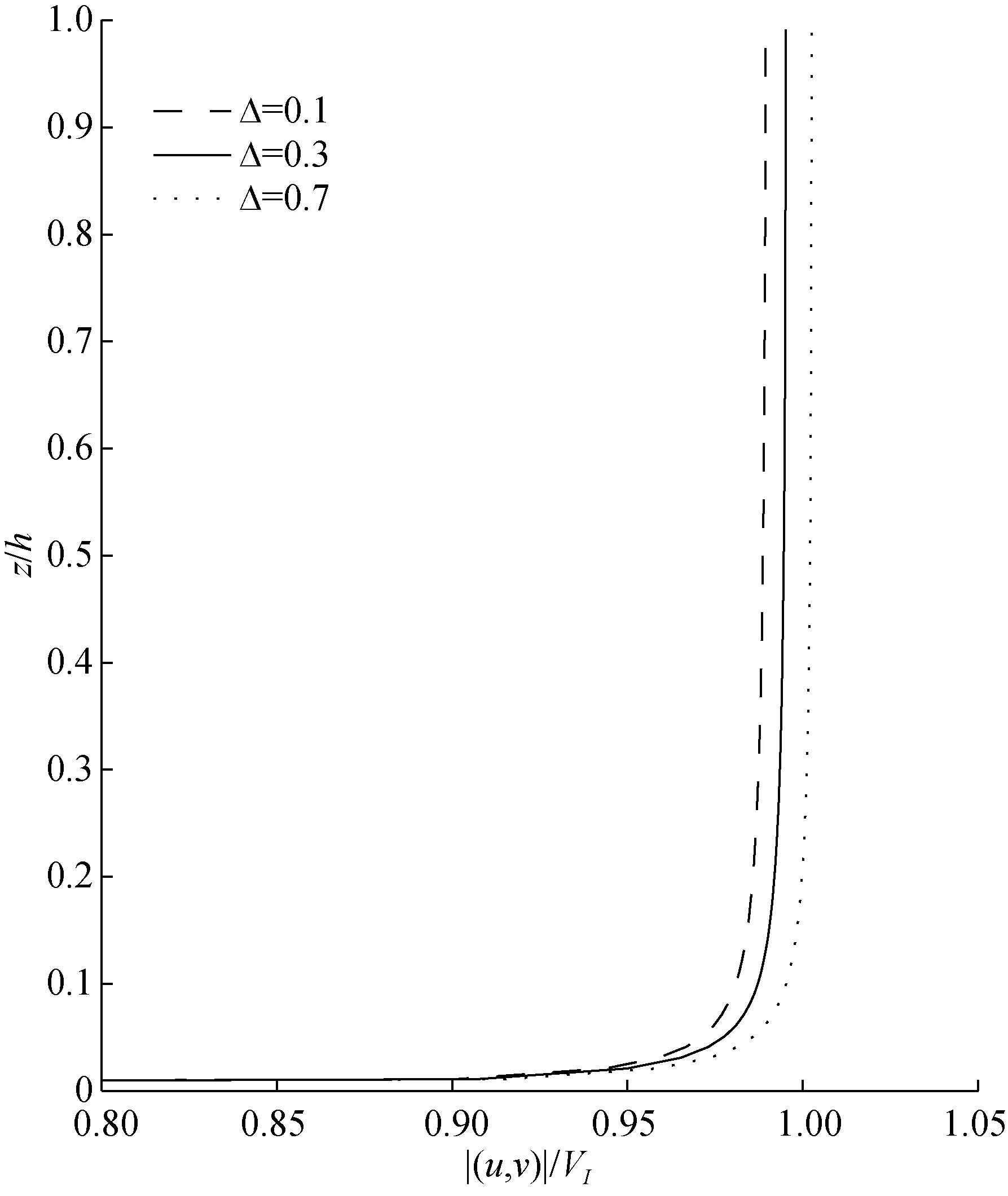
图3 不同的Δ下的速度剖面Fig.3 Velocity profile with different Δ

图4 不同S下的总速度的大小■(u, v)■(a)和相位arg[(u, v)](b)Fig.4 Velocity magnitude ■(u, v)■(a)and phase arg[(u, v)](b) with different parameters S , respectively

图5 在不同S下的亏损速度的大小■(uE, vE)■(a)和相位arg[(uE, vE)](b)Fig.5 Velocity defect magnitude■(uE, vE)■(a)and phase arg[(uE, vE)](b)with different parameters S
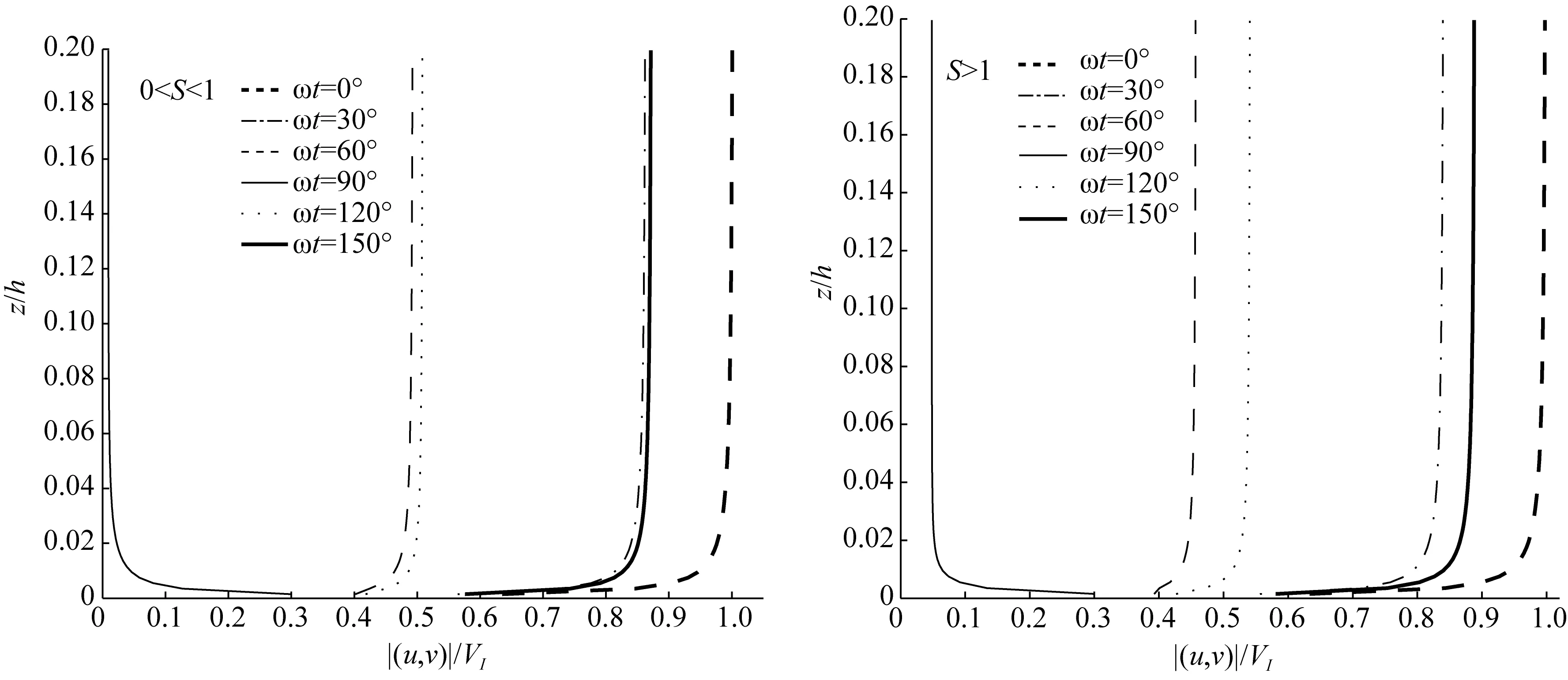
图6 不同相位角tω下的总速度大小■(u, v)■的分布Fig.6 Velocity magnitude profile ■(u, v)■ with different phases tω

图7 不同的S对应的剪应力的大小|(τx , τy ) | (a)和相位arg[(u, v)](b)Fig.7 The shear stress magnitude |(τx , τy ) | (a) and phase arg[(u, v)](b) with different S
在ω=7.27×10-5rad/s,t=0 s,a=0.01 m/s,(uI,vI)= ( 1,0)VI和VI=1 m/s的情况下, 图4给出了在不同的S对应的总速度大小(a)和相位(b)分布(S=0.6、0.9、1.2和2.6)。从图4(a)中可以看出, 速度的大小随着S的变化很小, 特别是在边界层的顶部和底部几乎没有变化。图4(b)可以看出, 速度的偏转角受到地球的自转影响明显, 当 0
在ω=7.27×10-5rad/s,a=0.1 m/s, (uI,vI)=(1,0)VI和VI=1 m/s的情况下, 图6描述了在不同的相位角ωt(ωt=0°、30°、60°、90°、120°和150°)对应的总速度剖面的分布。在边界层内, 当0
在ω=7.27×10-5rad/s,a=0.01 m/s, (uI,vI)=(1,0)VI和VI=1 m/s的情况下, 图7给出了在不同S对应的底边界层的剪应力大小(a)和相位(b)的分布情况。从图中可以看出, 底边界层的剪应力随着高度的减小而增大, 最大值约为 0.14 Pa; 在底边界层的相同高度, 剪应力的大小和相位随着S的增加而减小,在底边界层的底部, 相位约为–25°, 在底边界层的顶部, 最大剪应力的相位约为150°。
4 讨论
通过假定底边界层的涡黏性的三次多项式形式,在简化的N-S方程的基础上, 通过变量代换, 利用超几何方程的性质, 求得了粗糙底边界层的速度的解析解。并进一步得到了底边界层的其他的动力参数,如速度分布, 剪应力, Ekman传输, Ekman抽吸及近底部的速度和剪应力, 并且在该涡黏性模式下得到的近底部的速度非一般的对数形式。利用数值结果分析, 首先在不考虑地转的情况下, 底边界层内的总速度随着平均流的角频率的增加而增加, 而对于底边界层顶部粗糙度的变化却不是很敏感。其次是考虑地转的情况下, 讨论了底边界层内的总速度,亏损速度及其底剪应力的变化, 由于地转因素, 速度及其剪应力都有相位的变化。
本文所假设的涡黏性模式, 从理论上丰富了底边界层涡黏性的形式, 须进一步通过实验结果或观测结果来验证该模式的正确性, 这也是我们下一步要继续研究的内容。另外, 能否通过进一步修改, 找到更接近观测结果的涡黏性形式, 需要通过更多的实测资料来验证。
[1]Gloor M, Wüest A, Münnich M.Benthic boundary mixing and resuspension induced by internal seiches [J].Hydrobiologia, 1994, 284: 59-68.
[2]曹祖德, 王桂芬.波浪掀沙、潮流输沙的数值模拟[J].海洋学报: 中文版, 1993, 15(1): 107-118.
[3]魏皓, 赵亮, 刘广山, 等.浅海底边界动力过程与物质交换研究[J].地球科学进展, 2006, 21(11):1180-1184.
[4]刘志宇, 魏皓.黄海潮流底边界层内湍动能耗散率与底应力的估计[J].自然科学进展, 2007, 17(3):362-369.
[5]Cushman-Roisin B, Malačič V.Bottom ekman pumping with stress-dependent eddy viscosity[J].Journal of Physical Oceanography, 1997, 27(9): 1967-1975.
[6]Sleath J F A.Turbulent oscillatory flow over rough beds[J].Journal of Fluid Mechanics, 1987, 182: 369-409.
[7]Jensen B L, Sumer B M, Fredsøe J.Turbulent oscillatory boundary layers at high Reynolds numbers[J].Journal of Fluid Mechanics, 1989, 206: 265-297.
[8]Hanert E, Deleersnijder E, Blaise S, et al.Capturing the Bottom boundary layer in finite element ocean models[J].Ocean Modelling, 2007, 17(2): 153-162.
[9]Weatherly G L, Martin P J.On the structure and dynamics of the oceanic bottom boundary layer [J].Journal of Physical Oceanography, 1978, 8: 557-570.
[10]Zou Q P.An analytical model of wave Bottom boundary layers incorporating turbulent relaxation and diffusion effects[J].Journal of Physical Oceanography,2002, 32(9): 2441-2456.
[11]Shimizu K.An analytical model of capped turbulent oscillatory Bottom boundary layers[J].Journal of Geophysical Research-oceans, 2010, 115(C0): 3011.
[12]Ostendorf D W.The rotary Bottom boundary layer[J].Journal of Geophysical Research-Ocean, 1984, 89(10):410-461.
[13]Prandle D.The vertical structure of tidal currents [J].GeophysIcal.and Astrophysical Fluid Dynamics, 1982,22: 29-49.
[14]Beach R A, Sternberg R W.Suspended sediment transport in the surf zone: response to cross-shore infragravity motion [J].Marine Geology, 1988, 80:61-79.
[15]Hsu T W, Jan C D.Calibration of Businger-Arya type of eddy viscosity model's parameters[J].Journal of Waterway Port Coastal and Ocean Engineering-Asce,1998, 124(5): 281-284.
[16]Absi R.Concentration profiles for fine and coarse sediments suspended by waves over ripples: An analytical study with the 1-DV gradient diffusion model[J].Advances in Water Resources, 2010, 33(4): 411-418.
[17]Myrhaug D.On a theoretical model of rough turbulent wave boundary layers[J].Ocean Engineering, 1982,9(6): 547-565.
[18]Nezu I, Rodi W.Open-channel flow measurements with a laser Doppler anemometer[J].Journal of Hydraulic Engineering, 1986, 112(5): 335-355.
[19]Perlin A, Moum J N, Klymak J M, et al.A modified law-of-the-wall applied to oceanic Bottom boundary layers[J].Journal of Geophysical Research-oceans,2005, 110(C10): 110.
[20]Perlin A, Moum J N, Klymak J M, et al.Organization of stratification, turbulence, and veering in Bottom Ekman layers[J].Journal of Geophysical Researchoceans, 2007, 112(C5): 112.
[21]李明悝, 侯一筠, 乔方利.潮致垂直涡动黏性系数的参数化[J].自然科学进展, 2006, 16(1): 55-60.
[22]Abramowitz M, Stegun I A.Handbook of Mathematical Functions.With Formulas, Graphs, and Mathematical Tables [M].Washington, DC: National Bureau of Standards, 1964: 555-566.
[23]厚宇德.超几何函数在量子力学上的应用[J].哈尔滨商业大学学报: 自然科学版, 2002, 18(3): 334-335, 329.
[24]朱嘉麟.超几何方程的解在函数展开中的应用[J].计算物理, 1988, 5(4): 455-465.
