一种北斗伪距单点定位的加权最小二乘(WLS)快速算法
2014-12-14李春华蔡成林邓克群徐李冰
李春华,蔡成林,邓克群,徐李冰
(1.桂林电子科技大学信息与通信学院,广西桂林541004;2.桂林电子科技大学电子工程与自动化学院,广西桂林541004;3.桂林电子科技大学计算机科学与工程学院,广西桂林541004)
0 引言
北斗伪距定位分为单点定位(绝对定位)和相对定位,北斗伪距单点定位因其定位速度快、不存在整周模糊度、接收机价格低等优势,被广泛用于车辆、舰船和飞机的导航和监控、地质矿产的勘测、暗礁定位、海洋捕鱼等领域,提高北斗伪距单点定位的精度与速度,对于加速我国北斗产业化步伐将起到非常重要的作用。目前伪距单点定位普遍采用高斯牛顿迭代最小二乘(gauss-newton iterative least squares,GNILS)算法[1-4]。利用 GNILS 算法进行定位解算,如果所取观测站坐标的初始值与真实值具有较大的偏差,迭代次数将会增加,而每次迭代都涉及矩阵相乘和矩阵求逆,所以计算量也随之增加;文献[5-8]针对GNILS算法计算量大的缺点分别提出了几种改进的直接解算定位方法,直接解算(direct calculation,DC)定位方法对于接收机接收的卫星数据要求很高,然而在实际情况中由于卫星运动和信号遮挡等情况,尤其是在城市建筑密集、山高林密的地方,接收机接收到的卫星数据会受到影响,此时直接解算定位方法的定位精度难以满足需求。直接解算定位方法与GNILS算法相比,优点是定位速度快,实时性好,缺点是定位精度不如GNILS算法。本文针对GNILS算法存在对初始值的估计依赖性强,且迭代计算量大的缺点,结合文献[6]提出的DC算法定位解算快和加权最小二乘(weighted least squares,WLS)算法定位精度高的优点,提出一种北斗伪距单点定位的WLS快速(fast weighted least squares,WLSF)算法。通过北斗实测数据验证表明,WLSF算法计算复杂度显著减少,并且定位精度具有较大改善,这对于当前导航定位接收机改进具有较大的参考价值,对于提高伪距单点定位的精度与速度具有重要意义。
1 北斗导航系统伪距单点定位的原理
北斗卫星导航系统伪距单点定位的原理,即通过接收4颗及4颗以上卫星的导航电文与星历数据,利用卫星导航电文与星历数据解算出卫星的位置,再利用卫星与用户的空间几何关系构造方程求解。其基本原理表示为[2]
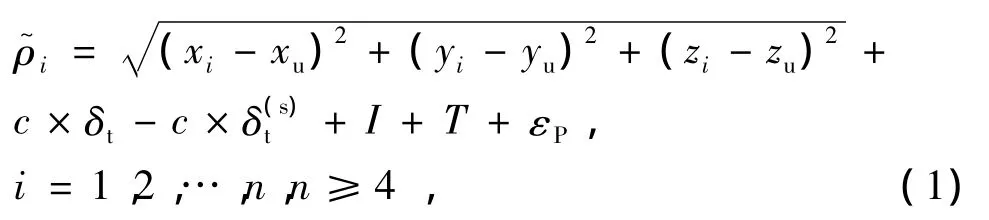
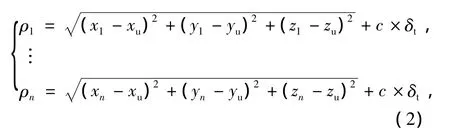
(2)式中,任意 ρi=-(I+T -C × δ(s)t)。
2 DC算法
DC算法是将伪距方程组中相邻的2个方程依次求差,将非线性方程组转化为线性方程组,然后求解。其基本原理如下
将伪距方程组(2)进行移项平方得

在(3)式中依次用后一个方程减去前一个方程,消去未知数的二次项,使得方程组线性化,设R2i=,i=1,2,…,n ,相减后得到n-1个方程,方程组整理后得
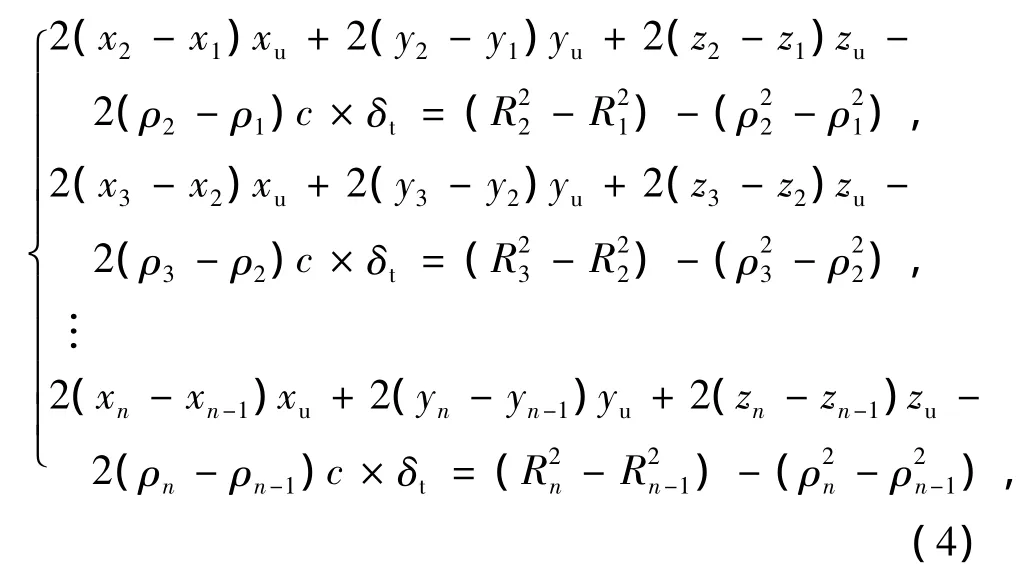
把(4)式写成矩阵形式为

(5)式中
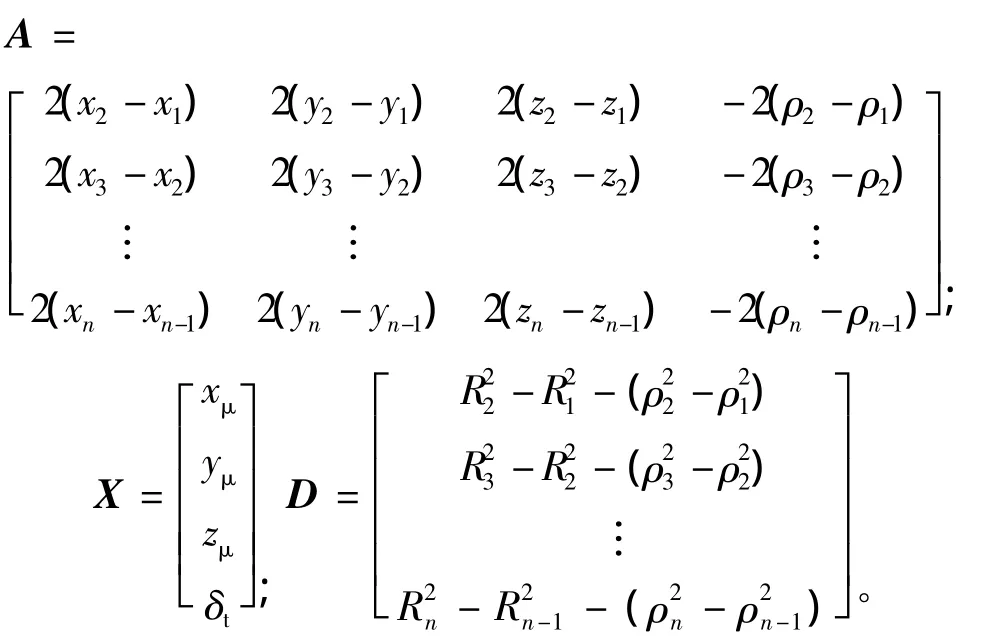
若有n颗卫星,则(4)式只有n-1个方程,显然n>4时可以解算卫星位置。文献[5]提出,即使只有4颗卫星,也能通过直接解算,解算出卫星位置,这里不再赘述。
(5)式中的A矩阵是列满秩矩阵,我们可以利用最小二乘解原理得

在实际计算中发现,当n>5时,方程的系数矩阵ATA的条件数过大,方程是病态方程组,解算出的结果与真实值偏差较大,文献[6]指出,为了解决这个问题,我们在方程组(4)两边同乘以一个系数再将所得的观测方程按最小二乘方法求解,可以得到令人满意的结果。即

(7)式中

因为B矩阵是列满秩矩阵,利用最小二乘解原理得

则接收机坐标(xu,yu,zu)就能由X得出。
3 GNILS算法
GNILS算法是将伪距定位方程中的非线性函数按泰勒级数展开,取至一次项进行近似代替,然后利用线性最小二乘原理求解线性方程的解,逐次迭代,使得线性方程的解逐次逼近非线性方程的解,其基本原理如下。
将(2)式右边的非线性函数按照泰勒级数展开,取至一次项进行线性化,得到的方程形式为
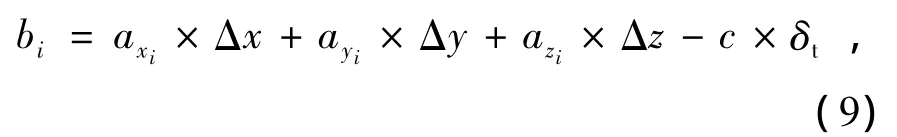
按照最小二乘原理得[6]

(10)式中

求出4 个估计量 Δx,Δy,Δz,c×δt,再更新 X0=(x0,y0,z0,c×δt),令 x0=x0+ Δx,y0=y0+ Δy,z0=z0+Δz,B0=B0+c× δt,重复上述过程进行迭代,直到 Δx,Δy,Δz足够小,即满足

设定一个阈值e,当满足(11)式时,解算出来的值即为用户接收机坐标和接收机钟差,应为xu=x0+ Δx,yu=y0+ Δy,zu=z0+ Δz,B=B0+c×δt。
4 WLSF算法
WLSF算法流程主要分为2个步骤:第1步,利用DC算法求解接收机大概位置坐标;第2步,利用第1步求解的坐标值,将其作为迭代初值,并构造权系数矩阵ω,再根据基于WLS原理的GNILS算法再次求解接收机的位置坐标,具体操作步骤如下。
利用(8)式得到的 X=(x0,y0,z0,B0),取 X0=(x0,y0,z0,0),把 X0=(x0,y0,z0,0)作为 (xu,yu,zu,c× δt)的初始值。
为了利用WLS原理求解接收机坐标,我们构造一个权系数矩阵ω,加权矩阵从(9)式中的bi着手考虑,首先分析一下bi=ri0+c×δt-ρi的组成成分:ri0+c× δt=c×δt为线性化点相对应的伪距值,ρi=是指第i颗卫星与用户实际位置相对应的无误差伪距值,那么bi是指第i颗卫星与接收机实际位置相对应的无误差伪距值与线性化点的相对应伪距值之间的偏差,如果bi越大,则这颗卫星在定位解算中占的比重应当越小,才能提高定位精度。基于这一思想,我们可以构造权系数矩阵ω,令,即为第i颗卫星与用户实际位置相对应的无误差伪距值和与线性化点相对应的伪距值之间的偏差的均值,第RMS颗卫星的bi与相差越大,则此卫星在定位卫星比重中占的比重越少,所以权系数矩阵可以构造为

按照加权最小二乘原理得[6]

同样求出 4 个估计量 Δx,Δy,Δz,c× δt,再更新X0=(x0,y0,z0,c× δt),令 x0=x0+ Δx ,y0=y0+Δy,z0=z0+Δz,B0=B0+c×δt,重复上述过程进行迭代,直到 Δx,Δy,Δz足够小,即满足
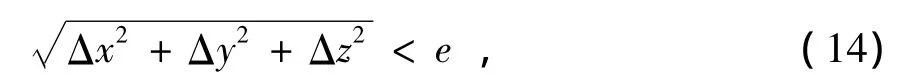
设定一个阈值e,当满足(14)式时,解算出来的值即为用户接收机坐标和接收机钟差,应为xu=x0+ Δx,yu=y0+ Δy,zu=z0+ Δz,B=B0+c×δt。
5 算例分析
为了验证WLSF算法的优越性,利用实验室和芯星通UB240-CORS-ⅡBD2/GPS双系统四频高精度接收机采集了从2013年8月4日至10日的北斗卫星数据。在进行算法验证之前,接收机天线相位中心位置采用Novatel双频载波相位接收机和滞后IGS精密星历,利用3天的观测数据根据GPS精密单点定位(precise point positioning,PPP)算法进行测定,测定的接收机天线相位中心位置坐标为 (-2 005 191.254 5,5 411 087.495 6,2 707 880.732 4),PPP 算法解算出来的接收机位置坐标精度能达到厘米级。
从2013年8月6日中任意提取某一历元时刻卫星数据,首先根据导航电文和星历观测文件,利用地球同步轨道(geosynchronous earth orbit,GEO)和倾斜地球同步轨道(inclined geosynchronous orbits,IGSO)/中地球轨道(medium earth orbit,MEO)卫星的卫星位置解算算法得出卫星的地心地固(earth centered earth fixed,ECEF)坐标,并利用对流层延迟改正模型算法、相对论误差改正算法、地球自转改正算法、电离层延迟改正等算法对每颗卫星的伪距进行修正,将其列于表1,然后利用卫星位置坐标、修正后的伪距,分别采用GNILS算法、DC算法与本文提出的WLSF算法求解接收机坐标,将求解结果与由GPS的PPP算法解算出来的接收机位置坐标(-2 005 191.254 5,5 411 087.495 6,2 707 880.732 4)进行比较,将比较结果列于表2,并用图1直观地表示出来。表2中,(ΔX,ΔY,ΔZ)指通过上述3种定位算法解算出的接收机在ECEF坐标系中的坐标与PPP算法解算出来的接收机位置坐标的差值,RMS=,Δδ=c×δt,分别统计GNILS算法、DC算法、WLSF算法3种定位算法的计算量,结果如表3所示,其中,n为卫星颗数,m为迭代次数。

表1 某一观测历元时刻BD卫星坐标和伪距修正值Tab.1 BD satellite coordinates and revised pseudo-range at one epoch time
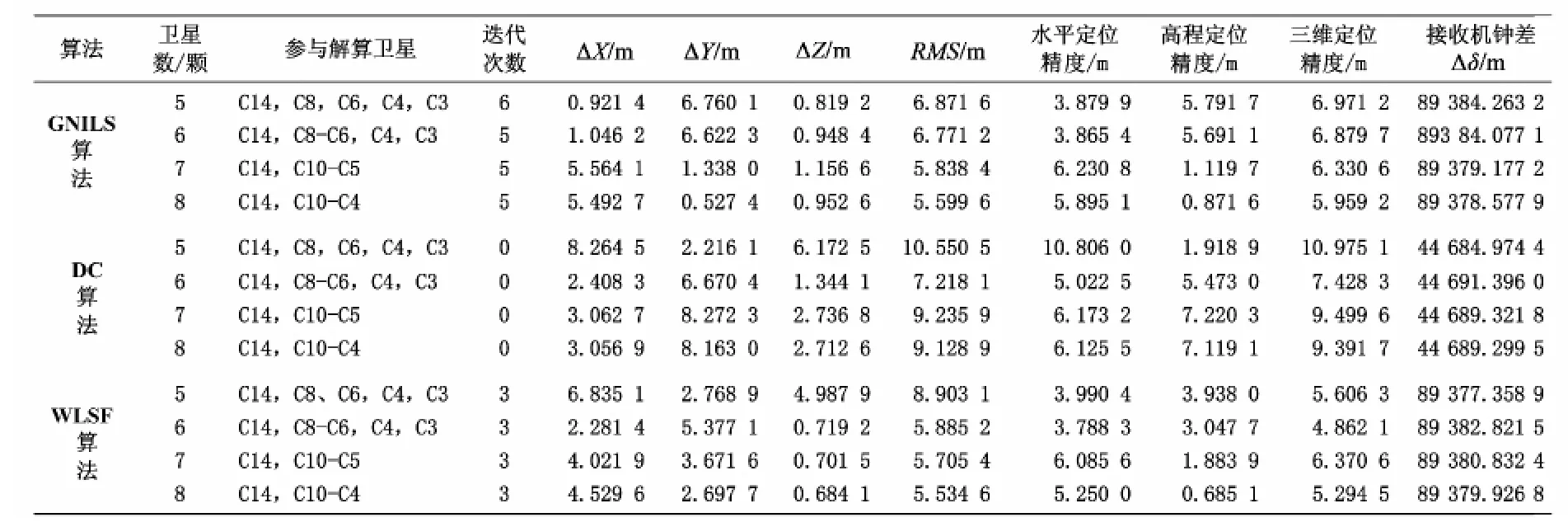
表2 3种定位算法定位结果比较Tab.2 Positioning results comparison for three positioning algorithms

表3 3种定位算法计算量比较Tab.3 Calculated quantity comparison for the three positioning algorithms
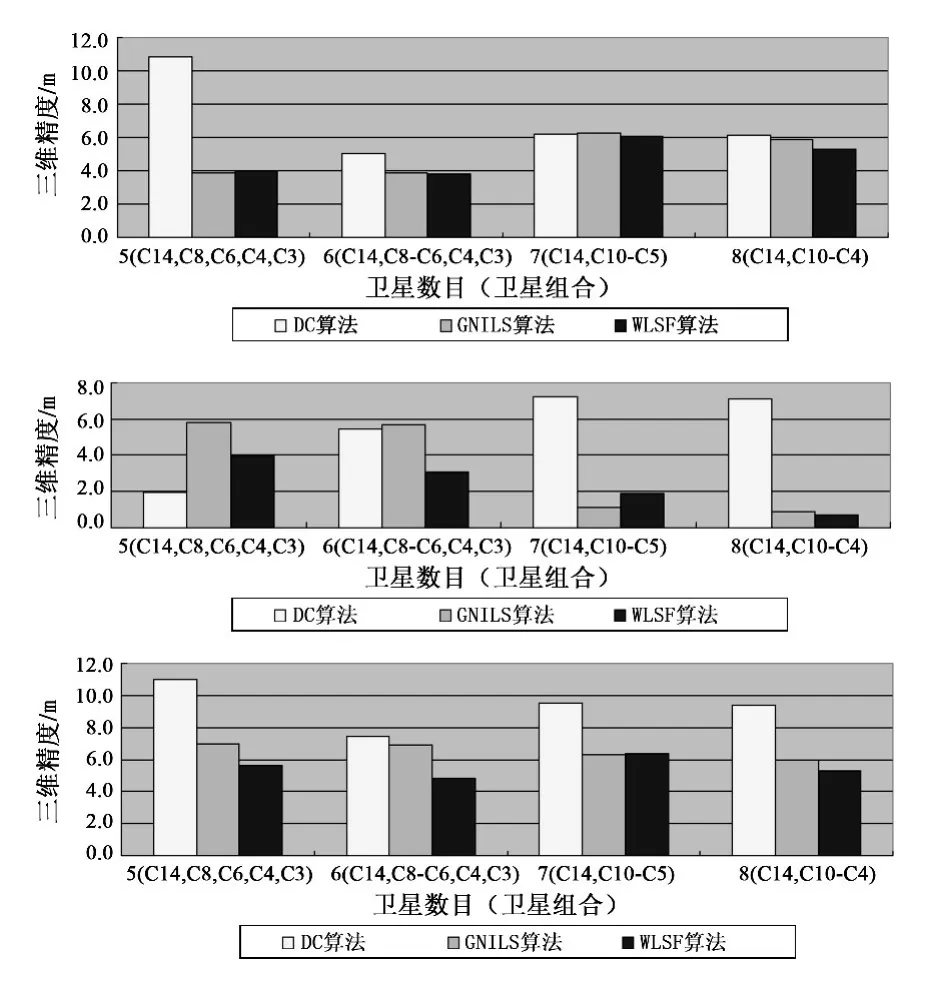
图1 不同卫星数目、不同卫星组合下3种算法的定位精度比较Fig.1 Positioning results comparison for three algorithms under the different number and combinations of satellites
从图1、表2可知,WLSF算法的定位精度比GN算法和DC算法的定位精度都要高,且DC算法定位精度最差。6颗卫星的定位精度大于5颗卫星的定位精度,8颗卫星的定位精度大于7颗卫星的定位精度,说明定位精度与卫星数目有关,而图1中7颗卫星的定位精度没有6颗卫星定位精度好,是因为参与解算的卫星组合不同,这说明定位精度还与卫星的空间几何分布有关。
从表2和表3可以得出以下结论。
1)GNILS算法的定位精度非常高,但迭代次数多,计算量大,随着卫星数目增加,定位精度提高。
2)WLSF算法相比GNILS算法,虽然多了利用DC算法计算迭代初值这一步,但它使得迭代次数减少,计算量总体来说比GNILS迭代定位算法小,且提高了定位精度;WLSF算法相比DC算法,计算量虽然增加,但其定位精度明显增加。
为了进一步验证改进算法的优越性,对接收机连续7天接收的数据,每天每隔30 s进行采样,24 h总共2 880个历元时刻,利用导航电文与观测文件解算卫星位置,针对北斗的B1频点,采用klobuchar模型修正电离层延迟[9],saastamoinen 模型、Niell映射函数修正对流层延迟[10-11]等,达到修正伪距的目的,分别采用GNILS算法、DC算法与本文提出的WLSF算法进行处理,将求解结果用无迹卡尔曼滤波方法(UKF)处理后,得出用户接收机在B1频点的水平、高程、三维定位精度,如图2、图3所示。利用北斗的B1和B2频点,采用双频改正法修正电离延迟[12],继续比较GNILS算法与WLSF算法的处理结果,如图3所示,由于每一天相同算法处理结果的优劣情况相同,这里只给出2013年8月4日的实验处理结果如图2—图4所示。
从图2、图3看出,DC算法的高程定位精度极不稳定,会产生很大波动,这是因为一旦接收的某些卫星的数据有问题,采用直接解算方法将会直接影响定位结果,而GNILS算法和WLSF算法都有迭代过程,使得定位精度相对稳定,由图3、图4可以看出,WLSF算法的定位精度明显高于GNILS算法,这是因为实验室接收机每个历元时刻能接收8颗以上北斗卫星,这与表2结果相符,也进一步说明WLSF快速定位算法能够提高定位精度。

图2 B1频点3种算法的定位结果比较Fig.2 Positioning results comparison for three algorithms at B1frequency
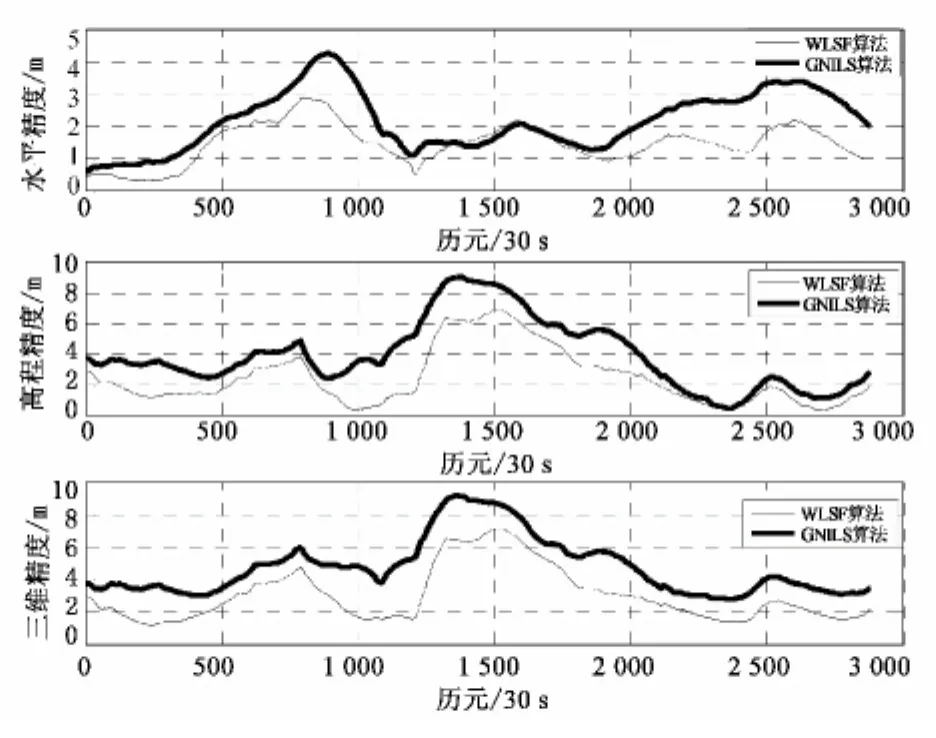
图3 B1频点WLSF算法与GNILS算法的定位结果比较Fig.3 Positioning results comparison between WLSF algorithm and GNILS algorithm at B1frequency
6 结束语

图4 B1+B2频点WLSF算法与GNILS算法的定位结果比较Fig.4 Positioning results comparison between WLSF algorithm and GNILS algorithm at B1+B2frequencies
WLSF算法利用了DC算法计算速度快的优点,利用它快速算出接收机的大概位置,将其作为迭代初值,减少了迭代次数,克服了GN算法对初始值依赖性高、迭代次数多、计算量大的缺点,同时提出一种新的加权方法,使定位精度明显提高。通过将其运用到北斗导航系统中,分别取单个观测历元时刻的卫星数据与一周的卫星数据,进行仿真计算,验证这种WLSF算法的优越性,这对于当前导航定位接收机的改进具有较大的参考价值,对于提高伪距单点定位的精度与速度具有重要意义。
[1]EI Naggar Aly M.An alternative methodology for the mathematical treatment of GPS positioning[J].Alexandria Engineering Journal,2011,50(4):361-365.
[2]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:61-65,96-106.XIE Gang.Principles of GPS and Receiver Design[M].Beijing:Publishing House of Electronics Industry,2009:61-65,96-106.
[3]KAPLAN Elliott D,HEGARTY Christopher J.GPS 原理与应用[M].寇艳红,译.北京:电子工业出版社,2007:36-42.KAPLAN Elliott D,HEGARTY Christopher J.Understanding GPS:Principles and Applications,Second Edition[M].KOU Yanhong,ranslation.Beijing:Publishing house of Electronic Industry,2007:36-42.
[4]刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2003:103-109.LIU Jiyu.Satellite Navigation and Positioning Theory and Method of GPS[M].Beijing:Publishing House of Science,2003:103-109.
[5]陈丽,吴仁彪,胡铁乔,等.一种新的GNSS快速定位算法[J].信号处理,2012,28(4):514-518.CHEN Li,WU Renbiao,HU Tieqiao,et al.A Novel Fast GNSS Positioning Algorithm [J].Signal Processing,2012,28(4):514-518.
[6]郭秋英,胡振琪.GPS测码伪距绝对定位的几种算法[J].测绘科学,2005,30(5):26-27.GUO Qiuying,HU Zhengqi.Serveral algorithms about GPS measured code pseudo-range absolute positioning[J].Science of Surveying and Mapping,2005,30(5):26-27.
[7]段宇鹏,魏宗康,刘建波.一种GPS最优选星及伪距定位方法[J].中国惯性技术学报,2011.21(2):209-213.DUAN Yupeng,WEI Zongkang,LIU Jianbo.Optimal constellation selecting and pseudo-range positioning algorithm in GPS[J].Journal of Chinese Inertial Technology,2011,21(2):209-213.
[8]田安红,付承彪,赵珊.一种改进的GPS测码伪距单点定位算法[J].重庆邮电大学学报:自然科学版,2009,21(6):736-740.TIAN Anhong,FU Chengbiao,ZHAO Shan.An improved algorithm for single point position of GPS[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2009,21(6):736-740.
[9]张勇,张斌,马能武.单频GPS接收机的电离层延迟改正模型研究[J].大地测量与地球动力学,2012,32(2):69-73.ZHANG Yong,ZHANG Bin,MA Nengwu.On models of Ionospheric delay correction for single-frequency GPS receiver[J].Journal of Geodesy and Geodynamics,2012,32(2):69-73.
[10]QU Weijing,ZHU Wenyao,SONG S L,et al.Evaluation of the Precision of Three Tropospheric Delay Correction Models[J].Chinese Astronomy and Astrophysics,2008,32(4):429-438.
[11]王利杰,李思敏,蔡成林,等.基于不同高度角的对流层延迟改正模型选择[J].测绘通报,2013,(8):10-13.WANG Lijie,LI Simin,CAI Chenglin,et al.Troposphere delay correction model selection based on different altitude angle[J].Bulletin of Surveying and Mapping,2013,(8):10-13.
[12]余明,郭际明,过静珺.GPS电离层延迟Klobuchar模型与双频数据解算值比较与分析[J].测绘通报,2004,(6):5-8.YU Ming,GUO Jiming,GUO Jingjun.Ionospheric Delay Values from Klobuchar Model and Dual Frequency Measurements:Comparison and Analysis[J].Bulletin of Surveying and Mapping,2004,(6):5-8.
