工程牵引车传动系统参数优化仿真分析

2014-12-14张晓亮王金伟

重庆理工大学学报(自然科学) 2014年9期

张晓亮，于英，王金伟

(江苏大学汽车与交通工程学院，江苏镇江 212013)

车辆动力传动系统匹配的好坏与整车动力性、燃油经济性息息相关，也是人们普遍关心和研究的重要问题之一。在车辆开发过程初期，一般基于目标设计要求和已有发动机类型参数等选择传动系参数。当目标车辆的整车质量、质量分配和轮胎等为已知时，传统的合理选择发动机与传动系统的做法是进行大量的试验和动力计算。由于受计算误差、模型精确度以及细节参数简化等条件的限制，结果往往不尽如人意。但计算机通过模拟计算可以较好地解决这个难题。建立整车模型及接近真实的行驶工况条件，可以较好地优化计算传动系统的主要部件，并且得到良好的优化效果。一般可以对发动机、各个挡位速比和主减速比进行优化计算。

1 工程牵引车传动系的建模

图1为工程牵引车传动系统简图。工程牵引车的传动方式为机械液力传动，变速器采用了动力换挡变速系统。动力经传动轴传给液力变矩器，液力变矩器再将动力经由变速器传递给驱动桥，由主减速器和轮边减速器完成减速增扭之后将动力传递给驱动轮。

应用AVL CRUISE提供的模块库，根据整车传动系统简图(图1)，依次从各个子模块库中的相关模块拖入建模工作界面，然后进行物理连接和信号连接。图2为搭建的整车系统模型［1］。

图1 工程牵引车传动系统简图

图2 整车系统模型

2 传动系参数优化方法

近几年计算科学和网络的进步使许多工程领域都引入了优化设计思想，应用最广泛的优化方法有3种:传统优化设计方法、模糊优化设计方法、区间优化设计方法［2］。

任何方法都具有两面性，只有合理匹配模型与优化方法之间的关系才能使优化结果达到最佳［3-4］。根据以上分析，本文建立了动力性和燃油经济性双目标函数，并利用加权组合法将双目标化为单目标，搭建单一目标函数的优化模型［5］。

2.1 选定设计变量

当整车动力传动系统其他组成部分既定或者已知时，传动系统的总传动比是决定车辆动力性与燃油经济性的最后参数。因此，本文选定的设计变量为整车动力传动系的总传动比，即各挡位传动比与驱动桥传动比的乘积值，本优化模型的设计变量为

式(1)中:igj为第j挡速比;i0为驱动桥传动比。

2.2 建立目标函数

最优化设计是在规定的各种设计限制条件下优选设计参数，使某项或者几项设计指标获得最优值。根据特定问题所追求的目标，倘若可以针对该目标建立函数关系，则应用设计变量搭建所需的数学函数关系式，此即为目标函数。对于多变量的最优化问题，目标函数为

本文建立了动力性分目标函数和经济性分目标函数，并将两个分目标通过线性加权组合转换成单一的目标函数，建立传动系统参数优化的数学模型［6］。

1)动力性分目标函数。本文评价车辆动力性能时采用热启动起步连续换挡加速时间，并基于此建立分目标函数，如式(3)所示。

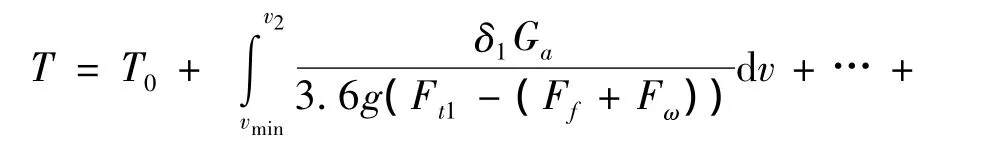
2)经济性分目标函数。车辆燃油经济性采用多工况循环行驶百公里燃油消耗量进行综合评价。本文目标车辆的行驶工作循环工况包含了等速、加速、减速和怠速工况的百公里燃油消耗量(L/100 km)。基于此的经济性分目标函数为

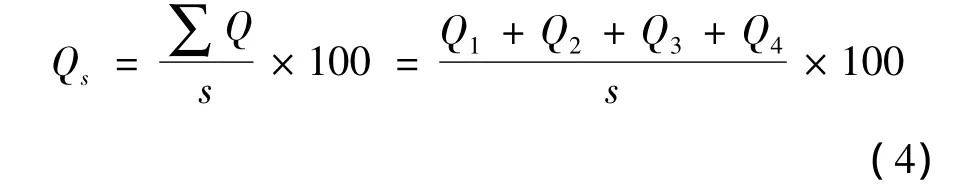
式(4)中:s为行驶距离(m);Q1，Q2，Q3，Q4分别为等速、加速、减速、怠速停车过程的燃油消耗量(mL)。

3)综合目标函数。通过上文的分目标函数线性加权组合得到综合目标函数

式(5)中:r1，r2分别为动力性、经济性加权因子。

本文优化分析研究建立在满足项目对整车动力性提高要求的基础上，因此应尽量提高其燃油经济性，减小百公里油耗，故优化加权因子r1=0，r2=1。

2.3 确定约束条件

工程牵引车在日常使用中对燃油经济性与排放性能的要求建立在满足一定的动力性能要求的基础上。因此，本文对影响动力性的要素(最大车速、爬坡能力、加速能力和速比分配规律)进行讨论，对综合目标函数设立约束条件。

1)最大车速约束。根据车辆的最大车速和发动机最大转速确定总传动比的上限:

式(6)中:igi为最大车速下的挡位数;i0为驱动桥传动比;vmax为最大车速(km/h);nmax为最大转速(r/min)。

根据车辆最大车速下的行驶阻力和发动机最高转速下的输出转矩确定速比的下限:

式(7)中:Fumax为最大车速下的行驶阻力(N);Tumax为最大转速下的输出转矩(N·m)。

2)最大爬坡度约束。传动比的下限根据车辆在最大爬坡度行驶时发动机的最大输出扭矩和行驶阻力确定:

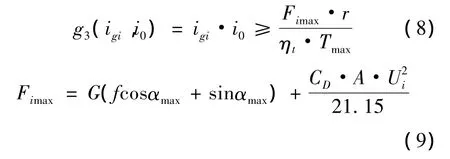
式(8)和(9)中:Fimax为行驶阻力(N);Tmax为最大转矩(N·m);Ui为车速(N)。

3)动力因数约束。为了满足最高挡动力性要求，则需要满足:

式(10)和(11)中:va为当汽车处于最高挡时对应于nT时的车速。

4)速比分配规律约束。一般工程牵引车变速器相邻两挡比值为1.4～2.0左右，且

3 应用实例

应用Matlab优化工具箱中的优化函数，基于本文的设计变量、综合目标函数和约束条件编制执行程序、目标函数M文件和约束条件M文件，从而优化传动系传动比。优化前后各挡传动比及驱动桥传动比如表1所示。

将优化后的传动比参数代入所建立的整车动力传动系统仿真模型中，仿真计算整车动力性和经济性在优化前后的变化，验证优化的合理性和正确性。

3.1 最高车速仿真

优化后，在最高挡6挡时最高车速为71.75 km/h，优化前后相差2.92%，优化后有一定的增加。优化前后各挡最高车速对比如表2所示。

3.2 最大爬坡度仿真

优化后牵引车各挡爬坡度仿真结果输出数据对比如图3所示。优化后1挡的最大爬坡度为66.10%，此时的车速为3.30 km/h，与原车相比各挡位的最大爬坡度大多有所降低。车辆在3、4挡行驶时，最大爬坡度较原车有微小的变化，说明优化后车辆在中高速行驶时的坡度适应性较好。

表1 各挡位传动比

表2 优化前后各挡最高车速

图3 优化前后各挡位爬坡度仿真结果对比

3.3 加速性能仿真

图4为优化前后车辆各挡位加速度对比曲线。由图4可知，优化前后车辆各挡的加速度都有一定的下降，说明整车的加速性能有一定的降低。图5为优化前后各挡最大加速度仿真计算输出数据。

图6为优化前后原地起步连续换挡加速曲线。图6中各曲线分别为加速度曲线、车速曲线和行驶距离曲线;红色表示优化前的曲线，蓝色表示优化后的曲线。图6中:［1］为车辆加速度曲线;［2］车辆车速曲线;［3］为随时间的行驶距离曲线。车辆优化后，车辆的加速时间和行驶距离增加，整车的动力性稍有降低。

图4 各挡位加速度曲线对比

图5 优化前后各挡位最大加速度对比

图6 原地起步连续换挡加速曲线对比

图7为优化前后从30 km/h加速到60 km/h的加速过程曲线，图中各曲线分别为加速度曲线、车速曲线、挡位和行驶距离曲线。［1］表示优化前的曲线，［2］表示优化后的曲线。由图7可知:车辆优化后，车辆在5挡行驶过程中的平均加速度增大，所以车辆在中高速阶段的动力性较优化前有一定的增强。

图7 30～60 km/h加速过程曲线

3.4 循环工况仿真

图8为优化前后UDC循环工况中瞬时燃油消耗对比曲线。图9为工程牵引车在UDC循环工况下车辆怠速、加速、减速、稳态行驶下燃油消耗量优化前后的对比曲线，其中:［1］为优化前;［2］为优化后。

图8 循环工况瞬时燃油消耗对比

图9 不同工况燃油消耗量对比

从优化前后仿真结果输出文件可得:优化后的循环工况油耗为23.40 L/100 km，降低了1.02 L/100 km，改善了牵引车的经济性能。

3.5 稳态行驶工况仿真

稳态行驶工况下不同挡位和车速的燃油消耗量优化前后的对比如表3所示。从表3可以看出:优化后最高挡位稳态行驶的燃油消耗量都较优化前有所降低，车辆总体的燃油经济性得到了提高。

表3 最高挡等速百公里燃油消耗量对比L/100 km

3.6 优化前后整车性能对比

表4为优化前后整车性能对照表。由表4可知:在动力性方面，优化后最高车速提高了2.92%，最大爬坡度下降了3.15%，加速时间延长了，动力性有少量下降。这是因为本文的优化建立在满足动力性要求的基础上，倾向于经济性优化的要求;在经济性方面，车辆循环工况的油耗降低了4.17%，达到了优化的目的，优化效果良好。由此可见，利用所建立的模型对原车动力传动系统进行优化设计取得了较显著的效果。