基于CMMI的企业软件外包风险管理研究

陈 通，刘 彬

(天津大学管理与经济学部，天津 300072)

彼得·德鲁克曾指出:“任何企业中仅做后台支持而不创造营业额的工作都应该外包出去，任何不提供向高级发展机会的活动与业务也应该采取外包形式。”［1］随着信息技术的高速发展和经济全球化进程的加快，企业管理对软件信息系统的需求依赖也随之增强。为了更专注于核心竞争力，企业越来越倾向于将软件信息系统部分或全部外包出去，从而以较低的成本获得更具专业性的软件信息服务。国际著名IT咨询公司IDC最新数据显示，中国软件外包业近10年来发展迅猛，2008—2013年间，中国离岸软件外包收入复合增长率为23%，2013年中国软件外包收入达60.5亿美元。IDC预测，中国软件外包市场将以22.3%的复合年均增长率继续增长，到2017年达到138亿美元的市场规模［2］。

软件外包产业的发展，可以为加快我国新型工业化进程和解决就业等问题提供极大的帮助。但由于软件外包项目在生命周期中存在着各类风险，因此如何有效规避风险是软件外包产业持续健康发展面临的现实挑战。显然，完善软件外包全过程的风险管理，对促进我国软件外包产业的科学发展尤为重要。本文在已有软件外包风险管理研究理论的基础上，创新性地将CMMI能力成熟度模型集成和结构方程模型应用到软件外包全过程风险管理研究中，在“软件外包委托-代理”博弈的最优期望效用条件下，从发包企业的角度出发，对企业如何做好软件外包风险管理工作进行探索研究，以期对企业软件外包风险管理提供参考借鉴。

1 委托-代理下的软件外包博弈最优期望效用条件

企业将软件研发活动外包给软件研发公司，这个过程可以从博弈的角度进行条件分析和优化。发包企业作为软件外包过程的业主单位，可视为博弈的委托方;接包的软件研发公司为业主单位进行软件设计开发活动，可视为博弈中的代理一方。

设定M表示软件代理公司所有可能选择的行动集合，m是其某个选择的行动。函数p(h(x)-j(m))表示软件代理公司的效用，其中x表示发包委托企业可观测的结果，h(x)是发包委托企业制定的激励合同，j(m)表示软件代理公司选择行动m时付出的成本代价。φ表示软件外包过程中的外生变量，Φ是其取值范围，φ的分布函数为F(φ)。设定发包委托企业的效用函数为q(Ψ-h(x))，其中 Ψ(m，φ)是由 m，φ 共同决定的可观测软件效果，Ψ是m和φ的严格递增函数，即软件代理公司工作越努力，软件效果越优秀。

根据以上条件，发包委托企业的期望效用函数为

当发包企业最大化自身的期望效用时，软件代理公司会对发包企业的决策有相应影响。

首先，软件代理公司从接受外包合同中取得的期望效用不能低于其在不接受外包任务时所能得到的最大期望效用。当软件代理公司不接受外包任务时，其所能得到的最大期望效用由市场提供的其他机会决定，记为。因而得到约束条件:

其次，当发包委托企业对软件代理公司的行动m和自然状态φ不能进行有效观测时，软件代理公司总会选择能够最大化自身期望效用的行动m。这时发包企业最希望软件代理公司采取的行动m只能经过软件代理公司的效用最大化原则筛选之后再取得。假定m*是发包企业最希望的行动，m'∈M为软件代理公司可选择的行动范围。软件代理公司选择行动m*的前提是其从选择行动m*中取得的期望效用高于从m'中取得的期望效用，因而得到约束条件:

综上所述，在委托-代理博弈视角下，为了最大化自身的期望效用，发包企业需要制定合适的激励合同来满足约束条件(1)和(2)，促使软件代理公司能够从自身利益出发选择对发包企业最为有利的承包行动策略。

2 CMMI风险管理体系

企业进行风险管理旨在标识潜在问题，从而规划整个生命周期中的风险处理活动，并采取必要措施消除妨碍组织目标实现的因素［3］。能力成熟度集成模型CMMI(capability maturity model in-tegration)是美国卡内基梅隆大学软件工程研究所(SEI)在美国国防部支持下构建的现代企业工程指导性作业体系，融合了6Sigma，TQM，ISO9000等作业体系的核心思路［4］。作为过程域之一，CMMI风险管理体系是CMMI的重要组成部分，其核心思想是提出了“风险管理数据库”的概念。风险管理数据库作为CMMI风险组织级日常管理的输出，在整个CMMI风险管理体系中起到了风险信息汇集、处理、更新的核心工具作用，其模型如图1所示。

图1 风险管理数据库模型

CMMI风险管理的每个子实践(sub practice)与各自特定目标(special goal)内的风险管理数据子库进行单向或者双向的信息传递，以此实现风险管理的各个特定目标，同时风险管理数据子库不断得到输出和更新。在CMMI风险管理过程中，各特定目标内的风险管理数据子库时刻与风险管理数据母库进行库间的信息流动，保证母库得到实时的维护和更新。在整个过程中，各个风险管理环节都要接受项目的计划、监督和控制。

3 委托-代理软件外包博弈视角下，基于CMMI的全过程风险管理结构方程模型

3.1 软件外包全过程风险因素信度与效度检验3.1.1 风险因素数据的收集

通过对文献的梳理，加之笔者在软件外包项目实习中的总结，本文将软件外包全过程风险因素分为3类:发包企业的风险因素、软件外包委托-代理过程中的风险因素，以及接包软件代理公司的风险因素。各类风险包含的风险因子如表1所示。

根据对风险因子的分析概括，设计了企业软件外包全过程风险因素调查问卷。通过实地发放和网上填写，共回收270份问卷，其中有效问卷251份，有效率为92.96%，通过SPSS和Amos统计分析软件对样本数据进行处理。

表1 软件外包全过程风险因子

3.1.2 风险因素数据信度与效度的检验

首先，本文运用SPSS统计软件来分析数据的内部一致性，统计结果显示Cronbach’s Alpha系数是0.895，表明数据具有较好的信度。同时，本文还对每个潜变量的信度进行了检验，3个潜变量的Alpha值均在0.9以上，表明每个潜变量内部之间一致性程度较好。

其次，SPSS验证性因子分析结果显示本文样本数据中含有3个主成份，分别为R1～R7、R8～R14、R15～R203类，符合本文的模型假设，模型整体具有较好的结构效度，理论模型假设成立。

3.2 基于CMMI的软件外包全过程风险管理结构方程模型的构建

结构方程模型是进行社会科学研究的重要工具，可以很好地处理多原因、多结果关系和不能直接测量的变量，有效弥补了传统统计方法的不足［5］。本文将结构方程模型与CMMI风险管理体系相结合，分析和评价各风险因素在软件外包全过程中的关系和影响，以获得更具客观性的综合分析结果。

3.2.1 软件外包全过程风险管理结构方程建模

根据理论模型假设，运用Amos构建企业软件外包全过程风险测量结构方程模型。模型中，F1，F2和F3为潜变量，F1代表发包委托企业方面的风险因素，F2代表软件外包委托-代理过程中的风险因素，F3代表接包软件代理公司方面的风险因素，R1～R20为3个潜变量各自的观测变量。结构方程模型设置完成之后，将研究数据导入Amos中进行配置和处理，准备进行下一阶段的模型拟合工作。

3.2.2 结构方程模型的拟合

结构方程模型的拟合过程本质是采用特定模型算法，对样本协方差矩阵或相关系数矩阵进行模拟，生成最为相近的再生矩阵［6］。Amos提供了多种模型运算的方法，本文采用最大似然估计进行模型拟合。企业软件外包全过程风险测量模型路径图的输出结果如图2所示。

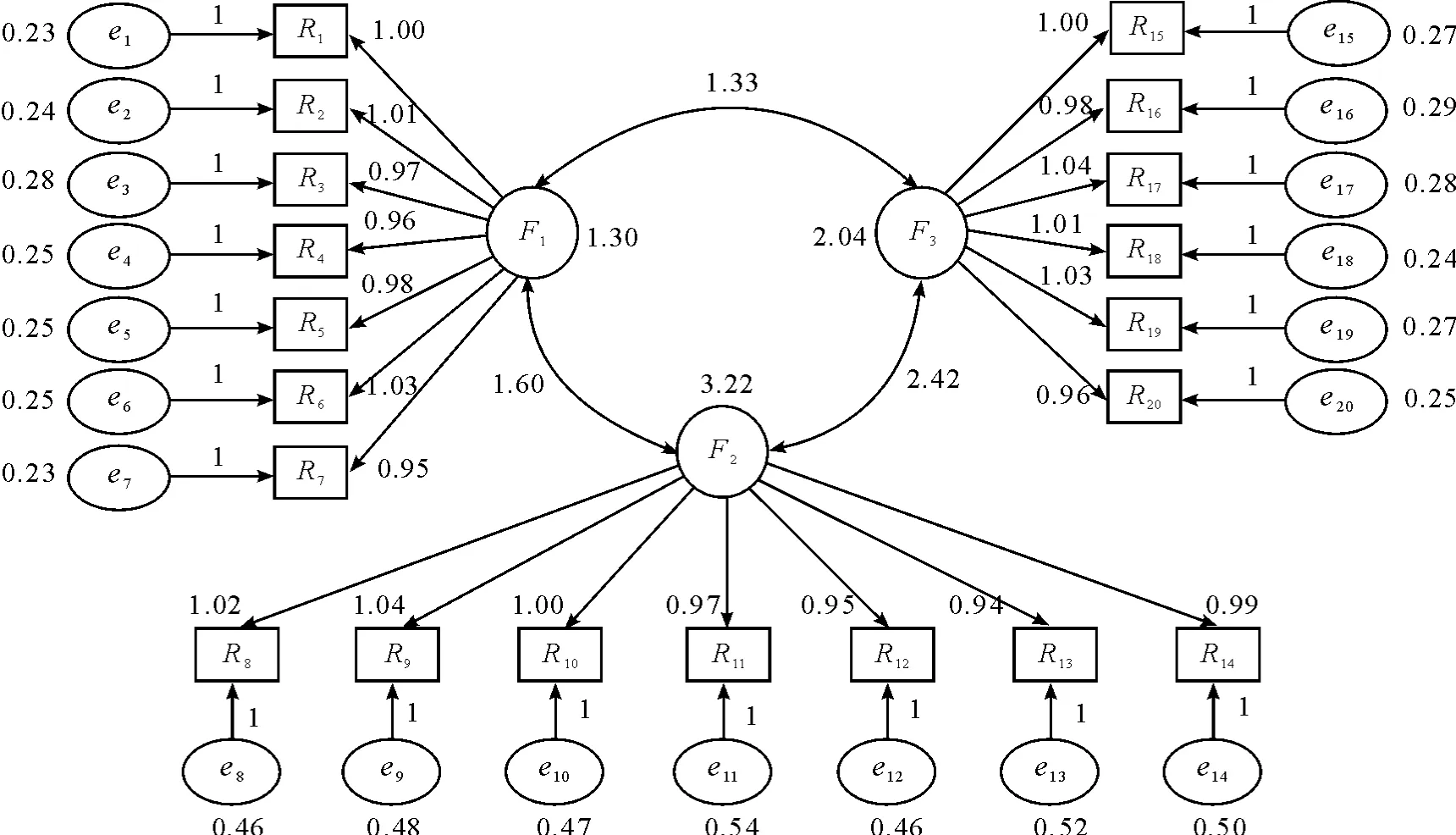
图2 企业软件外包全过程风险测量模型路径图

3.2.3 软件外包全过程风险管理结构方程模型的评价

为了检验模型的效果，本文从以下3个方面对模型进行了拟合优度评价。

首先，进行路径和载荷系数的显著性评价。在进行模型评价时，要分析模型结果中的系数估计结果是否具有统计意义，因此需要对路径和载荷系数进行显著性统计评价。在Amos的负载拟合结果中，p值一列显示所有负载均在0.001水平上显著不等于0，其中 R7←F1，R14←F2，R15←F3是模型固定参数，无需检验。

其次，进行模型中潜变量方差拟合结果的评价。在Amos输出的拟合结果中，Variances表示模型中潜变量的方差拟合结果。拟合结果显示，不存在太大的无意义方差和负值方差，表明本次方差拟合的结果是有效的;同时p值一列的结果表明所有方差均达到了显著水平。

再次，进行模型拟合效果的评价。本文主要通过整体模型拟合度来对模型拟合效果进行评价。整体模型拟合度可以从样本大小、模型复杂度、相对性和绝对性等角度来评价模型与数据的拟合程度与效果。经数据整理，整体模型拟合度指数结果如表2所示。

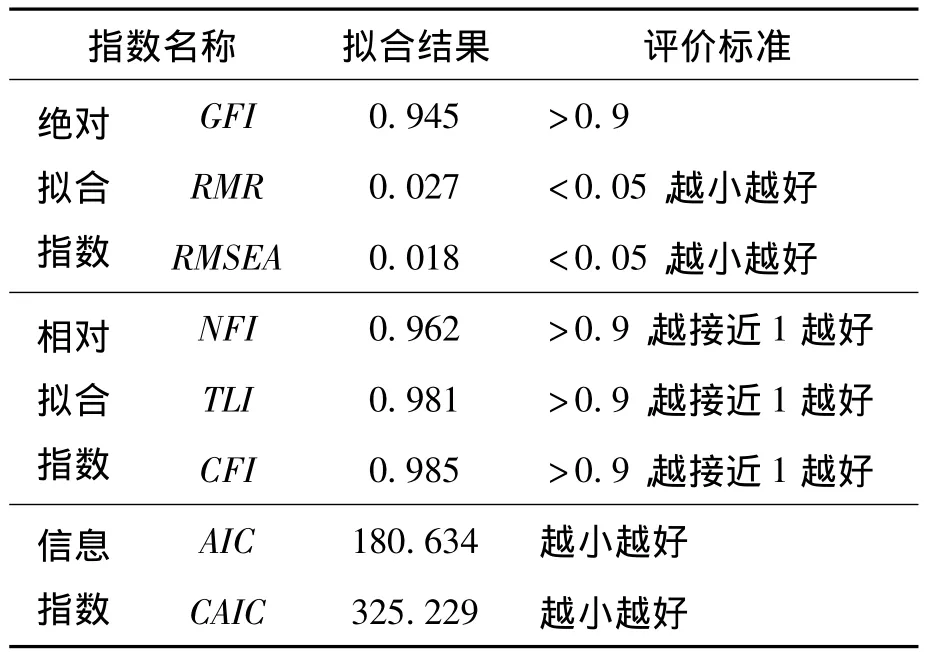
表2 整体模型拟合度指数

从表2的指数结果可知，各指数的拟合结果均符合最优评价标准。其中RMSEA=0.018＜0.05，AGFI=0.931＞0.900，表示模型拟合效果较好。总体来看，该模型达到了可以适配的标准。

3.2.4 结构方程模型拟合结果对软件外包全过程风险管理的启示

基于结构方程模型拟合的结果，本文对企业软件外包全过程风险管理的策略进行了探究和优化，对于企业软件外包风险管理者具有重要的启示意义和实践指导作用。

第一，根据Amos输出结果中潜变量方差的拟合结果，可以得到F1，F2和F3的标准差分别为0.136，0.331和0.206，其中F2的标准差最大，说明F2的波动性最大，最不稳定。因此，为了进行更加科学的风险管理工作，需要将更多的关注点放在稳定性最弱的F2上面，即关注焦点是软件外包委托-代理过程中的风险因素，这一分析结果与CMMI注重过程持续改进的思想相吻合。通过过程的持续改进，合理控制软件外包委托-代理过程中的各项风险因素。

第二，在Amos的输出结果中，潜变量 F1，F2和F3之间的协方差关系如表3所示。

表3 潜变量间协方差和相关性的拟合结果Correlations:(Group number 1-Default model)

注重过程持续改进是CMMI思想的精髓所在。在本文中，F2代表软件外包委托-代理过程中的风险因素，根据图3的拟合结果，F1对F2的权重影响度可以计算为:1.60+1.33×2.42=4.818 6，其中1.60是F1对F2的直接权重影响值，1.33×2.42是F1通过F3对F2的间接权重影响值。同理可以计算出F3对F2的权重影响度:2.42+1.33×1.60=4.548，该值小于 F1对 F2的权重影响值，由此可以看出F1对F2的影响程度更大。在进行软件外包风险过程持续改进工作时，发包企业更需关注自身方面的风险因素，根据风险优先级，对自身风险因素进行有效管控，逐步将CMMI风险管理手段融入到企业自身的风险管理工作中。在此基础上，再对软件外包过程进行持续的优化和改进，降低过程中的外包风险。

第三，从发包企业的角度出发，根据图3协方差的拟合结果，F2对F1的权重影响度为:1.60+2.42×1.33=4.818 6，F3对F1的权重影响度为:1.33+2.42×1.60=5.202，计算结果说明F3对F1的影响程度更大，F3首先直接影响了F1，进而通过过程F2间接影响F1。因此，为了提高软件外包风险管理工作的实践效果，发包企业需要更多地关注F3，即承包软件代理公司方面的风险因素，通过软件外包服务商的遴选机制、软件外包过程中的管理与评估等方式来降低F3方面的风险影响，从而更加有效地降低发包企业承载的风险程度，将风险影响控制在一个可接受、可处理的水平上。

第四，在企业软件外包全过程风险测量模型路径图中，每个观测变量和与之对应的潜变量之间都有相应的载荷系数，该系数可以视为各风险因素在企业软件外包全过程中的风险权重系数。基于CMMI风险管理体系的核心思想，可以将各风险因素按照风险权重系数的大小录入风险管理数据库，根据风险权重系数对风险因素划分相对应的风险等级，使风险管理数据库与实际风险测量数据实现对接，更新和维护风险管理数据库，充分发挥好风险管理数据库功能工具的效用。

3.2.5 模型的修正

尽管通过模型评价可看出企业软件外包全过程风险管理结构方程模型的拟合状况较好，但仍需探究模型进一步完善优化的可能性，因而要进行风险测量模型的修正工作。在Amos的输出结果中带有模型修正的指标，其结果显示未能显著提高模型拟合效果的修正方式。即便是提高效果最好的修正方式，即添加e6和e3之间的协方差关系，也仅能带来0.050个单位的效果优化，而且这种关系的添加并没有充分的理论支持。

4 结束语

风险管理对企业软件外包的管理绩效关系重大。本文将CMMI能力成熟度模型集成理论应用于企业软件外包风险管理中，在“软件外包委托-代理”博弈的最优期望效用条件下，通过构建企业软件外包全过程风险管理结构方程模型，将其与CMMI注重过程持续改进和风险管理数据库的思想衔接融合起来，从发包企业的角度出发，探究进行企业软件外包风险管理工作理念层面的改进和优化。

软件外包服务市场方兴未艾，相关企业卓有成效地做好风险管理工作，将能更好地把握住全球IT服务外包的发展趋势，推动中国软件行业的发展，为促进中国经济的转型升级做出更大贡献。

［1］Peter FDrucker.The New Realities:in Government and Politics，in Economics and Business，in Society and World View［M］.Pennsylvania:HarperBusiness，1994.

［2］Shanshan Li.China-Based Offshore Software Development 2013-2017 Forecast and Analysis［R］.IDC China:Services and Telecommunication Research，2013.

［3］Boyd Donald，Lankford Hamilton，Loeb Susanna，et al.Measuring Test Measurement Error:A General Approach［J］.Journal of Educational and Behavioral Statistics，2013，38(6):629-663.

［4］黄锡伟.CMMI解析与实践［M］.北京:人民邮电出版社，2004.

［5］Mariel F，Ivan A，Jose V，et al.Measurement of An Individual Entrepreneur’s Social Capital:A Multidimensional Model［J］.International Entrepreneurship and Management Journal，2011，7(4):495-507.

［6］Hsu I-Yuang，Su Teh-Sheng，Kao Chen-Shan，et al.Analysis of Business Safety Performance by Structural Equation Models［J］.Safety Science，2012，50(1):1-11.