基于RSSI测距的室内定位研究

周二林，王冠凌

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

随着物联网相关技术的兴起，基于无线传感网络(wireless ensing networks，WSN)和无线局域网(wireless local area networks，WLAN)等面向区域的定位技术越来越受到各行业研究者的关注。面向区域的定位技术是一个前景广阔的研究方向，而室内定位技术是其中的典型代表。在众多定位测距技术中，基于RSSI的测距定位技术通过发射点和接收点之间的信号强度值来估计两点之间的传播损耗，再根据经验模型和相关理论知识将发射节点和接收节点之间的传输损耗转换为两点之间的距离，最后根据相应的算法推算出未知节点的位置。相比其他几种常见的测距定位技术(如到达时间 TOA、到达时间差 TDOA、到达角 AOA等)，接收信号强度指示RSSI的测距定位技术对硬件的要求低、功耗小，且没有时间同步，具有容易实现等优点，得到了广泛的应用。但是复杂的室内环境使得定位精度较低，无法满足正常的室内定位要求。另外，室内环境中人员走动带来的突发性的干扰更使得室内定位的效果很难达到理想的程度，因此寻找一个比较理想的室内环境定位系统已经成为室内定位研究的热点。

1 RSSI定位系统实现框架

在定位理论中，接收信号强度指示值RSSI测距定位技术是通过发射点和接收点之间的信号强度值来估计两点之间的传播损耗，再根据经验模型和相关理论知识将发射节点和接收节点之间的传输损耗转换为两点之间的距离，最后根据相应的算法推算出未知节点的位置。由于室内环境的复杂性，经验模型存在一定的误差，以至接收信号强度值RSSI和未知节点的定位也先后存在不同程度的误差。针对如何更精确的定位，本文提出的基于RSSI测距定位算法的流程如图1所示。

图1 定位系统流程

本文首先利用高斯滤波对采集的RSSI值进行预处理，然后根据数值越大的RSSI值对未知节点位置的参考价值就越大的思想，对高斯预处理后的RSSI值进行加权处理，并对转换后的距离值进行最小二乘法修正。最后，通过判断是否满足判定要求决定是否重新定位。重新定位的次数人为设定，定位通过三边测量算法来实现。

2 RSSI测距定位算法的实现

2.1 盲节点RSSI值的预处理

引用高斯滤波处理数据:首先，在同一个未知信标节点处采集n个RSSI值。由于室内环境的复杂性，往往存在一些小概率事件，通过高斯模型［1-3］滤除一些小概率、大干扰事件，以提高定位的准确性。其次，根据文献［4］室内外环境下RSSI值与距离的衰减关系，当较近距离传输时，RSSI值衰减较快;当较远距离传输时，衰减较慢，接收强度RSSI值相对传输距离的变化表现不明显，即可以观察到RSSI取值在10 m以内的衰减波动较大，在10～15 m衰减比较稳定，距离在15 m以外时，衰减变化很缓慢，因此参考价值比较小。因此，本实验只取前15 m的实验数据以满足更为精确的定位要求。

信标节点可以通过RSSI值计算出未知节点与它的距离，电磁波能量P与路径r的关系模型为其中:a为待定系数;P为能量值;r为距离。

在实际测量过程中，RSSI有一个随机分量x0，即实际测量的数值在一个稳定值附近上下波动，引入高斯模型:

其中:p0服从高斯分布，即 p0～N[ u，σ2]，密度函数为:

其中:xi为第i个信号强度值;n为信号数。

通过在同一个信标节点即同一个位置采集到n个RSSI值，根据采集到的RSSI值与均值u的偏离程度来判别RSSI值的准确性。同时，设定一阈值，当发生小概率的事件或干扰时，若RSSI值偏离均值大于设定的阈值，则排除该RSSI值;若RSSI值偏离均值小于设定的阈值，则保留所测得的RSSI值。

2.2 对信号强度加权处理

本算法的思路:在每个未知节点取n组RSSI值，数值越大的RSSI值对未知节点位置的参考价值越大。在每个测试点取n为100，经过高斯滤波后，对100个数据由大到小排序。取最大的前80个数据，然后将这80个数据分为4组，每组20个数据，分别记为A组、B组、C组、D组。对各组的数据求平均值，分别记各组 RSSIA，RSSIB，RSSIC，RSSID。

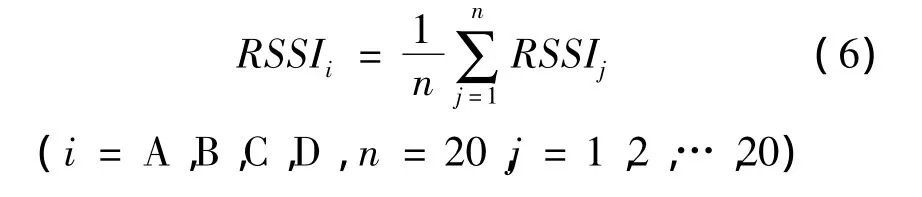
将上面4组数据分别乘以一个权重系数，权重系数值的大小与4组数据平均值的大小有关。假设RSSIA＞RSSIB＞RSSIC＞RSSID，则该参考节点的接收信号强度的平均值为

其中:α，β，χ，δ值的大小分别设为0.5，0.3，0.1，0.1。作为未知信标节点在该位置的信号强度。

2.3 利用最小二乘法修正距离值

在复杂的室内环境中，根据未知节点与信标节点之间的RSSI值估算距离必然存在一定的误差，本文利用传统的最小二乘法对由信号强度转换后的距离值进行修正［5-6］。修正思想是在指定室内区域定位之前，先对特定区域环境进行大量实验定位论证，以获得该环境区域的定位结果的修正公式。方法步骤如下:

①根据具体的实际室内情况布置好参考节点和未知盲节点。假设参考节点坐标为(xi，yi)，盲节点坐标为(xj，yj)，盲节点和参考节点的坐标是人为设定的已知值，可根据两点之间距离公式得到两节点间的实际布置的距离值。

②根据接收信号的信号强度，通过与具体的室内环境相对应的距离损耗模型(式(1))来估算未知节点到各参考信标节点的距离Yi。

③通过最小二乘法来修正实际距离Xi与估测距离Yi的关系。设测距误差值Y与实际距离值X之间存在线性关系，则Y=aX+b。根据最小二乘法原理，偏差平方和最小，则 G(a，b)=最小。通过 G(a，b)分别对a和b求导，令其等于0。则有:

根据真实值和误差值，可求出a和b。那么修正后的距离为

其中:X为修正后的值，Y为距离估计值。通过最小二乘法的修正方法对由RSSI值转换后所对应的距离值进行修正，可得到更加精确的距离值。

2.4 未知节点的坐标估计

针对未知节点的坐标估计采用最典型的三边测量算法，其基本思想是:将这些节点按RSSI值从大到小的顺序排序，选取最大的前3个参考节点作为本次定位的参考节点。通过最大的3个RSSI值得出未知节点到3个信标节点的距离值。已知固定节点(即参考节点)的坐标(x1，y1)，(x2，y2)，(x3，y3)，设未知节点的坐标为(x，y)。通过数学两点之间距离知识可求导出各参考节点与未知节点之间的距离公式，通过两两相减可求出任意两圆的交点所在直线。考虑到两点确定一条直线，3个圆两两相交可确定3条直线，当3条直线有共同交点时，方程组有解，即为未知节点的位置;否则，方程组无解，放弃本次操作，重新获取参数进行定位。通过这3个距离值计算出未知节点的位置［7-8］。

参考节点与未知节点之间的距离公式分别为:

具体步骤:当信标节点 p1，p2，p3收到未知节点p发出的定位信号强度最大时，根据RSSI值，可以得到 p1到 p，p2到 p，p3到 p 的距离 d1，d2，d3;经过修正，分别以 p1，p2，p3为圆心，d'1，d'2，d'3为半径作圆，通过这3个圆可确定未知节点［9］。

1)理想情况下:3圆有共同的交点，相交于P点，则P点坐标就是未知节点的坐标。由于算法操作存在一定的误差，所以实际上3个圆不会相交于一点，而是一小区域面积。

2)实际情况下:由于环境复杂，存在误差，所以一般情况下由3圆组成的区域交点分别为p1(x1，y1)，p2(x2，y2)，p3(x3，y3)。3 个圆两两相交可确定3条直线，判断3条直线是否有共同交点。当有共同交点时，取Δp1p2p3的质心作为未知节点的估计位置。即

3)特殊情况:3个圆两两相交可确定3条直线，这3条直线没有共同交点，即它们没有两两相交，或者3个圆没有任何交点，此时定位误差较大，故放弃本次定位，重新获取RSSI值，重复以上步骤重新定位，最大定位次数通过设定阈值来确定。通过重复定位可以克服一些突发和暂时性的干扰，比如人员的走动等。

3 实验结果分析

实际的实验环境比较空旷，没有固定或移动的障碍物。选择的场地为长18 m，宽6 m的实验室，实验中偶尔有人员走动。最后采用基于 Zigbee协议的CC2430/CC2431芯片为硬件平台，利用RSSI信息来定位待测点的信息。

实验统计数据如表1所示。RSSI均值为经高斯滤波处理后的RSSI值，然后直接求取RSSI均值。RSSI加权值为经高斯滤波处理后的RSSI值，再通过本文的加权算法进行处理后所获得的RSSI值。均值误差为RSSI均值经三边算法定位所产生的误差，加权误差为RSSI加权值再经过最小二乘法修正和三边算法所产生的误差。

首先利用高斯滤波对采集的RSSI值进行预处理，然后根据数值越大的RSSI值对未知节点位置的参考价值就越大的思想，对所获得的RSSI值进行加权处理，再对转换后的测距值进行最小二乘法修正，最后，根据圆之间的交点个数，决定是否重新定位，定位的方法通过三边测量算法来实现。在图2中，实色曲线为本文的处理方法，虚色曲线为以往对RSSI取均值的方法。从图2和表1可看出，本文所采用的测距室内定位算法的误差范围控制较理想，基本可以控制在-0.5～0.7 m，RSSI测距的精度较好。

表1 定位数据表

图2 定位数据对比

4 结束语

本文对高斯预处理后所获得的RSSI值进行加权处理和对转换后的距离值进行最小二乘法修正以提高定位的准确性。通过实验验证了本文方法可提高室内定位精度的有效性和可行性，可基本满足实际生活中的要求。由于本算法不需要增添额外的硬件开销，所以具有较广的实际应用范围和较高的应用价值。

［1］刘文娟.基于RSSI测距的WSN定位系统设计［D］.大连:大连理工大学，2010.

［2］徐世武，王平.ZigBee技术中基于RSSI测距的定位算法研究［J］.福州:福建师范大学，2012.

［3］，Yaghmaee M H，Chiti zadeh J.Three dimension QoS deviation based scheduling in adaptive wireless networks［C］//MProceedings of the 21st International ConferenceAdvanced Networking and Applications.Washington DC:IEEE Computer Society，2007:588-595.

［4］徐久强，刘伟.基于RSSI的WSN抗干扰定位算法［D］.沈阳:东北大学，2010:647-648.

［5］章坚武，张璐.基于 ZigBee的RSSI测距研究［D］.浙江:杭州电子科技大学，2009(2):286-287.

［6］石为人，熊志广，许磊.一种用于室内人员定位的RSSI定位算法［J］.计算机工程与应用，2010，46(17):232-235.

［7］赵昭，陈小惠.无线传感器网络中基于RSSI的改进定位算法［J］.传感技术学报，2009:391-393.

［8］徐日明，庄长远，俞斌.基于 RSSI的动态修正室内无线定位算法［D］.南京:南京航空航天大学，2010:686-688.

［9］臧建魁，卿粼波.基于RSSI和LQI分段距离估计改进算法［J］.通信技术，2011，11(44):100-102.