斜拉索局部振动对结构地震响应的影响*

武芳文，史 俊，杨草方，谢礼立

0 引言

斜拉索是斜拉桥的重要承重结构，在斜拉桥抗震研究中，由于斜拉索的地震反应不控制设计，更为关心整体结构的地震响应。拉索作为柔性结构单元受到两端支点的扰动作用时容易诱发索的局部振动，拉索的局部振动不但改变斜拉桥振动能量的分布、影响振动体系的阻尼特性，同时还可能因拉索与结构整体间的内部共振引起复杂的结构动力特性。在采用有限元分析时，通常采用单根桁架单元来模拟斜拉索，但不能反映斜拉索局部振动对桥梁地震反应的影响。斜拉索的局部振动不仅会影响斜拉桥的动力特性，还会影响索梁耦合共振等复杂的非线性动力学现象。随着斜拉桥跨度的增大，斜拉索的长度必然增大。因此，研究大跨度斜拉桥拉索局部振动对结构地震响应的影响是很有必要的。

斜拉索局部振动对整体结构地震响应影响研究中，叶爱君和苏振宇 (2010)以苏通长江公路大桥为背景，采用多桁架模型考虑斜拉索局部振型，将斜拉索分为10个单元考虑拉索局部振动效应研究其对对结构地震响应的影响;布占宇等(2006)通过分析杭州湾大桥的地震反应，认为考虑斜拉索的局部振动后，斜拉桥纵向振型的参与系数有不同程度的减小，主梁和桥塔的加速度、位移、弯矩和轴力增大非常显著，短索的纵向位移减小，而长索的纵向位移增大。Abdel Ghaffar(1991)研究了斜拉索局部振动对斜拉桥动力特性的影响，得出斜拉索的局部振动对某些振型的参与系数有影响，在计算地震反应时应该考虑索的局部振动的结论。Ali和Abdel Ghaffar(1995)研究了索的局部振动对斜拉桥动力特性的影响，认为索的局部振动对某些振型的振型参与系数有较大影响，在斜拉桥地震响应计算中应考虑拉索的局部振动。

本文以苏通长江公路大桥为背景，全桥斜拉索长度为153～578 m，将斜拉索按照100 m标准分成若干等长度单元。采用有限元程序ANSYS，以随机振动理论为基础，将地震动作为随机模型，建立地面加速度功率谱密度模型，分析斜拉索局部振动对结构地震响应的影响。

1 随机地震动场的模拟

空间地震动场的模型应尽可能体现地震动特征，一般来说，已知地震动场的各点自功率谱，各点互功率谱可以表示为 (杜修力，陈厚群，1994;王光远等，1999)

式中，Sjj(ω)、Skk(ω)为 j、k两点自功率谱，ρjk(d，ω)为j、k两点地震动的相干函数，描述两点地震动相关程度，d为两点在地震动传播方向上的距离。本文采用的相干函数模型为屈铁军—王君杰—王前信相关函数模型 (屈铁军等，1996):

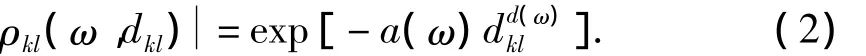
其中，a(ω)=a1ω2+a2，b(ω)=b1ω +b2。a1=0.000 016 78，a2=0.001 219，b1= －0.005 5，b2=0.767 4。该模型综合了以SMART－1为主的4个密集台震的几十次地震记录，应用效果较好。

地震波视波速Va(ω)是研究地震动空间变化的一个参数，其表达式为

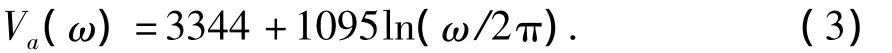
自1957年日本学者Kanai-Tajimi提出过滤白噪声随机地震动平稳功率谱模型之后，许多学者提出过改进模型，本文采用杜修力—陈厚群模型(杜修力，1998)，其表达式为

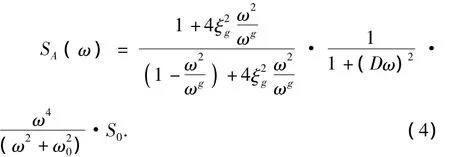
2 基于ANSYS/PSD的随机地震反应分析方法

随机振动分析方法充分考了地震动在时间和空间上发生的统计特性，采用相关函数描述各点动力响应的相关性，被认为是一种较先进合理的分析方法

对于多自由度线性振动体系的地震反应分析，假定动力方程中的阻尼项为经典阻尼，结构的动力相对位移可以用振型广义坐标表示为{ufd(t)}=［φ］{y(t)}，并代入方程可得:

足球专项教师要加强自身的足球理论知识的学习，不断学习国内外先进的足球教学理念和经验，还要提高足球技术技能。同时，在上足球课中能做到示范准确，展现良好的技能，为学生树立好的足球学习榜样。

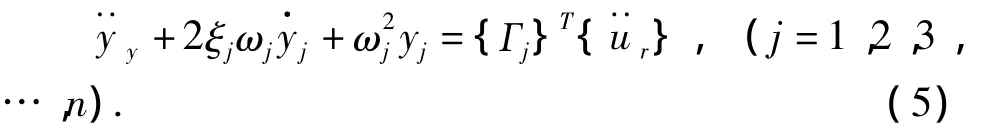
式中，n为需要计算得振型数;yj为第j振型的广义位移;ωj、ξj为第j振型的自振圆频率和模态阻尼比;{Гj}为相应于基础激励的振型参与系数，可表达为

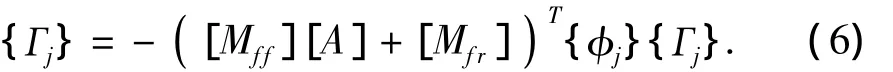
在非一致激励随机振动分析中，随机荷载是以功率谱密度函数的形式来施加的，其输入的PSD可采用下列通用形式

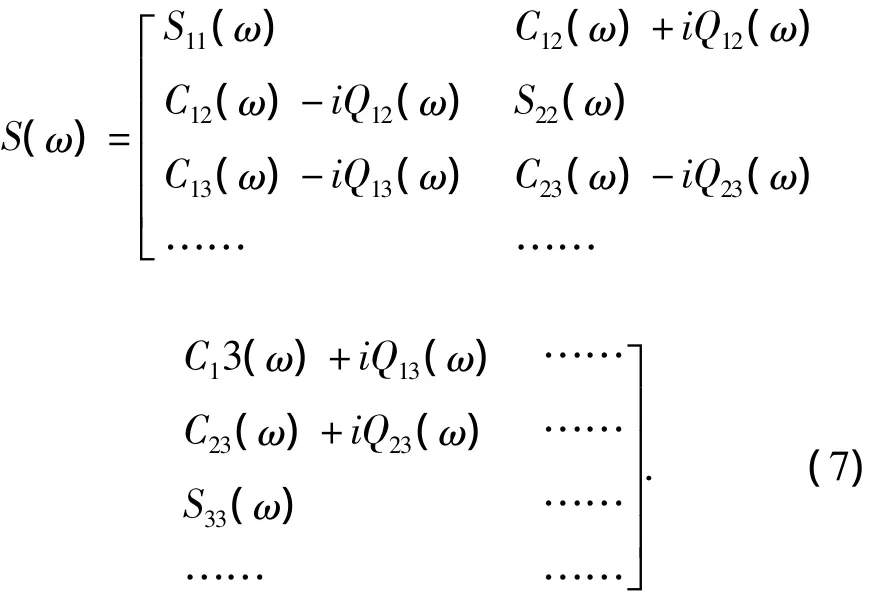
式中，Sii(ω)为自功率谱;Cii(ω)为互谱实部;Qii(ω)为互谱的虚部;其2≤n≤10。

在多点激励的功率谱分析中，各激励点可以按如下的PSD关系式输入

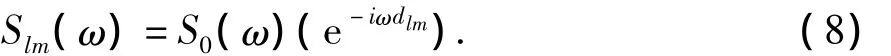
3 动力分析模型

3.1 工程背景

苏通长江公路大桥位于长江下游，双塔双索面斜拉桥，主桥跨径为 (100+100+300+1088+300+100+100)m。主桥钢箱梁共分为17种类型、141个梁段，节段标准长度16 m、边跨尾索区节段标准长度12 m。塔柱采用倒Y形结构，分为下塔肢、中塔肢、上塔肢和横梁四部份。中、下塔肢为钢筋混凝土结构，上塔肢为钢锚箱—混凝土组合结构，索塔高300.4 m。斜拉索为Φ7平行钢丝体系，全桥共34×8=272根斜拉索，如图1所示。

3.2 有限元模型

采用大型通用有限元分析软件ANSYS进行结构分析。在建立空间模型时，主要作了下列处理(武芳文，2008;武芳文，赵雷，2009):(1)用“鱼刺梁”模拟主梁，主梁采用beam44模拟;(2)主塔采用beam44模拟;(3)斜拉索采用link8模拟;(4)斜拉索与主梁之间的连接采用“鱼刺”与主梁连接，“鱼刺”用刚度很大 (相对于主梁刚度)的beam4梁单元模拟;(5)辅助墩及过渡墩采用beam44模拟;全桥共离散为1 541个节点，2 393个单元，其有限元模型如图2所示。

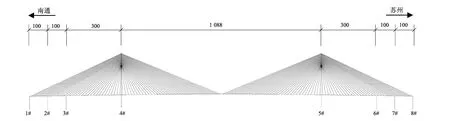
图1 苏通长江公路大桥主桥结构布置图Fig.1 Layout of Sutong Yangtze River Highway Bridge

图2 苏通长江公路大桥有限元模型Fig.2 FEA model of Sutong Yangtze River Highway Bridge

4 斜拉索基频与地震响应分析

4.1 斜拉索基频计算

静力分析用一个杆单元模拟斜拉索对结果有足够的精度，但动力地震响应分析时，其不能考虑斜拉索的横向振动对结构响应的影响。使用等效弹性模量方法时，一个杆单元模拟一根索，将忽视斜拉索的横向振动模态。因此，不能考虑斜拉索和结构之间的动力相互作用。本文的计算模型将斜拉索分为若干个杆单元来模拟斜拉索，研究斜拉索振动效应对结构动力响应的影响 (周宝峰等，2013)。

假定斜拉索其中的一段长度为Δx，两端固定，如图3所示。斜拉索的张力为T，μ为斜拉索的单位长度质量，在时间t时刻，根据平衡条件可得:

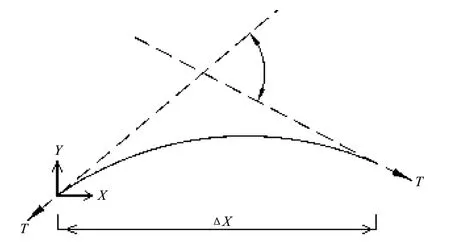
图3 斜拉索振动示意图Fig.3 Schematic diagram of stay cable vibration

然后利用边界条件可得斜拉索的第n阶频率为

于是斜拉索的第一阶频率为

当斜拉索的支撑点移动时，斜拉桥中斜拉索的实际状态和上述条件有所差别，但式 (11)仍可用来计算斜拉索的自振频率，其精度还是可以接受的。

计算斜拉索自振频率的公式可以由斜拉索的应力来表示。令σ、ρ和A分别为斜拉索的应力、密度和面积;于是斜拉索的索力T=σA，单位长度索的质量为μ=ρA，因此式 (11)可以表示为:

由式 (12)计算苏通大桥的斜拉索的第一阶频率如表1所示。全桥斜拉索的第一阶频率在0.214 5～0.827 4 Hz之间 (图4)。而苏通桥前30阶频率在0.075 8～0.923 7 Hz范围之内。可见，斜拉索的基频与斜拉桥自振频率的前几十阶非常接近，于是斜拉索的振动对斜拉桥结构的振动的影响不能忽视。

4.2 考虑斜拉索局部振动的地震响应分析

通过计算分析，考虑斜拉索振动的影响，需要把一根斜拉索分为多个单元，斜拉桥的自振特性发生了变化，因此，结构的动力响应也会随之变化。通过两种模型分析斜拉索振动对斜拉桥结构响应的影响，其计算结果如图5～7所示。考虑斜拉索振动效应时，需要把斜拉索分为多个单元模拟。若把每根索分为很多单元来模拟，会增大计算困难，本文中模型1以索长100 m为单位进行划分，如A1(岸侧1号索)索长153.434 m，就把它等分为两个杆单元;而J34(江侧34号索)索长578.589 m，就把它等分为六个杆单元。模型2的斜拉索为一个杆单元模拟。其结构自振频率如表2所示，用多单元模拟斜拉索考虑斜拉索振动效应时，结构的自振频率有所降低。

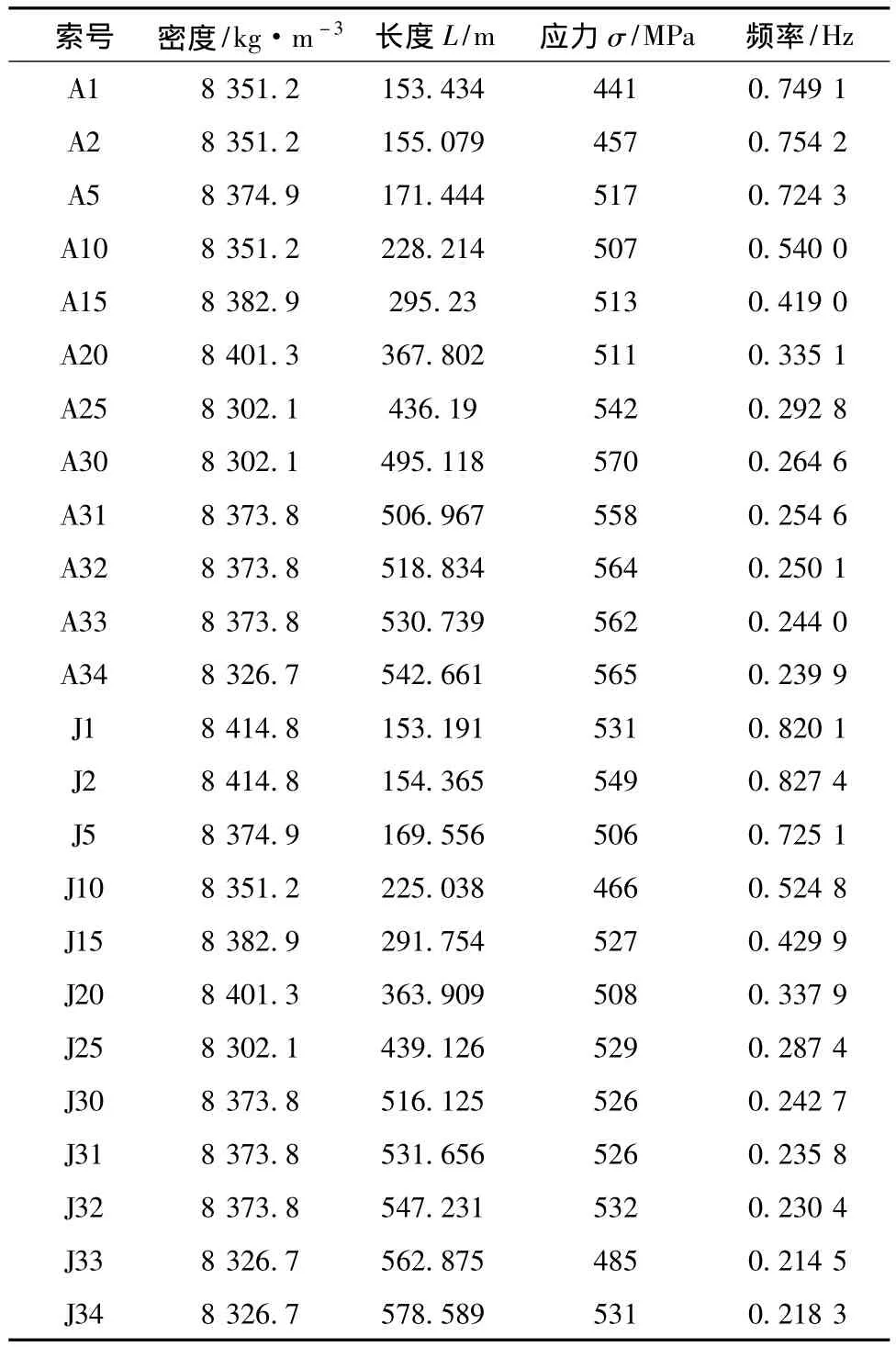
表1 苏通大桥斜拉索的第一阶频率Tab.1 The first order frequency of stay cable of Sutong Bridge

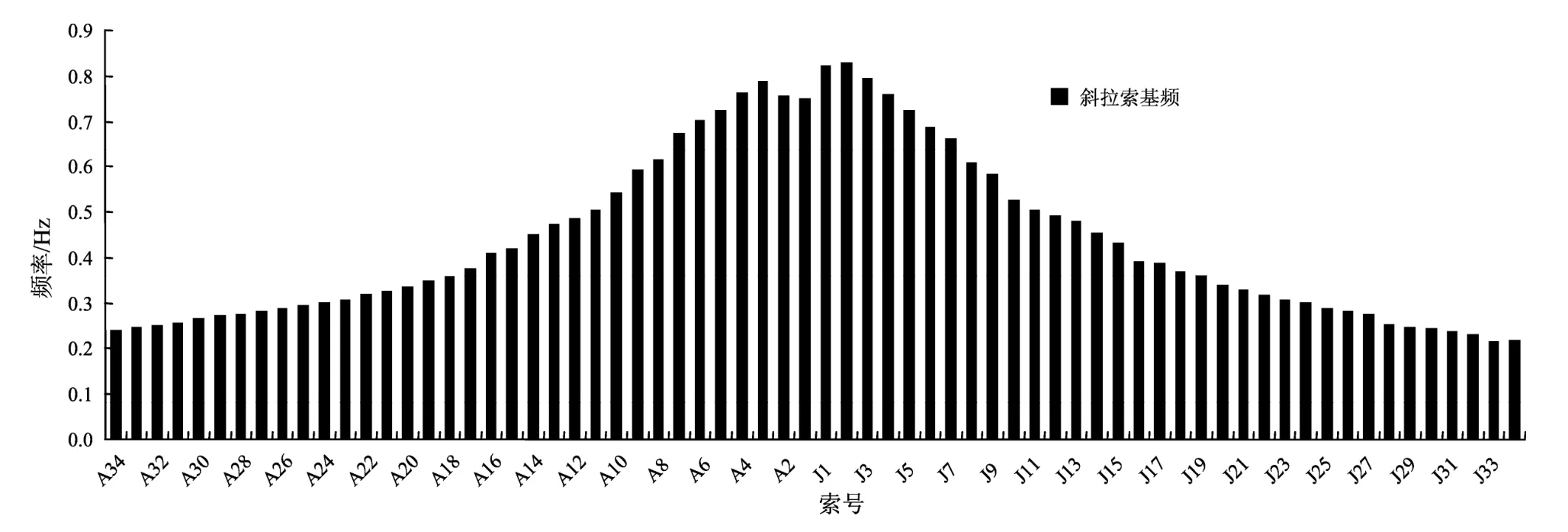
图4 苏通桥斜拉索基频图Fig.4 The fundamental frequency of stay cable of Sutong Bridge

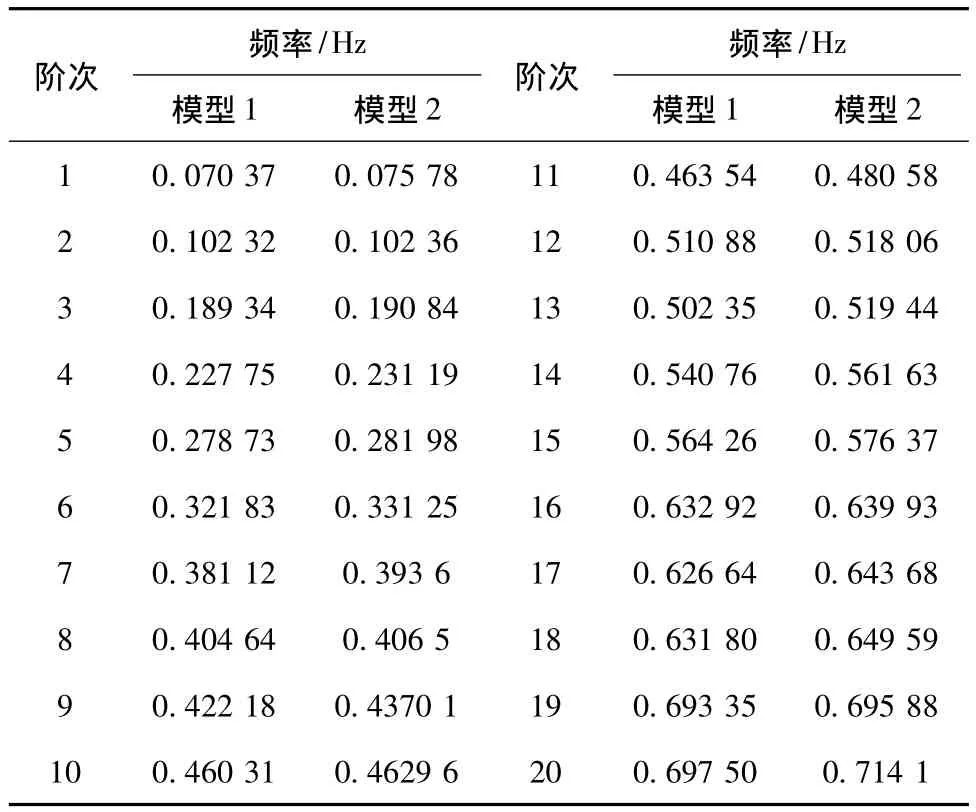
表2 结构自振频率Tab.2 Natural vibration frequency of the structure

以上述理论模型为基础，分析斜拉索局部振动结构地震响应的影响。从图5～7计算分析结果可见，斜拉索振动对主梁的某些部位响应有所减小，尤其在辅助墩处变化更为突出。考虑斜拉索振动效应后，主梁纵向弯矩MZ减小了53%;竖向位移均方根减小了45%;主塔塔根纵向弯矩MZ减小了13%。可见，斜拉索振动效应对结构内力的影响不能忽略，考虑斜拉索振动效应后结构内力均有减小趋势，可见对结构有利。

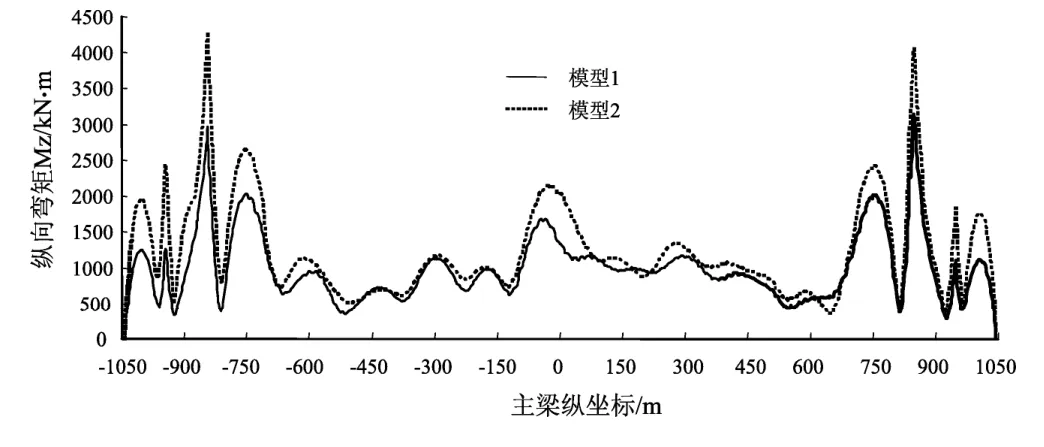
图5 主梁纵向弯矩MZ均方根Fig.5 RMS of longitudinal bending moment MZof girder

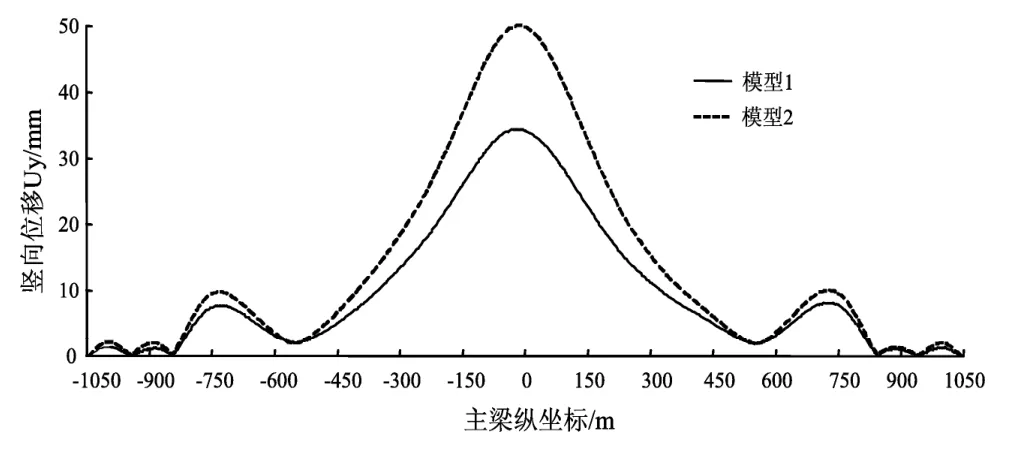
图6 主梁竖向位移Uy均方根Fig.6 RMS of vertical displacement Uyof girder

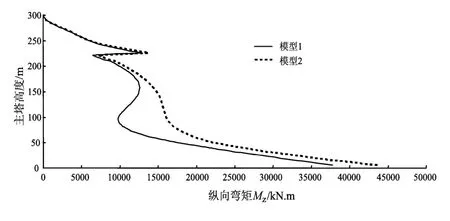
图7 北塔纵向弯矩MZ均方根Fig.7 RMS of longitudinal bending moment MZof the North Tower

斜拉索与结构振动之间的相互作用不仅影响了结构的振型，同时对主塔和主梁结构动力响应有明显的影响。因此，在分析长周期大跨度斜拉桥结构时，不应该忽视斜拉索振动效应，尤其斜拉索的第一阶频率与整体结构自振频率前几十阶频率重叠时。

5 结论

本文以苏通长江公路大桥为研究对象，采用随机振动分析方法，将斜拉索单元分成若干等长度单元模拟斜拉索局部振动效应。通过考虑索的局部振动的斜拉桥动力特性和地震响应分析，得到以下结论:

(1)斜拉索的长度越大，其基频越小，全桥拉索基频在0.749 1～0.218 3 Hz，长索的在地震动作用下，大幅振动，索—梁耦合振动明显。

(2)采用此方法考虑斜拉索局部振动效应，对结构的自振频率影响较小。

(3)斜拉索基频与结构基频相近时，主梁和主塔内力降低，主塔根部弯矩明显减小。

布占宇，谢旭，苟昌焕.2006.拉索局部振动对斜拉桥地震反应的影响研究［J］．工程力学，23(9):157 －166.

杜修力，陈厚群.1994.地震动随机模拟及其参数确定方法［J］．地震工程与工程振动，14(4):1－5.

杜修力.1998.水工建筑物抗震可靠度设计和分析用的随机地震输入模型［J］．地震工程与工程振动，18(4):76－81.

屈铁军，王君杰，王前信.1996.空间变化的地震动功率谱的实用模型［J］．地震学报，18(1):55 －62.

王光远，程耿东，邵卓民，等.1999.抗震结构的最优设防烈度与可靠度［M］．北京:科学出版社，100－123.

武芳文，赵雷.2009.地震动空间变异性对千米级斜拉桥结构随机地震反应的影响［J］．地震工程与工程振动，30(5):89－94.

武芳文.2008.大跨度斜拉桥随机地震响应分析及其动力可靠度研究［D］．成都:西南交通大学.

叶爱君，苏振宇.2010.超大跨径斜拉桥斜拉索局部振动对地震反应的影响［J］．同济大学学报(自然科学版)，38(2):158－163.

周宝峰，温瑞智，于海英，等.2013.一种识别永久位移的新方法［J］．土木工程学报，46(增刊2):135－140.

Abdel Ghaffar A.M..1991.Importance of cable vibration in dynamics of cable － stayed bridges［J］．Journal of Engineering Mechanics，117(11):2571－2563.

Ali H.M.，Abdel-Ghaffar A.M..1995.Modeling the nonlinear seismic behavior of cable － stayed bridges with passive control bearings［J］．Computers＆ Structures，54(3):461－492.