页岩气藏体积压裂产能影响因素分析

董 浩，马 轮，韦乐乐，王丽娜，王 芳，宋德彬，赵思琦，王 云

(1.西北大学大陆动力学国家重点实验室/西北大学地质学系，陕西西安 710069;2.中国石油勘探开发研究院西北分院/中国石油天然气集团公司油藏描述重点实验室，甘肃兰州 730020;3.中国石油天然气管道局第四工程分公司，河北廊坊 065000;4.中国石油集团长城钻探工程有限公司测井公司辽河项目部，辽宁盘锦 124010;5.中石油管道公司西安输油气分公司，陕西西安 7100185)

由于页岩气储层渗流条件非常差，目前对于页岩气藏的开发还局限于单井。页岩气藏单井开发效果的影响因素［1～8］很多，既有基质渗透率、天然裂缝发育程度等决定页岩气藏开发效果的客观因素，又有压裂改造程度、生产制度等决定页岩气藏开发效果的主观因素。另外，页岩气解吸作用和扩散作用等也会对产能产生不可忽略的影响［9～15］。本文通过对以上诸多因素进行全面分析，为页岩气藏体积压裂的产能影响因素进行权重分析，进而为开发不同条件的页岩气藏提供理论指导。为了方便对比，本文采用一套模型参数(表1)。

表1 模型基础参数表Table 1 basic parameters of model

1 基质渗透率

页岩气藏基质是气体的主要储存空间，气体首先通过基质运移到天然或人工裂缝中，然后由裂缝流入井筒，因此页岩气藏基质的渗透率大小对产能的影响很大［16］。考虑到模型计算能力不能过大，假设水平段长为600m，压裂人工裂缝6段，每段分为3簇，簇间距为25m，人工裂缝渗透率为200mD，缝长为150m，天然裂缝与人工裂缝正交分布，长度由内向外逐渐减小，缝间距为25m，通过局部网格加密实现，水力压裂后裂缝示意图如图1所示。

图1 人工裂缝和天然裂缝分布示意图Fig.1 Distribution of Artificial fractures and natural fractures

通过调整页岩基质渗透率来模拟其对单井产量的影响，基质渗透率Km由0.0001mD增加到0.01mD，模拟得到日产气量和10年累计产气量(图2)。从图2可以看出，基质渗透率越大，初始日产量越高，日产气量下降越快。当基质渗透率Km小于0.001mD时，基质渗透率的增加对日产气量的影响不大，基质渗透率Km从0.0001mD增加到0.0005mD时日产气量增加不大，生产1000天后两者的日产气量基本没有差别;而当基质渗透率Km大干0.001mD时，基质渗透率的增加对日产气量的增加影响较大。由图2可见，当基质渗透率Km从0.001mD增加到0.005mD时，日产气量增加幅度较大，特别是初期日产气量的增幅更大。出现这种现象的原因是，当基质渗透率过小时 (小于0.001mD)，气体在基质中的流动很困难，基质渗透率即使成倍的增加对气体的流动改善也非常有限;而当基质渗透率相对较大时 (大于0.001mD)，稍微增加基质渗透率就能较大幅度地提高日产气量。可见，当基质渗透率大干0.001mD时，渗透率的增加对于页岩气产能的影响要大。

图2 不同基质渗透率条件下产气量对比图Fig.2 Comparison of gas production rate for different matrix permebilities

图3所示为不同基质渗透率页岩气藏10年末储层压力图，从图中可以看出，当基质渗透率Km为0.0001mD时，10年末的压力降还围绕在人工裂缝和天然裂缝之间，说明渗透率太小气体流动困难，压力外扩的速度比较慢。随着基质渗透率的增加，10年末的压力降范围逐渐扩大。低渗透率时人工裂缝间的气体难以波及到，气体无法动用，然而当基质渗透率为0.005mD时，人工裂缝间的压力降逐渐连成一片，说明人工裂缝间的区域也得到了动用，期间的页岩气随着压力的下降而流入裂缝，进入井筒被采出。当基质渗透率Km为0.01mD时，裂缝间的压力降与裂缝内的压力降基本一致，说明裂缝间的页岩气得到了很好的动用，这也是不同基质渗透率对产能影响的根本原因。

图3 不同基质渗透率条件下的10年末储层压力图Fig.3 Formation pressure distribution after ten－year production for different matrix permeabilities

2 人工裂缝参数

目前页岩气藏的开发主要通过大规模水力压裂方法，因此人工裂缝对于页岩气藏产能的影响很大。人工裂缝参数主要包括裂缝长度Lf(即裂缝半长)、裂缝导流能力Df及裂缝条数Nf。模拟过程中，假设水平段长1000m，天然裂缝仍然平行于水平井筒分布，具体参数如表1所示。

2.1 裂缝长度

通过调整裂缝半长Lf来模拟裂缝长度 (简称缝长)对页岩气藏单井日产气量和累计产气量的影响 (图4)。图4a所示为裂缝半长Lf从75m增加到200m时日产气量的变化，从图中可以看出，随着裂缝半长的增加，日产气量增加;且裂缝半长越大，初期日产气量越大 (当裂缝半长Lf为75m时，初期日产气量为23×104m3，当裂缝半长Lf为200m时，初期日产气量为37×104m3。同时，随着裂缝半长的增加，日产气量的递减率增大，到10年末时，裂缝半长为200m的日产气量只比裂缝半长为75m的日产气量多1000m3左右。从图4b中可以看出，随着裂缝半长的增加，10年累计产气量增加，且产量的增加与裂缝半长的增加基本对应，即裂缝半长每增加25m，累计产气量的增幅基本相同。

图5所示为不同裂缝半长下10年末的压力分布图，图中仅显示了裂缝周围相同区域内的压力分布。从图5中可以看出，裂缝半长越小，10年末的压力波及区域越小，这充分说明丁人工裂缝长度对产量的影响程度。众所周知，低渗透油气藏中，人工裂缝的作用相当于交通运输中的高速公路，由于油气藏的低渗透性，应尽可能地修长高速公路，使更多的油气流入其中，这样才更有利于疏导交通。若裂缝半长较小，裂缝控制范围就小，其外的油气藏很难流进裂缝这条高速公路里，也就很难被采出。显然，对于页岩气藏的超低渗透率的储层来说，裂缝半长的意义更加重要。

图4 不同裂缝半长条件下的产气量对比图Fig.4 Comparison of gas production rate for different fracture lengths

2.2 裂缝导流能力和裂缝条数

裂缝导流能力为裂缝渗透率与裂缝宽度的乘积。裂缝导流能力的大小表征了裂缝运输油气的能力，裂缝导流能力越大，输气能力越强;反之，输气能力越弱［17］。通过调整人工裂缝的裂缝导流能力来模拟其对页岩气藏单井产能的影响，当裂缝导流能力从10D·cm增加到40D·cm时，累计产气量几乎没有增加，这与低渗透油气藏中裂缝导流能力越大产量越高不吻合，这一现象主要是由页岩气藏的渗透率极低造成的。当裂缝导流能力为10D·cm时，人工裂缝的输气能力已远超过页岩基质的输气能力，裂缝导流能力再增大到40D·cm时产量也不会有明显增加。这一现象也可用高速公路来比喻，当车流量很小时，双车道和4车道的高速公路的运输能力可能是相当的，增加车道数不会对运输能力有大的提高。

图5 不同裂缝半长条件下的10年末储层压力分布图Fig.5 Formation pressure distribution for different fracture lengths

由于页岩气藏储层的致密性和人工裂缝的局限性，天然裂缝的复杂程度对页岩气单井产能具有决定性的意义。若天然裂缝非常发育，则很少的人工裂缝就能产生很好的沟通作用，形成很大的改造体积;若天然裂缝极其不发育，则在目前的工艺条件下，再多的人工裂缝也无法对储层产生较好的改造作用。基于对人工裂缝参数的优化，选取人工裂缝条数为6条、裂缝导流能力为10D·cm、裂缝半长为200m，通过调整天然裂缝参数分析其对页岩气单井产能的影响。将裂缝条数从2条增加到12条来模拟其对页岩气单井产能的影响。为了模拟不同的裂缝条数，需要对模拟区域进行不同形式的网格加密，工作量很大，为了计算简便且不影响结果，以加密12条缝的情况对模拟区域进行加密，而后根据不同的需要对表示裂缝的网格进行不同的设置来模拟人工裂缝，当裂缝条数达到10条或12条时，10年末的压力已经覆盖了整个加密区域，对加密区域外仅有少部分波及，在这种情况下可以将加密区域视为一个小气藏，外部的气体很难流入裂缝中被采出来。值得注意的是，当裂缝条数从2条增加到6条时的累计产气量增加非常巨大，而当裂缝条数大于6条之后，累计产气量随裂缝条数的增加的幅度不明显。这是因为当裂缝条数大于6条后，多余的裂缝条数对于改造体积的增加意义不大，因此10年末的累计产气量增加不大。由此可知，对于本例，6条裂缝的效果最佳。

3 天然裂缝参数

3.1 裂缝导流能力

按照之前的高速公路理论，天然裂缝导流能力相当于链接高速公路的辅路的运输能力，导流能力大则允许进入人工裂缝的油气流大，在油气量足够大的情况下，裂缝导流能力越大，高速公路的运输能力就越强。因此，调整天然裂缝导流能力从0.1D·cm至5.0D·cm，分析裂缝导流能力的增加对累计产气量的影响。随着天然裂缝导流能力的增加，10年累计产气量逐渐增加。相比于天然裂缝导流能力从1.0D·cm增加到5.0D·cm时的累计产气量增幅，天然裂缝导流能力从0.1D·cm增加到0.5D·cm时，累计产气量的增幅更大，这主要是因为裂缝导流能力从0.1D·cm到0.5D·cm之间的天然裂缝的渗流性已经比基质系统有很大的提升，多余的裂缝导流能力增量也起不到大幅增加产气量的作用［18，19］。

3.2 天然裂缝间距

天然裂缝间距，即两条天然裂缝间的距离。假设天然裂缝与水平井筒平行，与人工裂缝垂直，因此天然裂缝的不同间距表示人工裂缝与储层的连通性。天然裂缝间距小，说明其密度大，与人工裂缝的连通性好;天然裂缝间距大，说明其密度小，与人工裂缝的连通性差。由于前文假设人工裂缝半长为200m，所以对于间距大于200m的天然裂缝的模拟是没有意义的。基于此，天然裂缝导流能力设为0.5D·cm，假设天然裂缝的间距分别为25m、50m、75m及100m，模拟不同间距条件下页岩气藏单井产能情况。为了考虑极端情况，增加间距为零的情形表征不存在天然裂缝的情况。

由表2可知:当无天然裂缝时，单井初期日产气量较低，存在天然裂缝的井初期日产气量较高。随着天然裂缝间距减小，初期日产量快速增加。天然裂缝间距由25m增加到50m时，初期日产气量大幅度下降，而从50m增加到100m过程中，初期日产气量下降的幅度减缓。这说明当天然裂缝间距为25m时，能够相对较好地对裂缝泄气区域进行覆盖，而一旦天然裂缝密度降低，达不到覆盖裂缝泄气区域所需要的密度时，初期日产气量就会大幅下降。因此，对于页岩气藏的开发，天然裂缝的发育程度越强越有利。

表2 不同天然裂缝间距时的初期日产气量表Table 2 initial daily rate for different fracture interval

3.3 天然裂缝分布

实际地层中天然裂缝分布非常复杂，很难通过数值模拟方法准确表征，更无法进行因素分析。为了对天然裂缝的分布状况进行模拟，考虑了以下3种情况，即不存在天然裂缝的情况、天然裂缝不完全连通的情况及天然裂缝完全连通的情况。不存在天然裂缝的情况可以理解为天然裂缝完全不连通，页岩气的开发依靠基质和人工裂缝渗流;天然裂缝不完全连通，是指存在相互不沟通的天然裂缝;天然裂缝完全连通，是指天然裂缝完全贯通整个人工裂缝系统，人工裂缝与天然裂缝形成裂缝网络［20～23］。

对于天然裂缝完全连通的情形，改造区域内的页岩气初期动用比较充分;而对于天然裂缝不完全连通或无天然裂缝的情形，改造区域内的页岩气在初期无法被充分动用，因此初期日产气量比较小。但是，随着改造区域内气体的采出，完全连通情况下的日产气量的下降速度比另外两种情况快得多。

4 敏感因素分析及改造体积

由前述分析可以看出，不同参数对产能的影响最终都归结为改造体积的大小对产能的影响，这一点与低渗透油藏非常相类似。在低渗透油藏的开发中，单井泄油面积对产能有直接影响，而泄油面积的大小又与地层渗透率、人工裂缝参数等因素有关［24，25］。因此，对页岩气藏产能的影响因素进行深入研究非常必要，即找到影响改造体积的几个关键因素，这对页岩气藏初期开发方案制订有着非常重要的意义。本文首先采用正交试验方法对以上各因素进行综合评价，找出3个对产能影响最大的因素;然后根据其影响程度的大小设计方法绘制图版;最后通过一种BP人工神经网络的方法确定任意条件下的改造体积，为页岩气藏快速产能预测提供有效方法。

4.1 正交试验方法

单因素或双因素试验，实施起来较为简单。但是当考察的因素在3个或3个以上时，进行全方位的试验规模将异常庞大。通常情况下，当试验因素过多时，试验方案太多而导致试验不可行。正交方法设计可以解决这一难题，它是一种高效的针对多因素、多水平的优化方法。它通过从总体实验方法中挑选出具有代表性的试验，对它们进行评估来找出最优的组合，即可以从一部分试验了解到全部试验。当试验因素比较多时，正交法可以大幅度降低试验的次数，从而使开展试验成为可能。

正交试验包括两个要素:因素和水平。因素是指试验的项目，如前述的基质渗透率、人工裂缝长度等;水平是指每个因素的取值个数，如基质渗透率从0.0001mD增加到0.0005mD为5个水平。正交试验具有水平均匀性和搭配均匀性的特点。水平均匀性是指所选的方法对每个因素及其对应的水平都是均匀分配的;搭配均匀性是指每个因素的每个水平在所有方案中出现的次数相同，且任意两个因素的搭配以相同的次数出现。

由于需要对比的因素依然非常多，首先需要对各单因素分析定性筛选出比较敏感的因素重点研究。如前所述，人工裂缝长度对产能的影响比较大，为非常敏感的参数;裂缝数量在大于6条后，其对产能的影响非常小，可以忽略不计;而裂缝导流能力相对于基质渗透率非常大，因此它的敏感性很弱。对于天然裂缝参数，当天然裂缝的导流能力大于0.5D·cm后，产能对导流能力不敏感;天然裂缝的间距对产能的影响很大;由于页岩气的开发效果受天然裂缝的连通性影响太大，为了避免天然裂缝的分布对结果的影响太大造成偏差，这里不把天然裂缝分布作为正交试验的因素。另外，页岩气开发中气体解吸对后期产能的影响不容忽略，基质渗透率同样对产能影响很大，因此认为基质渗透率、人工裂缝长度、天然裂缝间距及气体吸附比为正交试验的4个合理因素。

若要得到各因素对指标影响的主次关系，需要对正交试验各个方案的结果进行极差分析。极差反应了各因素的水平变化时，指标的变化幅度，即当基质渗透率、人工裂缝长度、天然裂缝间距及气体吸附比例变化时，页岩气藏单井10年累计产气量的变化幅度。

4.2 影响因素的排序

为了模拟基质渗透率、人工裂缝长度、天然裂缝间距和气体吸附比等4个因素对产能影响的主次关系，假设水平段长1000m，人工压裂6段，每段3簇，人工裂缝导流能力为10D·cm，天然裂缝导流能力为0.5D·cm，天然裂缝不完全连通，每个因素分别取5个水平 (表3)。

表3 正交试验中各因素的水平值表Table 3 Factor values in orthogonal test

通过正交设计，得到了25种方案，对模拟结果进行极差分析。首先将各因素、各水平对应的指标数值相加，如对应基质渗透率的Kl，值即为0.0001mD的指标值之和，对应基质渗透率的K3值即为0.005mD的指标值之和，对应人工裂缝长度的K3值即为缝长为250m的指标值之和，kl至k5为Kl至K5的平均值。R表示极差，即Max(Ki) －Min(Ki)，i=l，2，3，4，5。

由表4可以看出，从极差R值大小来看，基质渗透率最大，人工裂缝长度次之，天然裂缝间距再次，气体吸附比最小。也就是说，以上4个参数值改变相同幅度时，10年累计产气量对基质渗透率的变化最为敏感。可以认为，以10年累计产气量为指标时，影响因素的主次顺序为基质渗透率、人工裂缝长度、天然裂缝间距和气体吸附比。

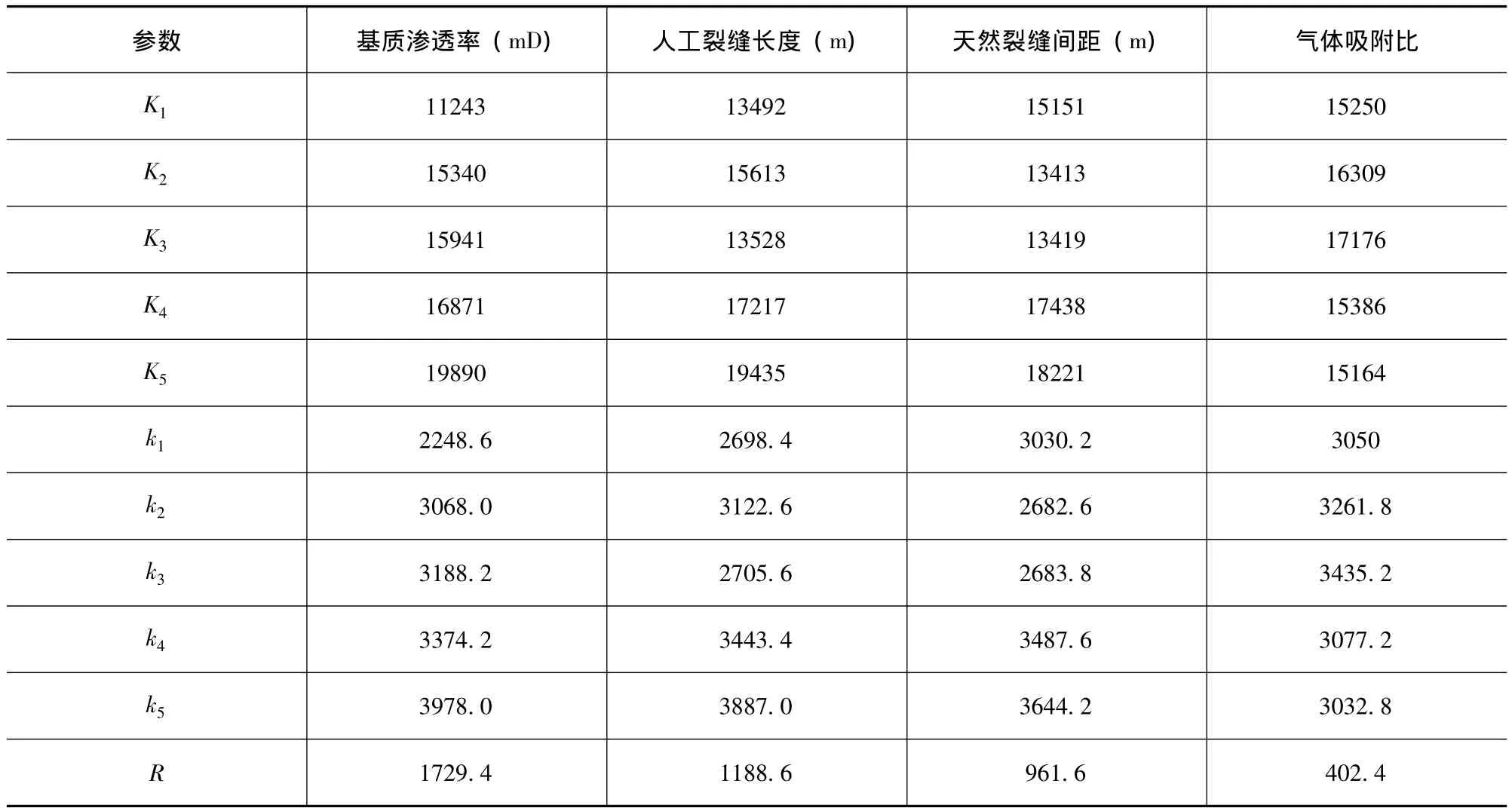
表4 极差分析表Table 4 Range analysis table

4.3 层次分析法

层次分析法是将与决策有关的元素分解成多个层次，在此基础上进行定性和定量分析。层次分析法建模基本上可以分为以下4个步骤。

4.3.1 建立递阶层次结构模型

分为最高层、中间层和最底层。最高层，即是预定的指标，本例中就是10年累计产气量;中间层，包含了实现目标所涉及的中间环节，即基质渗透率、人工裂缝长度、天然裂缝间距和气体吸附比;最底层，包括了实现目标的具体措施和方案。

4.3.2 构造各层次中的所有判断矩阵

由于进行比较的因素多，所以提出一种因子两两比较的方案，即每次取两个因子xi和xj，以aij表示xi和xj对z的影响大小之比，结果用矩阵A=(aij)n×n表示，称A为z—x之间的成对比较判断矩阵。可以看出，若xi拜口xj对z的影响之比为aij，则xi墨和xj对z的影响之比应为aij=1/aij。

关于如何确定aij的值，建议引用数字1～9及其倒数作为标度。表5列出了1～9标度的含义。

表5 9标度法表Table 5 Nine scale analysis method

4.3.3 层次单排序及一致性检验

通过以上成对比较之后，虽然能一定程度上减少其他因素的干扰，但是仍然会客观存在一定的非一致性，因此需要进行一致性检验，检验过程可查阅相关参考文献［24～26］。

4.3.4 层次总排序及一致性检验

以上得到了一组元素对上一层元素的权重向量，最终还需要得到最底层各元素对目标层的排序权重，从而进行方案选择，层次总排序就是自上而下对单排序的权重进行合成［27～31］。

以10年累计产气量为目标层，以基质渗透率、人工裂缝长度、天然裂缝间距和气体吸附比为准备层，判断准备层对目标层的排序。实验总结得出，基质渗透率的权重占到43%，对产能的影响最大;人工裂缝长度次之，权重为25%;天然裂缝间距再次，权重为13%;气体吸附比最小，权重为13%。

4.4 BP试验法

PlackettBurman试验 (BP试验)，实际上就是一种筛选试验，它是对于试验次数多，且没有明确了解各因素对指标的影响强弱次序的情况下采用的一种试验设计方法。此方法对每个因子取两水平来进行分析，通过比较各个因子两水平的差异与整体的差异来确定因子的显著性。图6a“+”表示最大值，“－”表示最小值，字母A至G表示不同的因素。本例中，只用A至D范围内的表，E至G的表删除即可。此方法为定性分析方法，所选指标为10年累计产气量。图6b为4个参数对指标的敏感程度，从图中可以看出，基质渗透率和人工裂缝长度对页岩气藏单井产能的影响较为显著，而天然裂缝间距和气体吸附比对产能的影响不是很显著。

图6 BP试验设计表和各参数对指标的敏感程度图Fig.6 BP test design table and sensibility degree for different parameters

综合以上分析可以看出，页岩储层的基质渗透率对产能的影响最为显著，然而对于指定的页岩储层，基质渗透率变化幅度比较小，因此若要实现较好的开发效果，人工改造规模就显得非常重要。另外，天然裂缝的发育程度也是影响产能的一个很重要的因素。总之，对于指定的页岩储层，在基质渗透率和天然裂缝发育程度固定的情况下，应尽可能地增加人工改造的力度，尽最大可能增加改造体积，实现对页岩气藏的较好开发。

为了能够得到任意参数组合下的改造体积形状和大小，本文通过建立BP人工神经网络模型对这一问题进行了研究。BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出的，是一种误差逆传播算法训练的多层前馈网络，它是对人脑或自然神经网络若干基本特性的抽象和模拟，是目前应用最广泛的神经网络模型之一。BP网络模型由3个层组成:输入层、输出层和隐含层，其中隐含层可以是一层或多层，每层由多个神经元组成 (图7)。BP网络模型多层前馈网络的算法可简述如下。

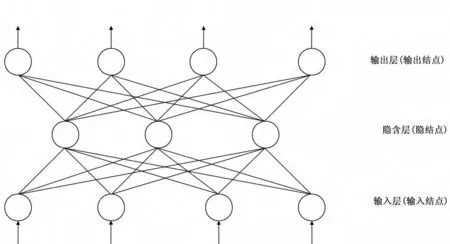
图7 BP神经网络模型结构图Fig.7 BP artificial neural network model

(1)假设:

①输入层有m0个神经元;

②网络有n层，输出层为第n层，第k层有mk个神经元;

③uk(i)表示第k层第i个神经元所接受的信息，wk(i，j)表示第k－1层第j个神经元到第k层第i个神经元的权重，ak(i)表示第k层第i个神经元的输出，ao(j)表示输入的第j个分量;

④层与层之间的神经元存在信息交换，但同一层之间的神经元无信息交换;

⑤信息交换的方向是从输入层到输出层方向，没有反向信息传播。

(2)根据以上假设，网络的输入、输出关系可表示为:

(3)对于具有多个隐含层的前馈神经网络，若激发函数为 S，即:f(x)=1/［1+exp(－x)］，且指标函数取:

其中:

(4)权重迭代公式为:

然后选定学习的数据，随机确定初始权矩阵，用学习数据计算网格输出，再根据上述公式进行反向修正，直到用完所有学习数据。BP网络建模具有非线性映照能力、并行分布处理方式、自学习和自适应能力、数据融合的能力和多变量系统等特点，是一种成功的模拟方法。

结合本文的目的，确定了采用BP网络模型来解决改造面积形状和大小为目标函数的问题。用上述模拟实验的结果为例，采用基质渗透率、人工裂缝长度和天然裂缝间距与改造面积形状和大小一一对应的数据输入模式，应用MATLAB语言进行了建模和计算。

在BP网络模型对改造面积长宽比和改造面积长边长的训练中对改造面积长宽比的训练次数达到261次，最终误差为0.00095;对改造面积长边长的训练次数为239次，最终误差为0.00099;由此可见，BP网络模型通过大量的训练对数值模拟结果实现很好的逼近 (图8)。综上所述，可以通过大量的数值模拟结果和BP网络模型训练相结合的方法预测出不同基质渗透率、人工裂缝长度和天然裂缝间距条件下改造面积的形状和大小。

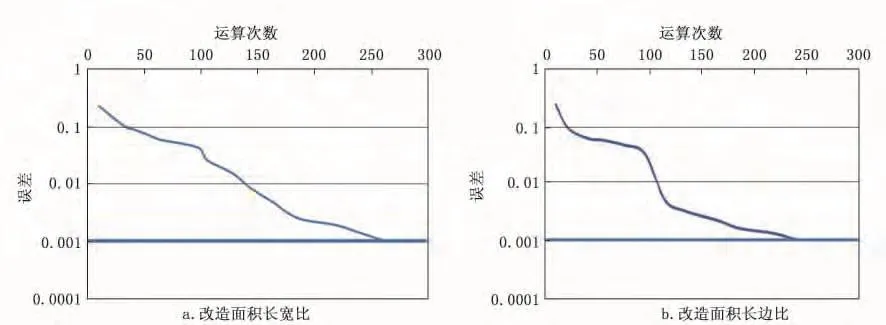
图8 BP网络模型对改造面积长宽比和长边长的训练结果图Fig.8 Exercise results for stimulated area length－wide ratio and area side length with BP network model

5 结 论

通过大量数值模拟对影响页岩气藏单井产能的因素进行分析，包括基质渗透率、人工裂缝参数、天然裂缝参数及气体吸附比等，结果表明:

(1)随着基质渗透率、人工裂缝长度、人工裂缝条数、气体吸附比增加及天然裂缝间距减小，单井产能增加，反之亦然。

(2)通过正交试验方法得到了各因素对产能影响的主次关系，并采用层次分析法和BP试验法对该关系进行了验证，得出对产能影响最大的3个因素为基质渗透率、人工裂缝长度和天然裂缝间距。

(3)以上述3个因素为变量，通过大量的模拟计算绘制了图版，建立了BP网络模型对图版数据进行了训练，用以快速确定任意条件下的改造体积形状和大小。

［1］邹才能，董大忠，杨桦，等.中国页岩气形成条件及勘探实践［J］.天然气工业，2011，31(12):26－39．

［2］张林晔，李政，朱日房.页岩气的形成与开发 ［J］．天然气工业，2009，29(1):124－128.

［3］聂海宽，何发岐，包书景.中国页岩气地质特殊性及其探对策 ［J］．天然气工业，2011，31(11):111－116.

［4］孟庆峰，侯贵廷.阿巴拉契业盆地Marcellus页岩气藏地质特征及启示 ［J］.中国石油勘探，2012，17(1):67－73.

［5］刘成均，郭平，蒙春，等.页岩气开发利用及其前景分析 ［J］.石油科技论坛，2014，33(2):40－46．

［6］刘存忠.页岩气开发现状及前景思考 ［J］．石油科技论坛，2013，32(3):32－37．

［7］张焕芝，何艳青.全球页岩气资源潜力及开发现状［J］.石油科技论坛，2010，29(6):53－57．

［8］张抗，页岩气革命带来油气地质学和勘探学的重大创新 ［J］．石油科技论坛，2012，31(6):37－41．

［9］杨金华，田洪亮，郭晓霞，等，美国页岩气水平井钻井提速提效案例与启示 ［J］．石油科技论坛，2013，32(6):44－48．

［10］陈桂华，祝彦贺，徐强.页岩气成藏的四性特征及对下扬子地区页岩气勘探的启示 ［J］．中国石油勘探，2012，17(5):63－70．

［11］张金川，金之钧，袁明生.页岩气成藏机理和分布［J］．大然气工业，2004，24(7):15－18．

［12］蒋裕强，董大忠，漆麟，等.页岩气储层的荩本特征及其评价 ［J］．天然气工业，2010，30(10):7－12．

［13］张金川，姜生玲，唐玄，等.我国页岩气富集类型及资源特点 ［J］．天然气工业，2009，29(12):109－114．

［14］张金川，汪宗余，聂海宽，等.页岩气及其勘探研究意义 ［J］．现代地质，2008，(4):640－646.

［15］李欣，段胜楷，孙扬，等.美国页岩气勘探开发最新进展 ［J］．天然气工业，2011，(8):124－126，142．

［16］于荣泽，张晓伟，卞亚南，等.页岩气藏流动机理与产能影响因素分析 ［J］．天然气工业，2012，(9):10－15，126．

［17］程远方，董丙响，时贤，等，页岩气藏三孔双渗模型的渗流机理 ［J］.天然气工业，2012，32(9):44 －47，130．

［18］谢维扬，李晓平.水力压裂缝导流的页岩气藏水平井稳产能力研究［J］．天然气地球科学，2012，23(2):387－392．

［19］王永辉，卢拥军，李永平，等.非常规储层压裂改造技术进展及应用 ［J］．石油学报，2012，33(增刊):149－158．

［20］Durbin P A，Iaccarino G．An approach to local refinement of structured grids［J］．Journal of Computational Physics，2002，181:639－653．

［21］Mehl S，Hill M C，Leake S A．Comparison of local grid refinement methods for Modflow ［J］．Ground Water，2006，44(6):792－796．

［22］Kilic A，Ertekin T．Application or a local grid refinement protocol in highly faultcd rescrvoir architectures ［J］．Journal of Canadian petroleum technology，2003，42(4):58－69．

［23］Shaoul J R，Behr A，Mtshedlishvili G．Developing a tool for 3D reservoir simulation of hydraulically fractured wells．IPTC10182，2005．

［24］景龙华，基于AHP的企业现金流量分析 ［J］．现代商贸工业，2010，22(9):182－183.

［25］郭金玉，张忠彬，孙庆云.层次分析法的研究与应用［J］.中国安全科学学报，2008，18(5):148－153．

［26］邓雪，李家铭，曾浩健，等.层次分析法权重计算方法分析及其应用研究 ［J］．数学的实践与认识，2012，42(7):93－100．

［27］郭金玉，张忠彬，孙庆云.层次分析法的研究与应用［J］.中国安全科学学报，2008，18(5):148－153．

［28］邓雪，李家铭，曾浩健，等.层次分析法权重计算方法分析及其应用研究 ［J］．数学的实践与认识，2012，42(7):93－100．

［29］杨莉娜，杨斌，鲁洪江，等.五百梯气田长兴组储层裂缝发育程度的常规测井神经网络预测 ［J］．中国石油勘探，2011，16(1):63－69．

［30］甘云雁，张士诚，陈利，等，复杂断块油藏不规则井网整体压裂优化设讣 ［J］.石油学报，2006，27(4):81－84.

［31］Rumelhart D E，McCelland J L．Parallel distribution processing(Vols I and II)［M］.Cambridge:MIT Press，1986．