考虑多种效应的致密气藏不对称裂缝井产能模型
2014-12-13姚健欢
姚健欢
(中国石油大学 (北京)石油工程教育部重点实验室,北京 102249)
致密气藏储层孔渗低,受到启动压力梯度、应力敏感效应、滑脱效应等综合影响,气井不经改造则产能低甚至无产能,经储层改造后增大气井与储层接触面积,加大流体的流动能力,从而获得经济产能[1-2]。应力分布不均匀的储层改造后会形成形状不规则的非对称裂缝,因此,对应力不均匀的致密气井进行压裂产能研究具有重要意义。
目前针对对称压裂气井,考虑启动压力梯度、应力敏感、滑脱效应等多种因素综合影响下的产能预测模型研究较多[3-6]。王志平[3]等将渗流区域分为3区,建立了考虑3种因素影响下的压裂气井产能模型;张强[4]等建立了考虑高速非达西效应的渗流模型;李勇明等[5]考虑气、水两相流动,研制相应数值模拟软件;牟松茹等[6]通过实验和数值模拟方法,研究了启动压力梯度对致密气藏的影响。
现今研究中针对非对称裂缝的研究较少,利用保角变换原理,彭昱强[7]等推导出不完全对称多水平井的产能公式及渗流场分布;郑松青[8]建立非均匀压裂水平井产能模型;曹宝军[9]等将其应用到不对称双垂直压裂气井产能计算;熊健[10,11]等先后推导出不对称垂直压裂油、气井的产能数学预测模型,并分析了启动压力梯度及导流能力等因素的敏感性。但上述模型均没有综合考虑多种因素的影响,因此本文建立了考虑多种因素影响下的不对称压裂气井产能预测模型,并分析相关参数敏感性,旨在推动致密气井不对称压裂研究。
1 产能公式推导
假设条件:储层恒温、水平、均质、等厚、各向同性;裂缝两翼对称,缝高贯穿整个储层,缝宽忽略不计;储层单相气体符合线性渗流规律;渗流过程稳定,裂缝无限导流,考虑应力敏感和启动压力梯度、滑脱效应的影响。
Klinkenberg指出在多孔介质中,气体存在滑脱效应,气体渗透率K与绝对渗透率K0存在特定关系式:
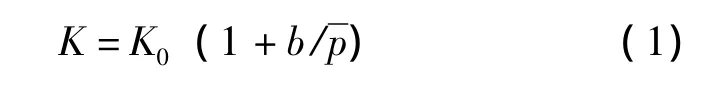
式中 b——滑脱因子,MPa;
对于裂缝发育的致密储层,气体渗透率与有效应力呈指数关系:

式中 α——应力敏感系数,MPa-1;
pe——原始地层压力,MPa;
p——目前地层压力,MPa。
气体在孔喉中渗流时,需克服水化膜的渗流阻力,因此其运动方程为:

式中 v——渗流速度,m/s;
μ——气体黏度,mPa·s;
λ——阈压梯度,MPa/m;
r——水化膜半径,m。
双裂缝不对称压裂井指:裂缝对称分布,但两条裂缝长度不等,较长裂缝半长为L2而较短裂缝半长为L1。针对图1水力压裂后形成的具有不对称压裂井的地层,利用保角变换原理将此复杂渗流情况转换为简单渗流情况,取变换函数z[5]:

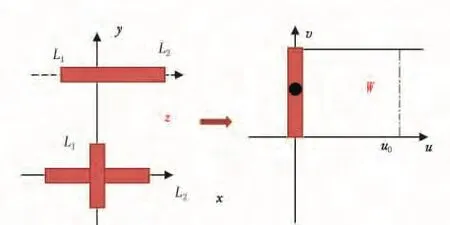
图1 坐标变换示意图Fig.1 Coordinate transformation diagram

式中 shu——双曲正弦函数;
chu——双曲余弦函数。
使式 (5)实部和虚部对应相等,可得坐标对应关系:

根据式 (6)、式 (7),可得流线和等势线方程:

在W平面u轴上u0较大 (即对应z平面供给边界),根据chu≈shu,则可得:
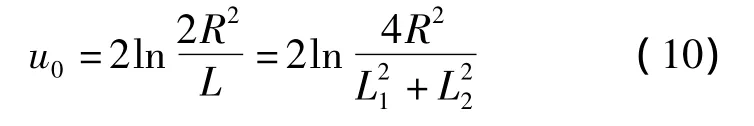
式中 u0——u轴上较远点;
R——供给半径,m。
通过上述变换将图1复杂渗流转换为一维排液坑道渗流,保角变换前后,不同空间的产能相等,因此多裂缝不对称压裂气井产量可由一维排液坑道产量表示,并将地下产量换算到地面标准状态下:
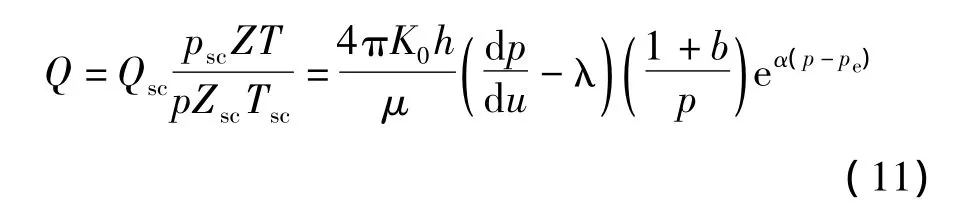
式中 Q、Qsc——储层和标况下流量,m3/d;
psc——标准状态下压力,MPa;
Zsc——标准状态下气体压缩因子;
Tsc——标准状态下温度,K;
h——储层厚度,m;
pe、pw——原始地层压力与气井井底流压,MPa;
H(pe)、H(pw)——供给边界、井底处压力函数。
定义函数:

引入拟压力:

可得:
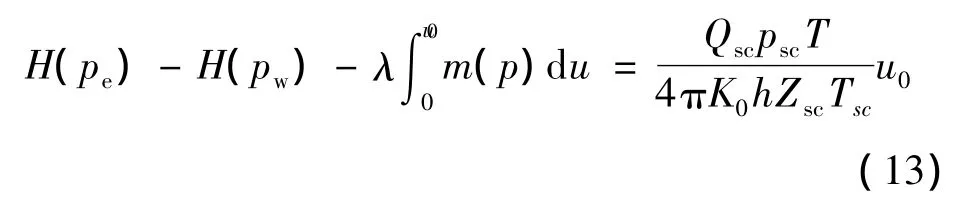
上式即为考虑启动压力梯度、应力敏感系数及滑脱效应在内的多裂缝非对称压裂井产能预测公式。
为简化上述模型,假设压缩因子和气体黏度的乘积为常数,且物性参数通过平均压力求取。则可简化考虑多种因素的多裂缝不对称压裂井产能方程:
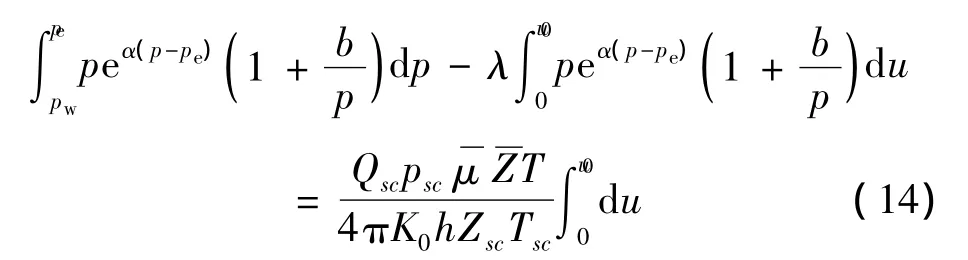
采用气田实际使用单位,取地层平均压力:p=(pe+pw)/2,且 Tsc=293K,psc=0.1MPa,定义裂缝非对称率δ=L2/L1表征多裂缝不对称程度,则可得到简化后公式:

其中:
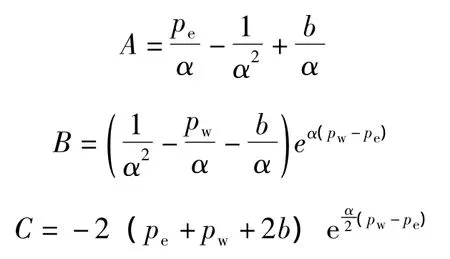
若不考虑启动压力梯度、应力敏感及滑脱效应等的影响,可得到多裂缝不对称压裂气井产能方程:

利用相同变换原理和方法,可得考虑启动压力、应力敏感、滑脱效应综合影响下,单裂缝不对称垂直压裂气井产能公式:

2 实例分析
国内某致密气田X井基本参数为:储层有效厚度11.6m、原始地层压力30.5MPa、储层温度为364.2K,气体平均压缩因子0.854、气体平均黏度0.017mPa·s、储层原始渗透率0.241mD、供给半径488m;岩心实验表明,气体启动压力梯度为0.002MPa/m;围压实验测得:其应力敏感系数0.021MPa-1、滑脱因子2MPa。致密储层改造效果较理想,形成垂直产状裂缝,裂缝半长均为134.8m。该垂直裂缝气井系统试井后测得其绝对无阻流量为11.34×104m3/d,根据公式计算得到的绝对无阻流量 10.65×104m3/d、相对误差6.08%,符合工程精度。
3 不对称裂缝产能分析
某致密压裂气井参数:储层原始地层压力为32MPa,储层温度为363K,有效厚度为22.8m,供给半径为450m,气井半径为0.1m,克氏渗透率为0.167mD,气体黏度为0.0224mPa·s,气体平均压缩因子为0.868,孔隙度为1.2%,应力敏感系数为0.018MPa-1,启动压力梯度为0.007MPa/m,滑脱因子为1.8MPa,双裂缝井裂缝半长分别为120m和100m。
利用Matlab编制计算程序,采用控制变量法分别研究式 (15)不同参数变化程度对气井产能影响。启动压力梯度分别为0MPa/m、0.004MPa/m、0.006MPa/m、0.008MPa/m、0.01MPa/m;应力敏感系数分别为0MPa-1、0.02MPa-1、0.04MPa-1、0.06MPa-1、0.08MPa-1;滑脱因子分别为0MPa、1MPa、2MPa、3MPa、4MPa;裂缝非对称率分别为1、1.5、2、2.5、3。
由不对称压裂气井绝对无阻流量随启动压力梯度变化曲线 (图2)可知,随着启动压力梯度增大,流体流动需要克服更大的阻力,不对称压裂气井绝对无阻流量逐渐降低;当启动压力梯度分别为 0.004MPa/m、0.006MPa/m、0.008MPa/m、0.01MPa/m时,不对称压裂气井绝对无阻流量与不考虑启动压力影响时分别相对减小0.079%、0.119%、0.158%、0.198%,虽然气井产能随着启动压力梯度增大而降低,但影响幅度很小。

图2 启动压力梯度对气井绝对无阻流量影响图Fig.2 Impact of threshold pressure gradient on absolute open flow capacity
由气井流入动态曲线与应力敏感系数关系(图3)可知,当应力敏感系数分别为0.02MPa-1、0.04MPa-1、0.06MPa-1、0.08MPa-1时,与 不 考虑应力敏感性情况下相比气井无阻流量相对降低10.3%、19%、26.59%、35%。即随着应力敏感系数的增大,气井产能降低幅度较大;但随着应力敏感系数的持续增大,气井产能降幅减小,这是因为生产压差增大过程中,储层岩石孔隙、喉道不断压实减小,当其形变到一定程度后,其可变化空间大大缩小。

图3 应力敏感系数对气井IPR曲线影响图Fig.3 Impact of stress sensitivity coefficient on gas well IPR curve
由图4可知随着滑脱因子的增大,气井产量逐渐增大,当滑脱因子分别为 1MPa、2MPa、3MPa、4MPa时,气井绝对无阻流量相对增加5.7%、11.4%、17.1%、22.8%;这主要因为气体在岩石孔道内无吸附层;当压力较低时,气体分子的平均自由路程达到孔道尺寸,气体分子扩散不碰撞自由运动,导致视渗透率增加。且井底流压逐渐降低过程中,滑脱因子对气井产能影响幅度逐渐增大。
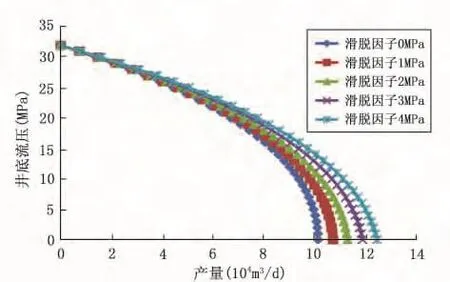
图4 滑脱效应对气井IPR曲线影响图Fig.4 Impact of slippage effect on gas well IPR curve
在压裂裂缝总长度不变的条件下,对于单裂缝不对称压裂气井,由式 (17)可知,裂缝非对称率对气井产能无影响。而对于双裂缝不对称压裂气井,裂缝对气井产能产生一定影响。由图5可知,当裂缝非对称率分别为1.5、2、2.5、3时,气井绝对无阻流量与裂缝对称 (非对称率为1)时相比提高1.38%、3.79%、6.19%、8.37%。即在双裂缝总长度一定情况下,气井产能随着裂缝不对称程度的加大而逐渐增大。
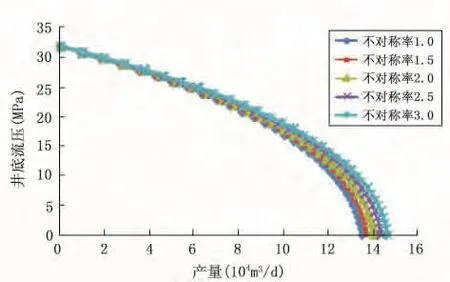
图5 非对称率对气井IPR影响图Fig.5 Impact of fracture asymmetry index on gas well IPR curve
综上所述,对于双裂缝非对称压裂致密气井,启动压力梯度、应力敏感系数、滑脱效应及裂缝非对称率对气井产能影响程度不尽相同;且由上述分析可见,启动压力梯度对产能影响幅度最弱,其次为裂缝非对称率、滑脱效应,而应力敏感系数对产能影响最大。
4 结 论
(1)基于稳定渗流理论,利用保角变换原理,推导了考虑启动压力梯度、应力敏感效应、滑脱效应在内的不对称单裂缝、双裂缝压裂致密气井产能预测公式,引入非对称率概念,并对各影响因素进行敏感性分析,对压裂致密气井产能预测有一定实际意义。
(2)气井实际生产过程中,随着启动压力梯度和应力敏感系数的增大,气井产能降低;随着滑脱效应和裂缝非对称率的增大,气井产能增大;启动压力梯度对气井产能影响最弱,其次为裂缝非对称率,再次为滑脱效应;应力敏感对气井产能影响最大;对于应力敏感性强的储层,建议采用定压差生产工作模式。
[1]赵继勇,刘振旺,谢启超,等.鄂尔多斯盆地姬塬油田长7致密油储层微观孔喉结构分类特征 [J].中国石油勘探,2014,19(5):73-79.
[2]张威,刘新,张玉玮.世界致密油及其勘探开发现状 [J].石油科技论坛,2013,32(1):47-50.
[3]王志平,冉启全,童敏,等.致密气藏压裂气井产能计算新方法 [J].科学技术与工程,2013,13(36):10806-10810.
[4]张强,王永清,张楠,等.低渗透应力敏感气藏压裂井产能分析 [J].特种油气藏,2012,19(3):74-76,154.
[5]李勇明,郭建春,赵金洲.压裂气井产能模拟研究[J].钻采工艺,2002,25(1):40-43.
[6]牟松茹,张士诚,张平.考虑启动压力梯度的致密气藏压裂井产能分析 [J].科学技术与工程,2011,11(34):8434-8437.
[7]彭昱强,何顺利,魏俊之.不完全对称多井底水平井产能研究 [J].大庆石油地质与开发,2003,22(2):28-30,86.
[8]郑松青.非均匀分段压裂水平井产能计算 [J].大庆石油学院学报,2013,(4):55-59,121.
[9]曹宝军,李相方,姜子杰,等.压裂火山岩气井不对称裂缝产能模型研究[J].天然气工业,2009,29(8):79-81,141-142.
[10]熊健,王小军,吕雷.低渗油藏不对称垂直裂缝井产能模型 [J].科技导报,2013,22:40-43.
[11]熊健,刘海上,赵长虹,等.低渗透气藏不对称垂直裂缝井产能预测 [J].油气地质与采收率,2013,20(6):76-79.
