焊接结构多轴疲劳寿命预测结构应力法

刘 刚，刘英芳，黄 一

（大连理工大学 船舶工程学院，辽宁 大连116024）

1 引 言

焊接结构在海洋工程领域有着非常广泛的应用，由于风、浪、流的交互作用，结构内部通常会出现局部应力集中现象，而该应力集中位置的应力状态一般是多轴交变的，通常在焊趾位置会萌生疲劳裂纹，进而导致结构的疲劳破坏。不同于单轴疲劳问题，海洋工程焊接结构的多轴疲劳破坏主要是由随机波浪载荷、复杂结构形式、不同裂纹萌生方向以及焊接残余应力导致[1-2]。然而在海洋工程领域，对焊接结构的多轴疲劳寿命研究较少，人们主要采用单轴疲劳寿命预测理论对焊接结构进行保守的疲劳寿命预测，导致疲劳寿命预测结果分散性较大[3-4]。

为了能够提高焊接结构疲劳寿命预测的准确性，本文提出了一种评估焊接接头疲劳强度的新型结构应力法，与临界面理论相结合，建立了一种能够用于实际焊接结构的多轴疲劳寿命预测方法。和传统的热点应力法不同，新型结构应力法的应力评估点不是在结构表面，而是在板厚方向选取结构内部一点。该方法一方面在一定程度上考虑了应力梯度对疲劳强度的影响，比传统的热点应力法更准确；另一方面评估点的应力状态可以直接通过有限元计算获得，便于和多轴疲劳的临界面理论相结合，实现复杂焊接结构的多轴疲劳寿命预测。

本文首先提出了新型零点结构应力的定义，并讨论了零点位置的变化规律和计算方法；然后利用公开发表的疲劳试验数据，通过有限元分析验证了零点结构应力法的准确性；其次联合临界面理论验证了利用零点结构应力法进行多轴疲劳寿命预测的可行性和精度；最后将本文提出的方法应用于海洋工程管节点的多轴疲劳强度评估。

2 零点结构应力定义

如图1（a）和（b）所示，在焊趾处A点，垂直于焊缝方向的切口应力σln可分解为膜应力σm、弯曲应力σb和非线性应力峰值σnlp，其大小可根据板厚方向（x方向）的应力分布 σx计算得到，如（1）-（3）式所示[5]，式中t为板厚。

分析焊趾处在板厚方向的切口应力场，除了需要满足本构方程外还应满足平衡方程和协调方程。已知切口应力可分解为结构应力（膜应力和弯曲应力）和非线性分布应力两种不同性质的应力分布，其中结构应力具有平衡外加载荷的作用，满足平衡方程，非线性分布应力由焊趾引起，具有自平衡特性，满足变形协调方程。既然非线性分布应力在板厚方向处于自平衡状态，必然会在靠近板材表面下的一点处应力值变为零，作者提出非线性分布应力为零的位置作为焊接接头的疲劳评估点，称该点为零点。该点的总体应力中不包含非线性分布应力，只包含结构应力，因此称为零点结构应力。关于零点位置的确定，可以在通过有限元计算获得σ（x）的情况下，令（3）式中的非线性分布应力σnlp（x）为零，直接求得零点位置到板表面的距离。

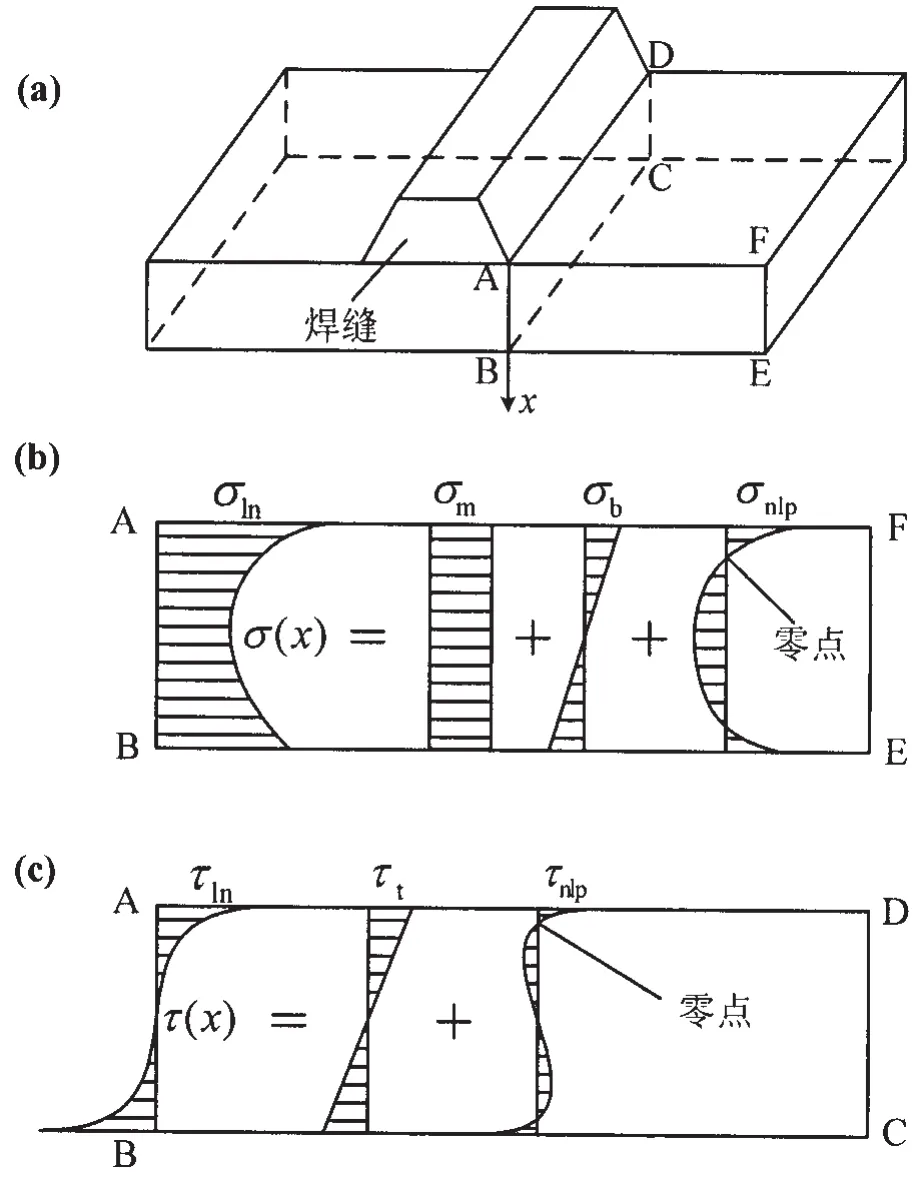
图1 热点处板厚方向典型的非线性应力分布Fig.1 Typical nonlinear stress distribution at hot spot

当焊接接头受到拉伸载荷时，板厚方向只有膜应力σm，此时零点结构应力与表面的热点应力值相等；当受到弯曲载荷时，由于弯曲应力沿板厚方向的分布具有应力梯度，故零点结构应力略小于表面的热点应力，在一定程度上能够考虑应力梯度对疲劳强度的影响。

在焊趾处A点的应力分量中，除了垂直于焊缝方向的正应力外，还存在两个方向的剪应力。一是板厚方向的剪应力，因其在板表面附近接近于零可以忽略不计；二是平行于焊缝方向的剪应力，如图1（c）所示，该剪应力和弯曲正应力具有相同的分布形式，因此与（2）式和（3）式相似，其零点位置可以通过以下两式计算：

式中：σm为板表面的剪应力，τ（x）为板厚方向的剪应力分布。

3 零点位置计算

为了计算零点结构应力，首先要确定零点位置。以对接焊缝作为研究对象，材料为普通钢，弹性模量为210 GPa，泊松比为0.3。几何参数如图2所示，其中t为板厚，h为焊腿高度，d为零点距离平板表面深度，θ为焊趾角度，r为焊趾端部圆弧半径。图3为采用8节点六面体单元建立的有限元模型，在焊趾附近网格尺寸设置为0.01t。经过验证，该网格大小保证了计算结果具有足够的精度。

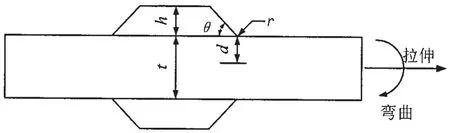
图2 对接焊缝几何参数Fig.2 Geometric parameters of a butt joint

图3 对接焊缝有限元模型Fig.3 Finite element model of the butt joint

表1 对接焊缝几何参数取值范围Tab.1 Ranges of the geometric parameters of the butt joint

模型板厚t为20 mm，焊趾尺寸所取参数如表1所示。为了便于分析，本文将零点位置全部归一化表示为d/t。

定义ρ为载荷比例系数，表示不同的拉弯组合工况，如（6）式所示。这里 σm+σb≠0，即不考虑板表面合应力为零的情况。σm和σb可能同为拉应力或者同为压应力，也可能一个是拉应力而另一个是压应力。根据不同的受力状态，ρ的变化范围如（7）式所示。计算中选取了38种不同载荷组合工况（见表2）进行零点位置计算。

依据表1和表2，对不同几何参数的平板对接焊缝，计算不同载荷工况作用下的零点位置，计算结果如图4所示。图中的垂线实际上是多个表示零点位置的点的集合。从零点位置的分布可以看出，在相同的载荷工况下，零点位置受到焊趾尺寸的影响而在一定范围内变化。为了便于工程应用，本文忽略焊趾尺寸对零点位置的影响，对所得到的零点位置进行数据拟合，即在相同的载荷工况下，只取拟合点的数据作为零点位置。拟合得到的分布函数如（8）式和图4所示。

式中：a=0.068 33，b=0.063 74。

对于纯扭转加载情况，剪应力的零点位置变化规律与纯弯曲加载时的规律几乎一致，因此扭转工况下剪应力零点位置的确定可以按照纯弯曲加载情况处理，载荷比例系数取ρ=0。

图4 零点位置数值计算结果及其拟合分布函数Fig.4 Numerical results of the zero point and their fitting distribution functions

表2 拉弯组合载荷工况Tab.2 Loading cases of combined tension and bending

4 零点结构应力法精度验证

为验证本文方法，作者收集了多篇国际公开发表的焊接结构疲劳实验数据[6-12]，有限元模型如图5所示。其中除试件（b）以外的所有试件均为角焊缝，承受单轴拉伸和弯曲载荷时所对应的热点应力S-N曲线均为FAT90。将这5个试件在弯曲和拉伸作用下的疲劳实验数据集中在一起，如图6所示，空心圆圈表示热点应力HSS，实心方块表示由本文方法计算得到的零点结构应力ZPSS。

将实验数据以反向斜率m=3.0拟合，得到热点应力表示的疲劳数据平均曲线（Mean of HSS）和零点结构应力表示的疲劳数据平均曲线（Mean of ZPSS）。为了比较，同时将标准S-N曲线FAT90和生存概率50%的FAT90平均曲线也表示在图中。

图5 焊接试件有限元模型Fig.5 Finite element models of welded specimens

由图6可以看出，由于多数焊接试件受到弯曲载荷作用，零点结构应力的数据点多数位于热点应力数据下方，说明本文方法可以考虑由弯曲引起的板厚方向应力梯度对疲劳强度的影响。另外对比零点结构应力平均曲线（Mean of ZPSS）、热点应力平均曲线（Mean of HSS）和FAT90平均曲线，可以看出零点结构应力平均曲线更接近于FAT90平均曲线，说明零点结构应力计算结果比传统的热点应力更加准确。

图6 分别使用热点应力和零点结构应力表示的疲劳实验数据Fig.6 Fatigue data shown by the HSS and ZPSS

5 零点结构应力法的多轴疲劳寿命预测验证

零点结构应力直接由有限元计算结果后处理获得，因此可与多轴疲劳准则联合进行寿命预测。作者采用由Susmel提出的多轴疲劳寿命评估方法MWCM法[13]，对零点结构应力法的可行性进行验证。

MWCM法是一种基于临界面理论的多轴疲劳寿命预测方法，在多轴疲劳寿命预测方面具有较高精度。MWCM法使用标准拉伸S-N曲线和扭转S-N曲线确定其控制方程如（9）和（10）式所示，其中ρw=△σn/△τ，在确定临界面上的最大剪切应力范围 之后，可由（11）式计算疲劳寿命，具体计算过程见文献[14]。

对于图5所示的焊接试件，分别应用本文方法和热点应力法联合MWCM法进行多轴疲劳寿命预测。多轴疲劳载荷数据分为比例载荷和非比例载荷两类，将预测结果表示在图7所示的双对数精度验证图中，横轴为预测寿命，纵轴为疲劳试验获得的寿命，并分别标出±100%和±300%误差带。由结果可以看出，零点结构应力法的多轴疲劳寿命预测效果整体上要优于热点应力法的预测结果，尤其是对于非比例载荷预测精度的提高更为显著。研究非比例载荷情况下MWCM法的ρw值发现，零点结构应力法计算得到的ρw值要小于热点应力法，导致MWCM法反向斜率k的增大，进而使零点结构应力法的预测寿命大于热点应力法的预测寿命。

图7 MWCM法分别联合（a）零点结构应力法和（b）热点应力法的多轴疲劳寿命预测精度Fig.7 Accuracy of the MWCM applied in terms of(a)ZPSS and(b)HSS

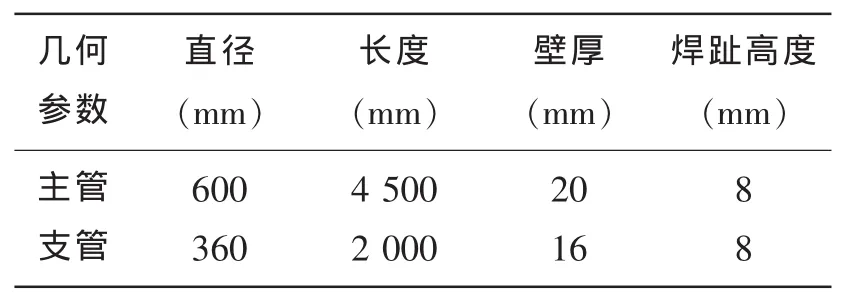
表3 管节点几何尺寸Tab.3 Geometries of the tubular T-Joint

图8 T型管节点有限元模型Fig.8 Finite element model of a T-joint

6 零点结构应力法在管节点多轴疲劳寿命预测中的应用

本文选取海洋工程中典型T型焊接管节点作为研究对象，如图8所示，支管端部受到弯曲载荷B和拉伸载荷F共同作用。T 型管节点的几何尺寸见表3。选择支管冠点作为疲劳评估点，使用零点结构应力法联合MWCM计算该点在不同载荷作用下的多轴疲劳寿命，具体载荷信息及疲劳寿命预测结果见表4。载荷工况包括纯弯曲、纯拉伸、同相及非比例载荷四种，其中工况1-4的外加载荷平均应力为零，工况5-8的外加载荷平均应力不为零。对比预测结果，可以看出工况5-8的预测寿命分别要比工况1-4的预测寿命低，表明平均应力对焊接试件疲劳寿命是不利的；而对比工况3、7和工况4、8的预测寿命，工况4的预测寿命要高于工况3，工况8的预测寿命高于工况7，表明外加载荷的相位差对疲劳寿命的影响并不总是有害，这与一些文献[8,15]中的实验现象是一致的。

表4 载荷信息及疲劳寿命预测结果Tab.4 Loading cases and estimated results of the fatigue life

7 结 论

（1）本文提出了一种新型结构应力法，该方法以焊趾处板厚方向非线性分布应力为零位置的结构应力作为评估应力，在一定程度上能够考虑应力梯度对疲劳寿命的影响，比传统的热点应力法具有更高的精度。

（2）零点结构应力可以直接由有限元计算结果后处理得到，因此零点结构应力法可以联合多轴疲劳准则MWCM法进行寿命预测。通过对一系列国外已发表的疲劳试验数据进行有限元分析表明，在进行多轴疲劳寿命预测时零点结构应力法同样比传统热点应力法具有更高精度，在结构受到非比例载荷作用时尤为明显。

（3）零点结构应力法可以用于实际海洋工程复杂焊接结构的多轴疲劳寿命预测。

[1]Liu Y,Mahadevan S.Multiaxial high-cycle fatigue criterion and life prediction for metals[J].International Journal of Fatigue,2005,27(7):790-800.

[2]Susmel L.Modified Wöhler curve method,theory of critical distances and Eurocode 3:A novel engineering procedure to predict the lifetime of steel welded joints subjected to both uniaxial and multiaxial fatigue loading[J].International Journal of Fatigue,2008,30(5):888-907.

[3]Partanen T,Niemi E.Hot spot stress approach to fatigue strength analysis of welded components:Fatigue test data for steel plate thicknesses up to 10 mm[J].Fatigue&Fracture of Engineering Materials&Structures,1996,19(6):709-722.

[4]Anon.Eurocode 3-Design of steel structures-part 1-1:General rules and rules for buildings[M].DD ENV 1993-1-1:1992.

[5]Hobbacher A.Fatigue design of welded joints and components[M].IIW Document XIII-1539-96/XV-845-96,1996.

[6]Yousefi F,Witt M,Zenner H.Fatigue strength of welded joints under multiaxial loading:Experiments and calculations[J].Fatigue&Fracture of Engineering Materials&Structures,2001,24(5):339-355.

[7]Jen Y M,Chang L Y,Fang C F.Assessing the fatigue life of butt-welded joints under oblique loading by using local approaches[J].International Journal of Fatigue,2008,30(4):603-613.

[8]Bäckström,Siljander A,Kuitunen R,Ilvonen R.Multiaxial fatigue experiments of square hollow section tube-to-plate welded joints[M].In:Blom AF,edited.Welded high-strength steel structures,EMAS,London,1997:163-177.

[9]Sonsino C M.Multiaxial fatigue of welded joints under in-phase and out-of-phase local strains and stresses[J].International Journal of Fatigue,1995,17(1):55-70.

[10]Sonsino C M,Kueppers M.Multiaxial fatigue of welded joints under constant and variable amplitude loadings[J].Fatigue&Fracture of Engineering Materials&Structures,2001,24(5):309-327.

[11]Siljander A,Kurath P,Lawrence F V.Non-proportional fatigue of welded structures[J].Advances in Fatigue Lifetime Predictive Techniques,ASTM STP,1992,1122:319-338.

[12]Razmjoo G R.Fatigue of load-carrying fillet welded joints under multiaxial loading[J].Fatigue:Core research from TWI,Woodhead,UK,2000:63-99.

[13]Susmel L.Three different ways of using the Modified Wöhler Curve Method to perform the multiaxial fatigue assessment of steel and aluminium welded joints[J].Engineering Failure Analysis,2009,16(4):1074-1089.

[14]刘 刚,黄 一,赵一阳.基于临界面理论的焊接结构多轴疲劳寿命评估方法[J].船舶力学,2013,17(5):494-501.Liu Gang,Huang Yi,Zhao Yiyang.Approach for multiaxial fatigue life assessment of welded structures based on critical plane theory[J].Journal of Ship Mechanics,2013,17(5):494-501.

[15]Archer R.Fatigue of a welded steel attachment under combined direct stress and shear stress[C].Proceedings of the Fatigue of Welded Constructions,1987:63-72.