平板壁面湍流脉动压力及其波数—频率谱的大涡模拟计算分析研究
2014-06-12张晓龙张楠吴宝山中国船舶科学研究中心江苏无锡214082
张晓龙,张楠,吴宝山(中国船舶科学研究中心,江苏无锡214082)
平板壁面湍流脉动压力及其波数—频率谱的大涡模拟计算分析研究
张晓龙,张楠,吴宝山
(中国船舶科学研究中心,江苏无锡214082)
壁面湍流脉动压力是重要的流噪声声源,对壁面湍流脉动压力及其波数—频率谱进行数值计算是流声耦合领域的重要课题,开展相应的研究十分必要。文章采用大涡模拟方法(LES)结合动态亚格子涡模型(DSL)与千万量级的精细网格,对平板壁面湍流脉动压力及其波数—频率谱进行了数值计算,并与试验结果进行了对比分析,验证了数值计算方法的可靠性。首先,介绍了大涡模拟的物理内涵与基本方程,给出了所采用亚格子涡模型的表达式。其次,描述了Abraham试验中矩形试验段的几何特征,给出了网格的剖分形式,并给出了相应的离散求解数值方法以及边界条件的设置。再次,探讨了湍流脉动压力变化规律及其相似律,基于Fourier变换计算得到了湍流脉动压力波数—频率谱,并详细讨论了壁面湍流脉动压力及其波数—频率谱计算值与试验值之间的差异,进行了定量与定性的验证分析,结果表明,计算结果与试验结果吻合良好,计算方法合理可靠,为今后复杂几何模型壁面湍流脉动压力及其波数—频率谱的计算研究工作奠定了基础。最后,基于试验和计算结果,比较分析了常用波数—频率谱理论模型,为波数—频率谱的工程应用提供了参考。
壁面湍流脉动压力;波数—频率谱;大涡模拟;亚格子涡模型
1 引言
由于脉动压力是湍流非定常特性的重要表征,而且是流激噪声的重要来源,所以在流体诱发振动与噪声的许多工程应用问题中脉动压力都备受关注。
湍流脉动压力的研究主要是基于试验测量手段,通过对湍流脉动压力测量数据进行处理和分析,达到对脉动压力定性与定量分析的目的。其研究关注重点是脉动压力的谱型、幅值及变化规律,特别是关注湍流脉动压力波数—频率谱的特性。人们研究湍流脉动压力波数—频率谱的目的主要在于了解湍流结构的时空关联特性以及为流激结构振动声辐射提供输入。
自上世纪中叶Corcos[1-2]基于Fourier变换得到最早的波数—频率谱模型以来,湍流脉动压力主要分析手段一直都是基于Fourier变换,在频域和波数域内,对脉动压力的时空关联特性、多尺度特性等进行分析研究。具体说来就是将试验得到脉动压力数据进行时、空傅里叶变换,最终得到脉动压力的波数—频率谱和功率谱并进行研究。毋庸置疑,基于Fourier变换的频谱分析在湍流脉动压力的研究中发挥了巨大作用,Fourier变换物理概念清晰,简便易行,数据直观,便于理解,加深了我们对湍流脉动压力以及湍流现象的深入理解,现在仍是研究湍流脉动压力的主要分析手段。
简言之,目前对于湍流脉动压力,尤其是其波数—频率谱的大量研究主要是以试验测量和Fourier分析为主要手段。
Abraham和Keith(1998)[3]在消音水洞中,通过在流向等间距布置48个传感器,测得了壁面湍流脉动压力流向的波数—频率谱,其使用的传感器阵列具有较高的分辨率,从而保证了波数—频率谱“迁移脊”和部分低波数区域的测量准确度。用基于试验测得的参数得到的时空尺度对波数—频率谱进行了归一化处理,比较了不同归一化处理方式的效果。
Cipolla和Keith(2008)[4]在庞多雷湖(Lake Pend Oreille)中进行圆柱表面拖曳阵上的湍流脉动压力测试,试验在实尺度模型上进行,速度范围为10-18节,并得到了相应的波数—频率谱、自功率谱和迁移速度等。试验结果表明当直拖时,波数—频率谱中有明显的迁移脊;当回转时,流体诱发的振动会主要影响波数—频率谱的低频部分,高频部分则更快地衰减。在分析测试数据时Cipolla和Keith仍然引用Abraham(1998)的试验结果来证实其测试结果的合理性,这也足见Abraham(1998)的测量结果已得到业界认可,具有经典价值,对湍流脉动压力测量与波数—频率谱的分析均产生了重要影响。
Bonness(2010)等人[5]基于湍流脉动压力激发的圆柱管道振动数据,对低波数区域充分发展的管道湍流边界层脉动压力进行了测量,并基于试验测量结果对几种常用波数—频率谱模型进行了比较分析。结果表明,Corcos模型预报结果偏大,波数—频率谱测量值介于Smol'yakov模型和Chase模型之间。
当前,随着数值模拟方法的逐渐成熟和计算水平的提高,人们也开始对湍流脉动压力进行数值模拟计算研究。
Manoha(2000)等人[6]采用大涡模拟方法,对厚平板钝后缘的非稳态流场的脉动压力进行了计算,并对尾缘壁面脉动压力进行了分析,其幅值、频率以及流向的演化均与钝后缘翼型的测量结果吻合很好。
Wang Meng(2009)等[7-9]应用LES方法对有拱度薄板机翼低速情况下的脉动压力进行计算,并结合FW-H方程对辐射噪声进行了计算。计算得到机翼表面导边区域压力场的频谱和展向相关性均与试验吻合较好,但低频域附近较差。远场声压谱与试验结果很吻合,其引入的有限弦长修正虽然比较小,但能进一步提高准确度。
Jean-François和Klaus(2009)[10]用DES对后台阶流动的脉动压力进行了计算,计算得到的脉动压力主频率与试验吻合很好,功率谱与经验模型一致。
张楠(2008-2011)等人[11-15]通过LES结合FW-H声学类比方法,计算了两类孔穴的流激噪声问题以及五种不同尺寸的方形孔腔在水中的流动特征及流激噪声。还基于LES和Kirchhoff积分,对孔腔流动的发声机理进行了分析。另外,利用大涡模拟计算了SUBOFF主、附体的表面压力分布,并对平板及水下航行体几个离散点的脉动压力进行了计算,计算结果与试验结果十分吻合,具有较高精度;平板脉动压力与试验值差异小于5 dB,比较可靠。
从湍流脉动压力及其波数—频率谱的国内外研究进展可以看出,其数值计算研究主要还是局限于单点脉动压力的计算与验证研究,尚未发现国际上有关湍流脉动压力波数—频率谱CFD详细计算验证研究的公开文献。因此,本文将基于大涡模拟方法对平板壁面湍流脉动压力及变化规律、湍流脉动压力相似律,尤其是其波数—频率谱展开数值计算与验证分析研究。
2 计算方法
2.1 大涡模拟方法
大涡模拟(LES)的主要思想是:将湍流分解为可解尺度湍流运动(包含大尺度脉动)和不可解尺度湍流运动(包含所有小尺度脉动),并且认为,大尺度运动几乎包含所有的能量,而小尺度运动主要起能量耗散作用,几乎不受流场边界形状或平均运动的影响,近似认为是各向同性的。然后,小尺度运动对大尺度运动的作用通过建立模型(即亚格子涡模型)来实现,从而使运动方程封闭。对可解尺度运动则直接进行数值求解。
物理空间的滤波过程可表示如下:

滤波后的控制方程(连续方程和N-S方程)为:

其中:σij为分子粘性引起的应力张量,τij为亚格子应力张量,需要用亚格子涡模型进行模拟。本文采用DSL亚格子涡模型进行计算,该模型由Germano(1991)[16]提出,后来,Lilly(1992)[17]应用最小二乘法又对其作了改进。它通过局部计算涡粘性系数来尽可能地反映实际流动情况,通过对最小可解尺度的信息进行采样,然后利用这些信息来模拟亚格子尺度应力。此模型在接近壁面边界时给出了正确的渐近特性,因此也就不需要阻尼函数或者间歇函数,而且此模型还能够考虑逆散射的影响。

其中:其中Lij为可解的湍流应力,它表征介于网格滤波宽度与测试滤波宽度之间的雷诺应力的贡献。Mij是一个与滤波宽度和应变率张量有关的中间量。
2.2 湍流脉动压力波数—频率谱及其计算分析方法
目前湍流脉动压力的分析主要还是采用傅里叶分析来实现时间—空间和波数—频率域之间的转换,进而能够在波数—频率域内研究湍流脉动信号的统计特性。湍流脉动压力波数—频率谱定义为湍流脉动压力时—空信号的相关函数在时间和空间内的傅里叶变换,数学表达式为:

在实际中,通常通过对湍流脉动压力离散时空信号进行快速傅里叶变换(FFT),然后对其幅值的平方进行系综平均得到湍流脉动压力的波数—频率谱[3]。此时,湍流脉动压力波数—频率谱表达式如下:
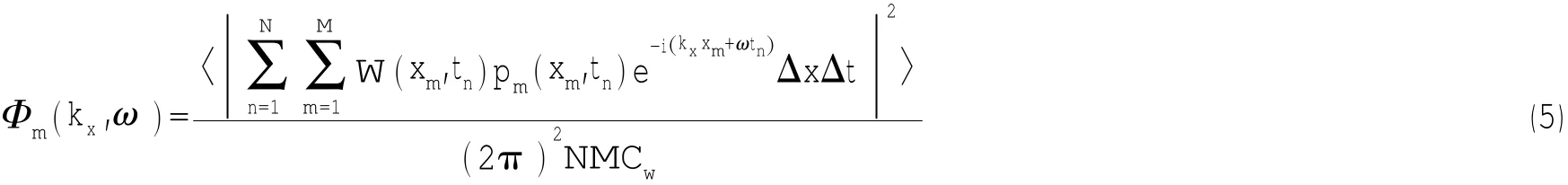
其中:符号〈〉代表期望值,pm表示第m个传感器测得的脉动压力,N为时间结点数,M为传感器个数,Δx为传感器间距,Δt为时间步长,

则为窗常数。
2.3 计算模型、网格及数值方法
众所周知,Huang在风洞中所做的SUBOFF潜艇尾流场测试已经成为水动力学界公认的标模基准检验试验(Benchmark test),国际与国内的水动力学研究人员都用此试验数据来校核数值计算方法的可靠性。同样,Abraham在安静性水筒中所做的平板湍流脉动压力测试也已经成为声学领域的标模基准检验试验,可以用来校核对声源的CFD计算方法的可靠性。二者在各自领域都产生了重要而深远的影响。本文即利用Abraham的试验数据详细验证了大涡模拟方法对于非定常流动和脉动压力的计算能力。
如图1所示,Abraham试验的矩形试验段长L=2.108 2 m,入口处矩形剖面宽a=0.304 8 m,高h= 0.101 6m;出口处矩形剖面宽a1=0.304 8m,高h1=0.112 0m。从距入口端1.63m处开始,流向等间距布置48个传感器,传感器直径3.81mm,传感器中心间距4.22mm。Abraham试验的三个工况入口处水流速度分别为U0=3.1m/s,4.6m/s和6.1m/s,测试点处的局部雷诺数分别约为Re=4.47×106,6.70× 106和1.02×107。依照流体力学理论,平板边界层在Rex>3.0×106之后就已发展为湍流状态。
本文采用三维模型计算,计算域采用结构化网格,网格剖分形式采用H型,网格数量为1 250万,计算区域网格如图2所示。其涡粘性系数由下式给出:

图1 槽道试验段及传感器布置示意图Fig.1 The rectangular test section and sensor array
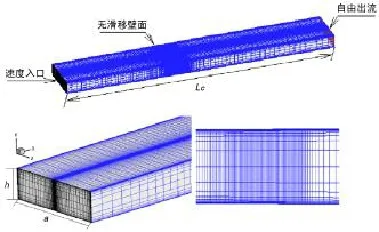
图2 计算区域网格Fig.2 The computational domain and grid
计算区域长Lc=2L,入口处矩形剖面宽a=0.304 8m,高h=0.101 6m;出口处矩形剖面宽a1=0.304 8 m,高h1=0.112 0m;边界条件设为速度入口、自由出流以及无滑移壁面边界条件;时间项采用二阶隐式格式离散,动量方程采用限界中心差分格式离散,压力速度耦合采用SIMPLE算法;计算时间步长Δt=10-4s,壁面y+≈1。
3 计算结果与分析
3.1 脉动压力计算结果验证与分析
图3给出了不同速度下湍流脉动压力计算结果与试验结果的对比。本文给出的湍流脉动压力频谱计算结果均为归一化三分之一倍频程(1/3OCT)频谱,横轴为纵轴为10loω为圆频率,δ*为边界层排挤厚度,U0为来流速度,Φ(ω)为自功率谱幅值。
从图3可以看出:定性来看,计算得到的脉动压力自功率谱均表现出湍流脉动压力自功率谱的典型特性:频谱在低频区域呈现“平台区”,在高频区域随频率的增加以一定的斜率衰减,且频谱均在归一化频率ωδ*/U0=2附近开始衰减,这与Abraham的试验结果一致;定量来看,当U0=6.1m/s、4.6m/s和3.1m/s时,低频段(ωδ*/U0<2)计算误差分别为4.1 dB、-3.4 dB和-5.0 dB(负号表示小于试验值),高频段计算误差分别为-4.0 dB、-5.9 dB和5.1 dB。即低频段计算误差小于5 dB,高频段计算误差小于6 dB,计算精度与国际上已有的研究一致[7-9]。

图3 脉动压力频谱计算结果与试验结果对比:(a)U0=6.1m/s;(b)U0=4.6m/s;(c)U0=3.1m/sFig.3 Comparison of the frequency spectra of computation and experiments: (a)U0=6.1m/s;(b)U0=4.6m/s;(c)U0=3.1m/s
3.2 脉动压力变化规律及相似律探讨
以下对平板湍流脉动压力的系列计算结果展开进一步的讨论。
图4给出了四个不同监测点以声压谱级表达的自功率谱随速度的变化(图中字母Plate表示平板,下同)。自功率谱的平台区(ωδ*/U0<2)谱级平均值详细数据如表1所示。从表中可以看出,当U0= 6.1m/s、4.6m/s和3.1m/s时,自功率谱平台区谱级的四测点平均值分别为131 dB、123.3 dB和116 dB。在所计算的频段范围内,自功率谱谱级随速度的减小而减小:与U0=6.1m/s相比,U0=4.6m/s和3.1m/s时谱级在低频区域(ωδ*/U0<2)平均减小值分别为-7.7 dB和-15 dB(负号表示减小);在高频区域(ωδ*/U0>2)平均减小值分别为-20 dB和-32 dB。四个测点衰减频率一致,当U0=6.1m/s、4.6m/s和3.1m/s时,衰减频率分别为513 Hz、374 Hz和197 Hz,即均在ωδ*/U0=2附近开始衰减。

由以上的定量分析可知,平板湍流脉动压力的自功率谱受速度的影响十分明显。随着速度的减小,自功率谱谱级降低;同时自功率谱在更低的频率提前衰减,即平台区处于更低的频段范围,也就是说主要能量集中于频率更低的区域,且能级相对较低。这与Abraham试验结果中关于波数—频率谱能量分布随速度的变化规律也是吻合的,有关波数—频率谱讨论见下文。
图5~10给出了不同速度下所有监测点的自功率谱,以便于湍流脉动压力相似律的探讨。
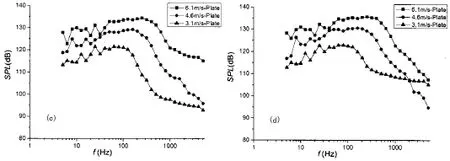
图4 不同测点处自功率谱随速度的变化:(a)测点1;(b)测点16;(c)测点32;(d)测点48Fig.4 Frequency spectra of differentmonitors at different velocities:(a)monitor-1;(b)monitor-16; (c)monitor-32;(d)monitor-48
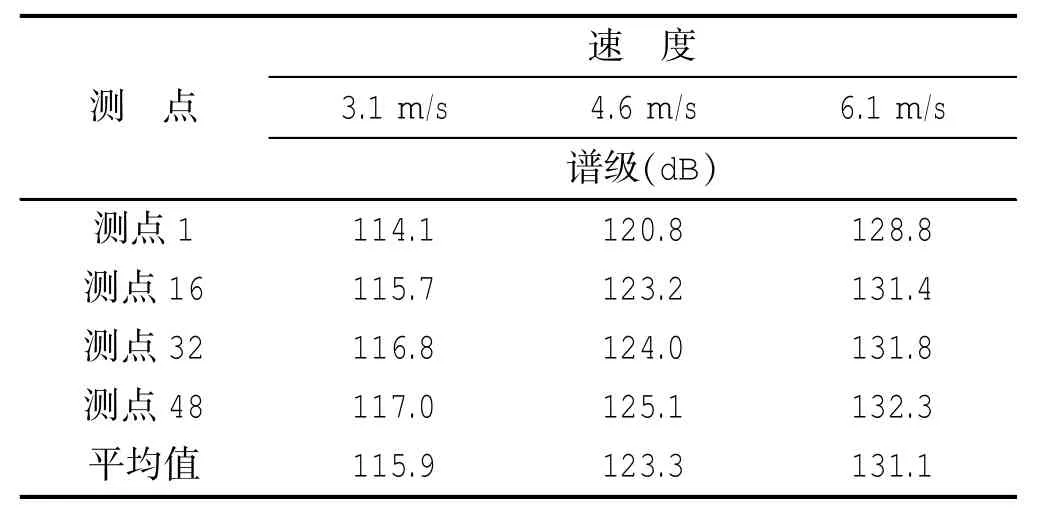
表1 不同监测点不同速度下的自功率谱平台区谱级(单位:dB)Tab.1 Spectral level of differentmonitors
湍流的相似律理论认为,壁面湍流脉动压力频谱的不同区域来自于湍流边界层不同位置处、不同尺度湍流运动的贡献,频谱的低频区域与外层湍流边界层的大尺度量直接相关,高频区域则与底层的小尺度量直接相关。Keith(1992)[18]认为在探讨壁面湍流脉动压力相似律时可采用三种方式对频谱进行归一化处理:

由于湍流边界层本身的相似性,选取代表大尺度量或小尺度量的归一化尺度(外部变量或内部变量)对频谱进行归一化处理,可以使频谱不同尺度、不同流速下的对应区域汇聚。由于低频代表大尺度运动,用外部变量进行归一化处理,使得低频汇聚,高频散开;同理,用内部变量进行归一化处理,则会使得高频汇聚,低频散开。由于湍流相似律与频谱的普适性直接相关,进而直接影响脉动压力频谱的实际应用,其研究与探讨也是当今热点。
图5~10所给出的不同速度下所有监测点的自功率谱均采用外部变量ρ、U0和进行归一化处理,这与Abraham试验结果的处理方式也保持一致。
从图5~10所给出的处理结果可以看出,计算得到的湍流脉动压力频谱采用外部变量ρ、U0和δ*进行归一化处理之后,在低频段范围内(),归一化的湍流脉动压力频谱谱级均汇聚于小于5 dB的小范围内;而在高频段范围内),频谱谱级之间的差别最大可达30 dB。也就是说,计算得到的归一化的频谱在低频汇聚,高频发散。这充分说明平板湍流脉动压力频谱的低频区域主要来自于外层湍流边界层大尺度运动的贡献,且与湍流脉动压力的相似理论及国际上已有的研究吻合[19-25],充分体现了湍流脉动压力相似律。同时,计算结果对于湍流脉动压力相似律的体现也充分说明本文计算方法可靠,计算结果合理。
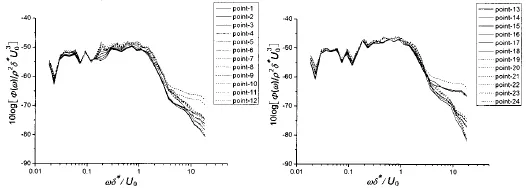
图5 平板不同监测点处脉动压力的自功率谱(U0=6.1m/s,测点1-24)Fig.5 Frequency spectra of differentmonitors(U0=6.1m/s,monitor 1-24)

图6 平板不同监测点处脉动压力的自功率谱(U0=6.1m/s,测点25-48)Fig.6 Frequency spectra of differentmonitors(U0=6.1m/s,monitor 25-48)

图7 平板不同监测点处脉动压力的自功率谱(U0=4.6m/s,测点1-24)Fig.7 Frequency spectra of differentmonitors(U0=4.6m/s,monitor 1-24)

图8 平板不同监测点处脉动压力的自功率谱(U0=4.6m/s,测点25-48)Fig.8 Frequency spectra of differentmonitors(U0=4.6m/s,monitor 25-48)

图9 平板不同监测点处脉动压力的自功率谱(U0=3.1m/s,测点1-24)Fig.9 Frequency spectra of differentmonitors(U0=3.1m/s,monitor 1-24)

图10 平板不同监测点处脉动压力的自功率谱(U0=3.1m/s,测点25-48)Fig.10 Frequency spectra of differentmonitors(U0=3.1m/s,monitor 25-48)

3.3 波数—频率谱计算结果验证与分析
图11给出了三个速度下计算得到的波数—频率谱三维视图,借以对波数—频率谱的物理意义加以说明。如图11所示,谱级最高的部分称为湍流脉动压力波数—频率谱的“迁移脊”。迁移脊代表了湍流的大部分能量(含能涡)的主要分布区域。而迁移脊的斜率dω/d k=Uc定义为迁移速度,表示湍流中的涡旋结构(拟序结构)的平均迁移速度,它与湍流中涡旋结构(拟序结构)以及能量的迁移和传递息息相关。对湍流脉动压力的波数—频率谱进行研究,可以深入揭示湍流能量的分布规律以及外界条件的改变对湍流能量分布规律的影响,进而指导湍流流动相关的实际工程应用。
图12~14给出了平板波数-频率谱的计算结果与Abraham的试验结果,表2给出了平板波数-频率谱主要参数计算与试验结果的详细对比数据。首先,从图12~14及表2的数据可以看出,含能涡主要分布区域,即迁移脊在频率—波数域内的分布范围与试验一致,迁移脊宽度也与试验结果相当。且随频率增加,迁移脊变宽,幅值降低,这与Abraham试验结果以及波数-频率谱理论模型是吻合的[26-31]。谱级最高的部分,即能量最高的含能涡,也就是大尺度涡,均分布在小于200 Hz的低频范围内,说明大尺度涡对应频谱的低频区域,这与国际上已有的研究一致[32-33]。
其次,就波数—频率谱谱级而言,计算得到的不同来流速度下平板湍流脉动压力波数—频率谱谱级峰值与试验吻合较好,当U0=6.1 m/s、4.6 m/s和3.1m/s时相应的谱级峰值分别为-25.1 dB、-30.2 dB和-36.2 dB(谱级为负值是由于具体处理方法造成的,并不影响分析,这种处理方法在声学研究中很常见),与试验相比,计算误差分别为-5.1 dB、-5.2 dB和-6.2 dB(负号表示小于试验值),即波数—频率谱谱级峰值计算误差均小于7 dB。随来流速度减小,波数-频率谱谱级降低,这与Abraham的试验一致,同时波数—频率谱谱级随速度的定性变化规律与自功率谱随速度的变化规律一致。
再次,就涡旋结构的迁移速度而言,在U0=6.1m/s、4.6m/s和3.1m/s时,计算得到的迁移速度Uc= dω/d k分别为4.24 m/s、3.18 m/s和2.28 m/s,相应的无量纲化迁移速度Uc/U0分别为0.71、0.69和0.69,与试验相比误差分别为4.5%,3.0%和12.7%,计算误差均在合理范围内。
最后,对以上数据进一步分析可知,与U0=6.1m/s和U0=4.6m/s相比,当U0=3.1m/s时,波数—频率谱主要参数(包括:谱级、含能涡分布范围以及迁移速度等)计算误差均稍大,主要原因在于:来流速度较低时,流动必然包含转捩的影响,而亚格子涡模型均为湍流模型,是基于完全发展湍流出发而建立的,其基于完全发展湍流对涡粘性进行模拟时会引起计算误差。
综合以上分析可以看出,计算得到的平板湍流脉动压力波数—频率谱主要参数(包括:谱级、迁移速度、含能涡分布范围以及能量在频率—波数域内的分布规律等)均与试验结果吻合很好,说明论文的计算结果合理可靠。

图11 计算得到的平板湍流脉动压力波数—频率谱三维视图:(a)U0=6.1m/s;(b)U0=4.6m/s;(c)U0=3.1m/sFig.11 Three dimensional plotof the computed wavenumber-frequency spectra: (a)U0=6.1m/s;(b)U0=4.6m/s;(c)U0=3.1m/s

图12 平板频率—波数谱计算结果与试验的对比(U0=6.1m/s):(a)计算结果;(b)试验结果Fig.12 Comparison of the computed and experimentalwavenumber-frequency spectra(U0=6.1m/s): (a)computation;(b)experiment
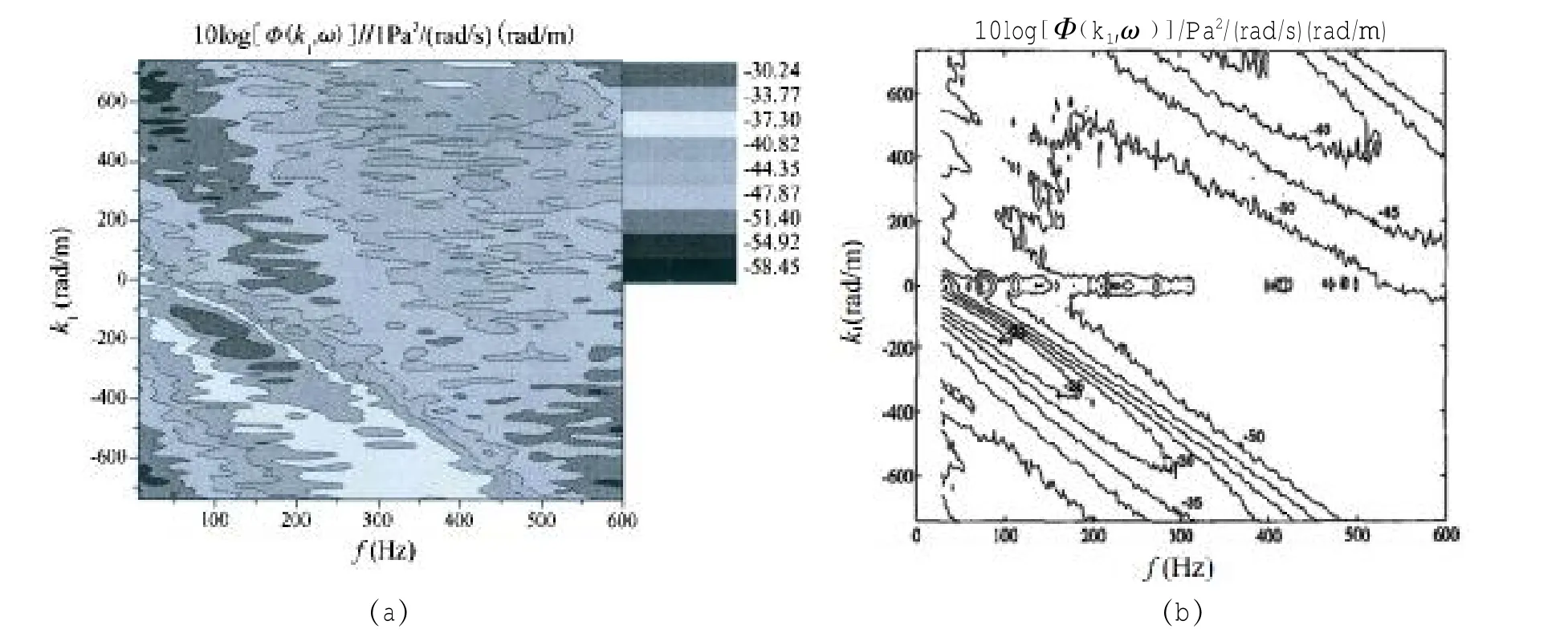
图13 平板频率—波数谱计算结果与试验的对比(U0=4.6m/s):(a)计算结果;(b)试验结果Fig.13 Comparison of the computed and experimentalwavenumber-frequency spectra(U0=4.6m/s): (a)computation;(b)experiment

图14 平板频率—波数谱计算结果与试验的对比(U0=3.1m/s):(a)计算结果;(b)试验结果Fig.14 Comparison of the computed and experimentalwavenumber-frequency spectra(U0=3.1m/s): (a)computation;(b)experiment

表2 平板频率—波数谱计算结果与试验的比较Tab.2 Comparison of the computed and experimentalwavenumber-frequency spectra
3.4 波数—频率谱计算结果与不同理论模型的对比分析
图15给出了数值计算、试验以及理论模型所得的波数—频率谱(此处取波数—频率谱在频率f=100 Hz处的剖面结果),以便于对湍流脉动压力波数—频率谱及其常用理论模型展开进一步分析。其中,Convoluted Chase Model表示考虑传感器尺寸的影响,将Chase模型与传感器响应函数卷积之后的结果。
就计算结果而言,迁移脊峰值所在波数(迁移波数)为-135.1 rad/m,这与Abraham试验结果和理论模型十分一致,迁移脊峰值谱级与Abraham试验结果相比误差为-3.1 dB(负号表示小于Abraham试验值,下同),在所计算的波数域范围内谱级最大计算误差为-6.7 dB。可见,计算结果与Abraham试验结果吻合很好。
就波数—频率谱理论模型而言,在迁移波数附近的波数域范围内,不同的理论模型与试验值和计算结果均较为吻合,相互之间差别小于6.9 dB。
由此可见,在低波数范围内,Corcos模型误差偏大,Chase模型和卷积后的Chase模型(Convoluted Chase Model)均与试验和数值计算结果吻合,卷积后的Chase模型效果更好。

图15 波数—频率谱数值计算结果与Abraham试验结果及常用理论模型的对比(U0=6.1m/s,f=100 Hz)Fig.15 Comparison of the wavenumber-frequency spectramodelwith computational and experimental data(U0=6.1m/s,f=100 Hz)
4 结论与展望
本文用大涡模拟方法,结合动态DSL亚格子涡模型及千万量级精细网格平板壁面湍流脉动压力及其波数—频率谱进行了计算,并基于Abraham经典试验对计算结果进行了验证与深入分析,基于本文的工作,得到的主要结论如下:
(1)在论文计算的频段内,湍流脉动压力自功率谱计算误差小于6 dB,计算精度与国际上研究一致。
(2)计算得到的波数—频率谱主要参数包括:迁移脊量级、宽度、波数—频率域分布范围及迁移速度等均与Abraham试验结果吻合很好,说明论文计算结果可信,论文建立的数值计算方法合理可靠。
(3)湍流脉动压力的自功率谱及波数—频率谱与来流速度直接相关,谱级随速度的增加而增大。
(4)从计算和试验结果来看,在迁移波数附近的波数域范围内,不同的理论模型均与试验值和计算结果均较为吻合;而在低波数区域,Corcos模型预报值明显偏高,Chase模型与试验值和计算结果吻合较好。
综上所述,本文所建立的数值计算方法切实可靠,可以用于壁面湍流脉动压力及其波数—频率谱的计算与分析研究,为复杂形状的壁面湍流脉动压力及其波数—频率谱进一步的研究工作打下了基础。
[1]Corcos GM.The structure of the turbulent pressure field in boundary layer flows[J].Journal of FIuid Mechanics,1964,18 (3):353-378.
[2]Corcos GM.The resolution of turbulent pressure at the wall of a boundary layer[J].Journal Sound and Vibration,1967,6 (1):59-70.
[3]Abraham BM,Keith W L.Directmeasurements of turbulent boundary layerwall pressure wavenumber-frequency spectra [J].Journal of Fluids Engineering,1998,120(3):29-39.
[4]Cipolla K M,Keith W L.Measurements of the wall pressure spectra on a full-scale experimental towed array[J].Ocean Engineering,2008,35(3):1052-1059.
[5]BonnessW K,Capone D E,Hambric SA.Low wavenumber turbulent boundary layerwall pressuremeasurments from vibration data on a cylinder in pipe flow[J].Journal of Sound and Vibration,2010,329:4166-4180.
[6]Manoha E,Troff B,Sagaut P.Trailing-edge noise prediction using large-eddy simulation and acoustic analogy[J].AIAA Journal,2000,38(4):575-583.
[7]Wang Meng.Computation of trailing-edge flow and noise at low Mach number using LESand acoustic analogy[J].Annual Research Briefs,Center for Turbulence Research,Stanford University,1998.
[8]Wang Meng,Moin P.Computation of trailing-edge flow and noise using large-eddy simulation[J].AIAA Journal,2000,38 (12):2201-2209.
[9]Wang Meng,Moreau S,Iaccarinoand G,Roger M.LES prediction ofwall-pressure fluctuations and noise of a low-speed airfoil[J].International Journal of Aeroacoustics,2009,8(3):177-198.
[10]Dietiker Jean-François,Hoffmann K A.Predicting wall pressure fluctuation over a backward-facing step using detached eddy simulation[J].Journal of Aircraft,2009,46(6):2115-2020.
[11]张楠,沈泓萃,姚惠之,朱锡清,俞孟萨.孔穴流激噪声的计算与验证研究[J].船舶力学,2008,12(5):799-805. Zhang Nan,Shen Hongcui,et al.Validation and calculation of flow induced noise of cavity[J]Journal of Ship Mechanics, 2008,12(5):799-805.
[12]张楠,沈泓萃,姚惠之,田于逵,谢华.水下航行体壁面脉动压力的大涡模拟研究[J].水动力学研究与进展, 2010,25(1):106-112.
[13]张楠,沈泓萃,朱锡清,姚惠之,谢华.三维孔腔流激噪声的大涡模拟与声学类比预报与验证研究[J].船舶力学, 2010,14(1-2):181-190. Zhang Nan,Shen Hongcui,et al.Validation and prediction of flow induced noise of 3-dimensional cavity with large eddy simulation and acoustic analogy[J].Journal of Ship Mechanics,2010,14(1-2):181-190.
[14]张楠,沈泓萃,朱锡清,姚惠之.基于大涡模拟和Kirchhoff积分方法的孔腔流动发声机理分析[J].船舶力学,2011, 15(4):427-434. Zhang Nan,Shen Hongcui,et al.Analysis of themechanism of cavity flow induced noise with large eddy simulation and Kirchhoffmethod integral[J].Journal of Ship Mechanics,2011,15(4):427-434.
[15]张楠.孔腔流动和流激噪声机理及耦合计算方法研究[D].无锡:中国船舶科学研究中心,2010.
[16]Germano M,Piomelli U,CabotW H.A dynamic subgrid-scale eddy viscositymodel[J].Phys.Fluids 1991,A3(7):1760-1765.
[17]Lilly D K.A proposedmodification of the germano subgrid scale closuremethod[J].Phys.Fluids 1992,A4(3):633-635.
[18]Keith W L,Hurdis D A,Abraham B M.A comparison of turbulent boundary layer wall pressure spectrum[J].Journal of Fluids Engineering,1992,114:338-347.
[19]Willmarth W W.Pressure fluctuations beneath turbulent boundary layers[J].Anual Review of Fluid Mechanics,1975,7: 13-36.
[20]Keith W L,Bennet JC.Low frequency spectra of the wall shear stress and wall pressure in a turbulentboundary layer[J]. AIAA Journal,1990,29(4):526-530.
[21]Arguillat B,Ricot D,et al.Measured wavenumber frequency spectrum associated with acoustic and aerodynamic wall pressure fluctuations[J].Journal of the Acoustical Society of America,2010,128(4):1647-1655.
[22]Blake W K,Chase D M.Wavenumber frequency spectra of turbulent boundary layer pressuremeasured by microphone arrays[J].Journal of the Acoustical Society of America,1971,49(3):862-877.
[23]Blake W K.Turbulent boundary layer wall pressure fluctuations on smooth and rough walls[J].Journal of Fluid Mechanics,1970,44(4):637-660.
[24]Haecheon Choi,Parviz Moin.On the space-time charateristics ofwall pressure fluctuations[J].Phys.Fluids,1990,A2(8): 1450-1460.
[25]Craig N D,Michael R H,Charles E T.A laboratory scale piezoelectric array for underwatermeasurements of the wall pressure spectra beneath turbulentbounday layers[J].Meas.Sci.Technol,2012,23:1-11.
[26]Corcos G M.The structure of the turbulent pressure field in boundary layer flows[J].Journal of FIuid Mechanics,1964, 18(3):353-378.
[27]Smol'yakav A V,Tkachenko V M.Themeasurementof turbulent fluctuation[M].Translated by Chomet S.,Springer-Verlag,1983.
[28]Chase D M.Modeling theWavevector-frequency spectrum of turbulent boundary layer wall pressure[J].Journal of Sound and Vibration,1980,70:29-67.
[29]Abraham BM,Keith W L.Directmeasurements of turbulent boundary layerwall pressure wavenumber-frequency spectra [J].Journal of Fluids Engineering,1998,120(3):29-39.
[30]Wills JA B.Measurements of the wavenumber/phase velocity spectrum ofwall pressure beneath a turbulent boundary layer [J].Journal of Fluid Mechanics,1970,45(1):65-90.
[31]Panton R L,Robert G.The Wavenumber-phase velocity representation for the turbulentwall pressure spectrum[J].Journal of Fluids Engineering,1994,116:477-483.
[32]Haecheon Choi,Parviz Moin.On the space-time charateristics ofwall pressure fluctuations[J].Phys.Fluids,1990,A2(8): 1450-1460.
[33]Farabee TM,Casarella M J.Spectral features of wall pressure fluctuations beneath turbulent boundary layers[J].Phys. Fluids,1991,A3(10):2410-2420.
Com putation of turbulent wall pressure fluctuation and itswavenumber-frequency spectrum using large eddy simulation
ZHANG Xiao-long,ZHANG Nan,WU Bao-shan
(China Ship Scientific Research Center,Wuxi214082,China)
Turbulentwall pressure fluctuations beneath turbulent boundary layers are important sources of flow noise.The computation ofwall pressure fluctuation and itswavenumber-frequency spectrum is a hot topic in the field of flow-acoustic coupling.It is necessary to carry out corresponding research.In this paper,wall pressure fluctuation and itswavenumber-frequency spectrum are computed using large eddy simulation(LES)with approriate sub-grid scalemodel,grid number and discretization methods.The results are compared with the experiment of Abraham and discussed in detail.Firstly,some fundamentals of the numerical simulation are presented,including the philosophy of LES,formulations of sub-grid scalemodels, discretization methods and boundary conditions,etc.Secondly,the rectangular test section of Abraham's experiment and its computational domain are depicted.Thirdly,the scaling of turbulentwall pressure fluctuations and its variations due to different free stream velocities are discussed.The wavenumber-frequencyspectra of turbulent wall pressure fluctuations are computed by taking FFT of the correlation function of the simulation data,the computed spectra of the wall pressure fluctuations are compared with those of Abraham's experiment and analyzed qualitatively and quantitatively.Finally,comparison of typical theoretical models of wavenumber-frequency spectra ismade based on computational and Abraham's experimental results.Groundwork ismade for further research in turbulentwall pressure fluctuation and itswavenumberfrequency spectrum.
turbulentwall pressure fluctuations;wavenumber-frequency spectrum;LES
O357.5
A
10.3969/j.issn.1007-7294.2014.10.001
1007-7294(2014)10-1151-14
2014-06-15
国家自然科学基金(51079133);江苏省自然科学基金(BK2010162)
张晓龙(1988-),男,中国船舶科学研究中心硕士研究生,E-mail:ChalonJon@outlook.com;张楠(1977-),男,博士,中国船舶科学研究中心高级工程师。
