定位坐标分量依赖于卫星高度角的灵敏度分析
2014-12-12岳俊,何冰
岳 俊,何 冰
(1.北京大学地球与空间科学学院,北京100871;2.武汉大学测绘学院,湖北武汉430079)
一、引 言
在GPS外业测量中,经常会遇到遮挡导致高度角变大的情况,影响测量精度,要减小高度角通常要付出一定成本。本文通过大量统计分析出对测量精度影响最大的截止高度角,测量时使遮挡产生的高度角小于此截止高度角通常会得到较大的效益。本文的结果将为GPS外业观测计划的制订提供参考。
DOP值通常到了一定高度角就会产生显著变化,但仅通过DOP值的数值变化并不能正常反映其依赖于卫星截止高度角的灵敏度。本文提出了GPS不可用率并用其衡量DOP值的变化,对GPS不可用率进行小波滤噪和曲线拟合,求出其对应的分布函数和概率密度函数,以此计算各个DOP值的灵敏度。同时本文通过大量的数据处理,建立了5种DOP值之间的统计经验模型。
二、DOP值依赖于卫星截止高度角的变化规律
获得高精度定位结果的重要因素是可视卫星拥有良好的几何图形结构,尤其是对单点定位和定态测量而言。可见性是指卫星和接收机之间的通视。由于卫星和用户间存在相对运动,卫星的空间几何图形结构会随时间而变化。瞬时卫星几何图形一般采用精度衰减因子(dilution of precision,DOP)进行评定[1]。
由于DOP值的计算依赖于卫星高度角,当截止卫星高度角变化时,可见卫星数和DOP值随之发生变化,DOP值在单历元依赖于卫星高度角的变化情况如图1所示。
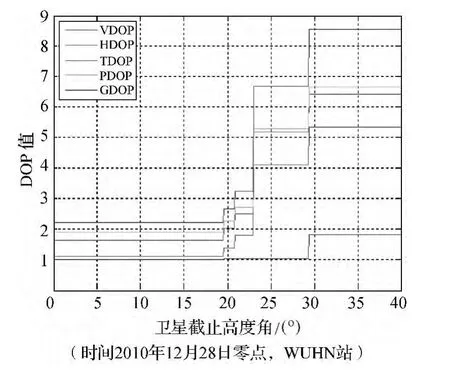
图1 单历元DOP值随卫星截止高度角的变化
由图1及DOP值计算方法可知,只有截止高度角处存在,卫星DOP才会发生变化,因此对于单历元,截止高度角-DOP值二维图为阶越型。为了得到DOP值随着高度角变化的统计规律,对单天96个历元的DOP值按角度取平均,得到图2。
由图2可以分析出,由于DOP值的计算方法,DOP值会随着卫星截止高度角的增大而显著增大,如果直接对DOP值进行拟合,将难以得出符合实际的定位坐标分量精度依赖于卫星高度角的灵敏度,因此本文拟从统计学的角度得出卫星高度角的灵敏度。对此,本文提出“GPS不可用率”这个概念。

图2 96历元平均DOP值随卫星截止高度角的变化
GPS卫星可用性是指GPS系统的服务可以使用的时间的百分比,由文献[2]分析得知,GPS可用性将取决于精度要求的严格程度,其分析认为PDOP≤6为GPS可用性的门限。由此可得,对于单历元必有唯一一个门限高度角。对于多个历元,每一个高度角均对应一个GPS可用历元数,将GPS可用历元数除以总历元数定义为GPS可用率,将历元数减GPS可用历元数除以总历元数定义为GPS不可用率。
GPS不可用率随着卫星高度角的增加而增大,最小值为0,最大值为1。GPS不可用率越高,表明定位精度越低。从中可以找到GPS卫星可用率随着卫星截止高度角变化的灵敏度,并计算灵敏度最大值,在全球范围内得出灵敏度的置信区间。
由于文献[2]仅给出了 GPS可用性选择的PDOP门限值,对10周数据进行建模,构建VDOP、HDOP、TDOP、GDOP与 PDOP的经验关系,以此求出 GPS 可用性选择的 VDOP、HDOP、TDOP、GDOP门限值。
取截止高度角为40°,对10周共70天6720个历元的数据进行DOP值数据拟合。数据拟合如图3所示。
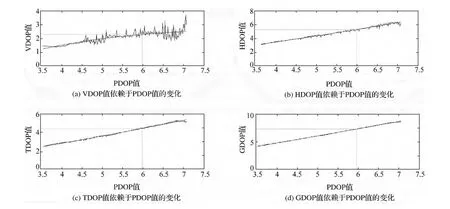
图3 DOP值数据拟合
由DOP值拟合曲线方程可以得知,PDOP值为6 时,HDOP、VDOP、TDOP、GDOP 分别为 2.394 5、5.492 7、4.601 1、7.561 4,满足 DOP 值的基本关系方程。将这些值分别取为门限DOP值,由5个门限DOP值对应的门限高度角所计算出来的GPS不可用率随卫星的变化如图4所示。
由图4可得,通过取5种DOP值的门限值计算出来的GPS不可用率几乎相同,证明GPS不可用率的概念有其重要的价值,在单个DOP值计算中,如果截止高度角内的卫星数小于4则无法计算出来,通过计算GPS不可用率这个统计值可以得到GPS定位精度随着高度角的变化值。
三、基于小波滤波和曲线拟合的灵敏度计算
在得到DOP值概率分布离散形式后,由于数据处理过程的不完善等因素,必然会存在高频的噪声,因此需要对采集到的离散的概率分布函数进行滤波降噪。本文中采用小波变换的方式进行去噪处理。
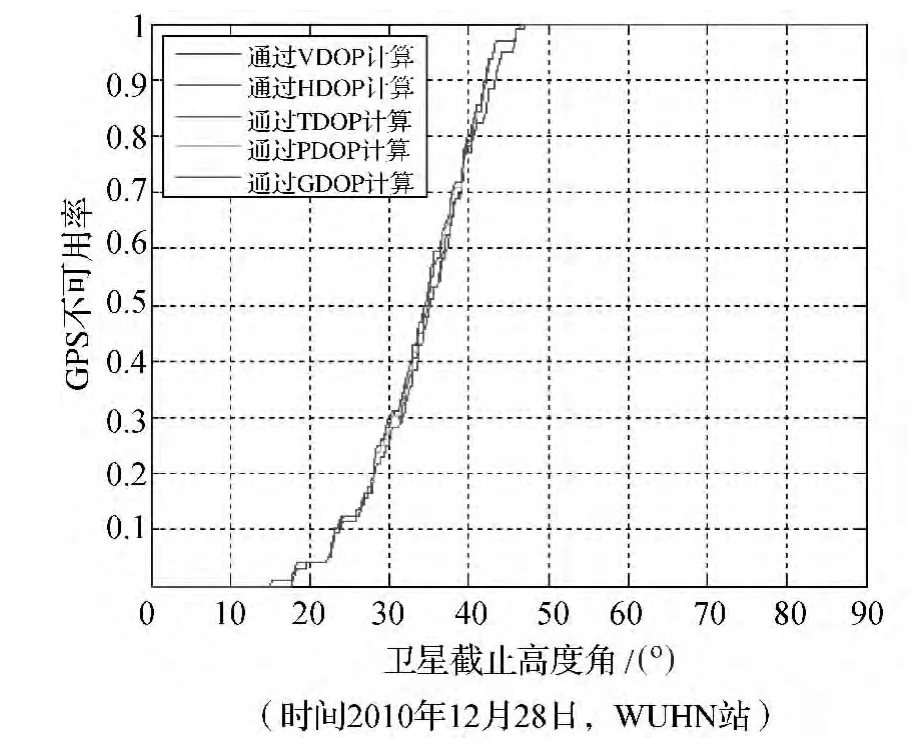
图4 5种DOP值计算得出的GPS卫星不可用率随卫星截止高度角的变化
在小波分析中,尺度函数φ(x)表示低频整体部分,小波函数ψ(x)表示高频细节部分,通常采用塔式Mallat算法进行小波分解和重构。设有离散信号,将其加载到尺度函数上得到,则 有 如 下 Mallat 算 法 卷 积 表达式[3]
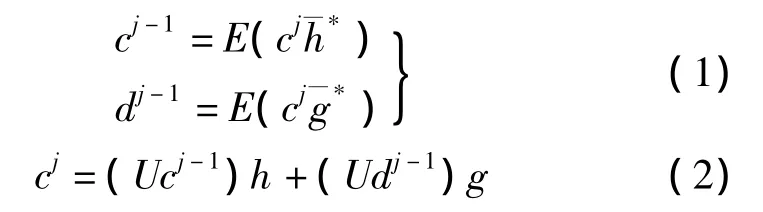
式1表示小波分解,式2表示小波重构。式中,cj-1表示分辨率2j-1上的近似信息;dj-1表示位于分辨率2j-1~2j之间的细节信息。
设长度为N的信号fn被噪声en污染,所测得的含噪数据为xn=fn+en。对含噪数据用Mallat算法进行分解,得到低频的整体部分和高频的小波部分[4]。对高频部分做阈值处理,阀值为
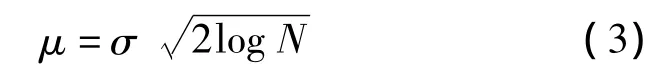
式中,μ为阈值;σ为估计的噪声标准差。
分解与重构结果如图5、图6所示(以GDOP为例)。
在经过小波变换后,由于卫星分布的不连续性等因素的影响,离散点阵的简单勾连所得到的曲线其变化仍然不是特别平滑,故需要对其进行拟合。根据上述小波重构得到的未拟合的概率分布函数可知,其在0—15°范围内不可用率为0,在50°以后不可用率累计保持为1。故在选择最优的拟合函数的时候除了需要考虑拟合函数与原函数残差较小外,还需要保证拟合函数的微分函数在0—15°和50°以上函数值近似等于0。根据上述条件,结合实际观测数据确定采用23阶多项式模型拟合该概率分布函数为最佳。拟合后的概率分布函数及其概率密度函数如图7、图8所示。

图5 小波分解
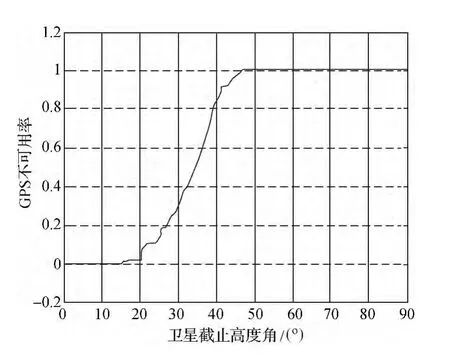
图6 一维小波重构

图7 拟合后的概率分布函数
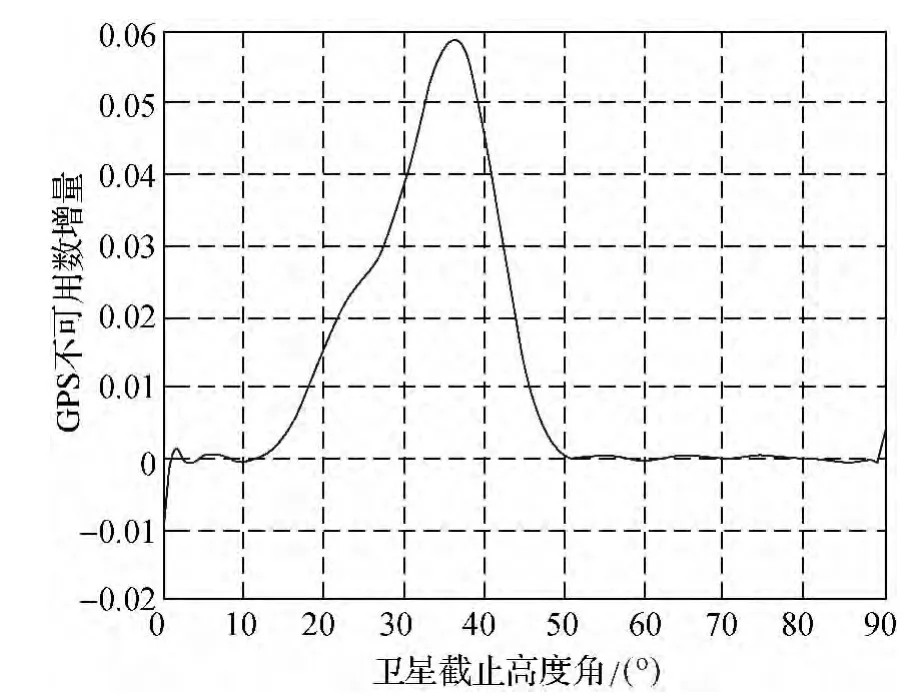
图8 概率密度函数
四、基于DOP值概率分布函数和概率密度函数的灵敏度分析
所谓灵敏度是指定位坐标分量的精度随着卫星高度角变化的变化率。而对定位坐标分量的精度进行衡量的指标即为各类值,故灵敏度可以理解为各类DOP值相对于角度变化量的变化率。如前所述DOP值在不加限制条件的情况下,其值随角度的增大而加速增大,以此计算出来的灵敏度也必将随着角度增加而增大,在90°时达到最大。但是这并没有现实的意义,因为一般高度角大于50°时即无法进行实际观测。所以本文设定了DOP值的阈值,并以此为基础统计不同高度角时DOP值超过阈值的百分比,即卫星的不可用率。然后通过研究卫星的不可用率随角度变化的概率分布函数及其概率密度函数,来间接确定卫星灵敏度随角度变化的规律。
根据上述在WUHN站以GDOP值计算所构建的拟合后的概率分布函数图像和概率密度函数可知:卫星在0—15°范围内全部可用,在50°以上完全不可用,故灵敏度均为0,对应的概率密度函数在该范围内也应趋近于0。在15—50°的范围内根据概率分布函数可知,卫星的不可用率显著增加,并在50°附近达到100%,根据概率密度函数可知卫星不可用率的增长率先增大后减小,在36.5°附近达到最大,故可认为GDOP值所对应的灵敏度在15°—50°的范围内先增大后减小,在36.5°附近最大。
通过上述分析可知在15°左右时开始出现不可用卫星,在36.5°左右定位坐标的整体精度(对应GDOP值)依赖于卫星高度角的灵敏度达到最大。所以在实际的工程应用中可以根据实际的观测条件和精度要求,设定不同的卫星高度角。根据上述结论,在要求整体精度最优的情况下,如果受到条件的限制而不能以0—15°范围内的高度角进行观测,接收机观测的截止高度角最大不应超过36.5°。
对全球8个IGS站应用上述模型,求出8个测站DOP值灵敏度最大值对应高度角,其结果见表1。
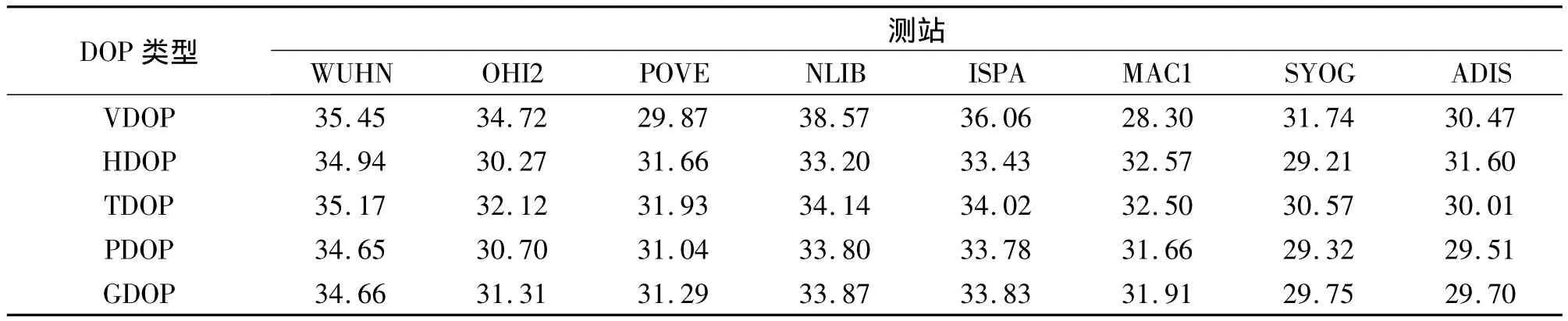
表1 全球多个测站的灵敏度最大值对应高度角(°)
由表1可知,各个站所定位坐标分量灵敏度最大值所对应的高度角有一定区别,但是基本上在30°以上。通过本文所建立的模型,输入测站对应的坐标即可计算出其灵敏度最大的高度角。在GPS外业测量时,如果卫星截止高度角高于30°,则测量误差会显著增大。测量时遇到遮挡应尽量使遮挡后产生的高度角低于30°,将会获得比较大的效益。
五、结束语
本文主要进行了定位坐标分量依赖于卫星高度角的灵敏度分析,提出了全角度区间衡量DOP值的统计的指标“GPS不可用率”,建立了5种DOP值之间的经验关系模型,并通过小波滤波、曲线拟合等方法成功获得GPS不可用率随截止高度角的变化及其概率密度函数,以此获得了定位精度灵敏度最大时所对应的截止高度角,并提出了GPS观测时的注意事项,可为GPS外业观测计划的制订提供参考。同时对比了多个IGS站应用该模型的结果,可知影响模型结果的因素与测站地理位置、卫星轨道整体布局的相对位置有关,这将作为后续研究的重点。
[1]HOFMANN W,LICHTENEGGER,WASLE.GNSS——Global Navigation Satellite Systems GPS,GLONASS,Galileo, and More[M]. Berlin:Springer, 2007:262-266.
[2]ELLIOTT D K,CHRISTOPHER J H,HEGARTY C J.Understanding GPS:Principles and Applications[M].2nd Ed.Norwood:Artech House,Inc,2005:334-343.
[3]MALLAT S G.A Theory for Multiresolution Signal Decomposition:the Wavelet Models[J].IEEE Trans on A-coustics,Speech and Signal Processing, 1987,37:2091-2110.
[4]李振,朱锋,陈家君.基于小波变换的桥梁风振变形监测数据处理[J].测绘通报,2011(11):18-20.
[5]成礼智,王红霞,罗永.小波的理论与应用[M].北京:科学出版社,2004:67-68.
[6]黄声享,刘经南,柳响林.小波分析在高层建筑动态监测中的应用[J].测绘学报,2003,32(2):104-107.
[7]LANGLEY R B.Dilution of Precision[J].GPS World,1999,10(5):52-59.
[8]SHARP I,KEGEN Y,GUOY J.GDOPAnalysis for Positioning System Design[J].IEEE Transactions on Vehicular Technology,2009,58(7):3371-3382.
[9]SRILATHA,G.SASI B R,S.Swapna R,et al.Investigation of GDOP for Precise User Position Computation with All Satellites in View and Optimum Four Satellite Configurations[J].The Journal of Indian Geophysical U-nion,2009,13(3):139-148.
[10]王泽民,孟泱,伍岳,等.GPS、Galileo及其组合系统导航定位的DOP值分析[J].武汉大学学报:信息科学版,2006,31(1):9-11.
