月面巡视探测器导航和全景相机标定方法研究
2014-12-12申振荣魏士俨刘少创
张 烁,申振荣,魏士俨,刘少创
(1.武汉大学测绘学院,湖北武汉430079;2.北京空间飞行器总体设计部,北京100094;3.中国科学院遥感与数字地球研究所,北京100101)
一、引 言
月面巡视探测器的立体视觉系统由6台相机构成。其中,包括一对导航相机、一对全景相机和一对避障相机,每对相机都是由设计参数相同的两台组成。对于月面巡视探测器来说,立体视觉系统的高精度标定与以下问题密切相关:①着陆器及月面巡视探测器的高精度定位与导航;②月面巡视探测器的高精度全局路径规划与生成机械臂运动策略;③着陆区及巡视探测区域的精细制图,提取高分辨率的DEM并生成正射影像。
为了满足深空巡视探测器立体视觉系统的高精度标定,国内外学者开展了一些研究,如Yakimovsky和Cunningham研究了CAHV和CAHVOR模型,并成功应用于美国“勇气号”与“机遇号”火星探测车的导航相机和全景相机标定;J.F.BellⅢ等提出了一种火星探测车的在轨实时标定算法;Donald B.Gennery针对美国火星探测计划提出了立体视觉系统的广义标定模型;在国内,王保丰等提出了月面巡视探测器避障相机的“两步法”标定算法[1-5]。
本文推导了一种基于自检校光束法平差模型的月面巡视探测器导航相机和全景相机的高精度标定算法。该方法采用附加畸变参数的针孔成像模型作为导航相机和全景相机的投影模型。首先,使用高精度平面格网作为标定物,在对平面格网进行旋转多角度拍摄后,采用模板匹配法高精度地提取格网点的像点坐标;此后,将格网点的像点坐标和空间坐标代入二维直接线性变换算子解算相机的内方位元素和像片的外方位元素初值,最后,将内、外方位元素初值、格网点的像点坐标和空间坐标代入严密的自检校光束法平差模型,对标定参数进行高精度迭代求解,当观测值的方差估值和未知数的改正值收敛于给定阈值后,解算出标定参数的精确值。
二、二维直接线性变换模型
月面巡视探测器导航和全景相机的标定参数包括相机的主点位置(x0,y0)、主距(fx,fy)、径向畸变(K1,K2)、切向畸变(P1,P2)、左相机相对于右相机的方位关系(ΔXs,ΔYs,ΔZs,Δφ,Δω,Δκ)。
利用二维直接线性变换算法可以解算出相机的内方位元素和像片的外方位元素初始值。二维直接线性变换模型可以表示为

式中,H=(h1,h2,h3,h4,h5,h6,h7,h8)T为二维直接线性变换的8个变换参数;X、Y为平面格网点的空间坐标(Z坐标为零);x、y为平面格网点的像点坐标。当每张像片中的格网点数大于4时,可以对式(1)进行线性变换解出8个变换参数的初始值;将式(1)进行泰勒级数展开,利用最小二乘方法迭代求解8个变换参数的精确值。
利用式(1)及摄影测量中的共线方程,可以推导出
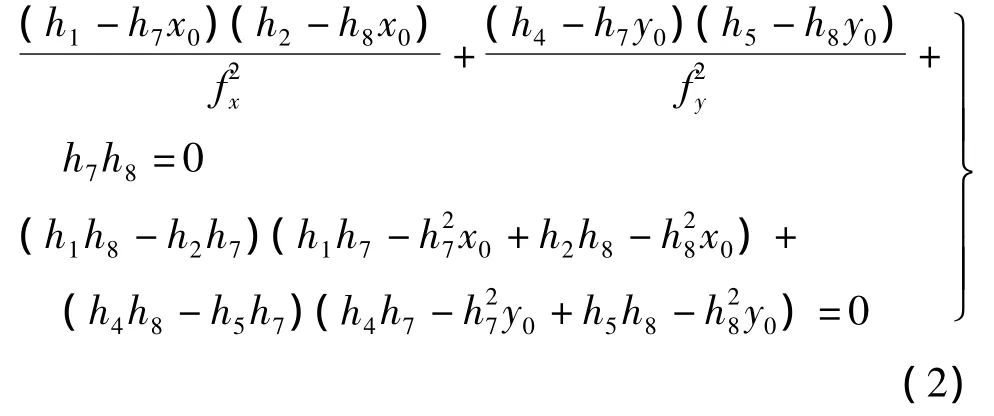
利用两张以上像片,将式(2)表示为LX=c的形式,通过解超定方程可以求得主距(fx,fy)和主点(x0,y0)的初始值。在解算过程中,要避免临界运动序列问题,即—相机固定而标定板只绕Z轴旋转,这时会造成8个参数之间线性相关。
在Y为主轴的转角系统下

通过式(4)求解像片外方位角元素,求解ω时,b3在开平方后首先取正号,将已确定的κ角与通过b3求得的 b1、b2算出的 κ'相比较,若 κ≠κ',则 b3取负号,然后重新计算b1、b2的值。
在解算出(φ,ω,κ)之后,需要重新计算旋转矩阵,像片外方位线元素(XS,YS,ZS)的初始值解算公式如下
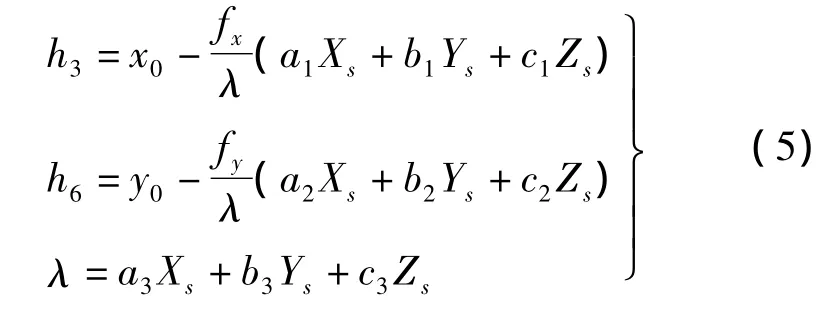
三、自检校光束法平差模型
利用严密的自检校光束法平差模型对标定参数的初始值进行迭代求解才能获得可靠且高精度的标定结果。引入径向畸变和切向畸变参数之后的共线方式如下[6]

式中,畸变模型表示为
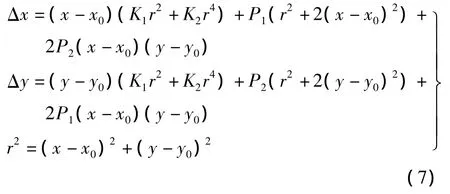
对式(6)进行泰勒级数展开,并将内方位元素、平面格网点空间坐标和畸变参数处理成虚拟带权观测值,则观测值的误差方程式表示为

式中,X1为外方位元素的改正数向量,A1为相应系数矩阵;X2为格网点空间坐标改正数向量,A2为相应系数矩阵;X3为内方位元素改正数向量,A3为相应系数矩阵;X4为畸变参数改正数向量,A4为相应矩阵;L1为像点坐标的观测值向量;E2、E3、E4为单位矩阵;P1、P2、P3,P4为对应观测值的权矩阵。
式(8)是典型的间接平差公式,误差方程式中各展开项的系数可见参考文献[7],其对应的法方程式可表示为[8]

对于自检校光束法平差模型,各观测值权的大小决定了待解算参数的精度和未知数的收敛程度,因此要对各观测值赋以合适的权值[9-10]。本文采用验后方差估计的方法对观测值赋权,观测值的权矩阵可用以下公式计算
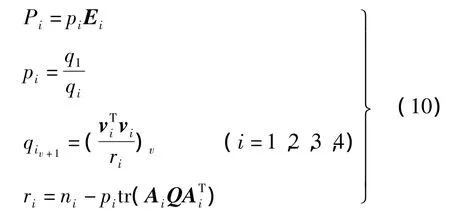
式中,qi为第i组观测值的方差估值;vi为第i组观测值的改正数向量;ri为第i组观测值的多余观测分量;v为迭代次数;Ai为第i组观测值在误差方程式系数阵中之相应子矩阵;ni为第i组观测值个数;Q=(ATPA)-1,为未知数的协因素阵。
通常均假设p1=1,迭代计算的收敛标准可用表述,ε1为极小值。
四、算法试验与分析
对于上文提出的月面巡视探测器导航和全景相机标定算法,采用一组实际数据进行试验。平面标定格网大小为400 mm×300 mm,共88个设计格网点,格网间距30 mm,格网点精度0.2 mm。试验采用的CCD相机的视场角为15°×15°,将两台CCD相机固定在约270 mm的基线上,构成月面巡视探测器立体视觉系统,如图1所示。
拍摄标定影像时,控制立体视觉系统的两台相机在标定格网前方0.7 m处的9个位置同时进行拍摄,左右两台相机在每个摄站都拍摄0°和90°两张影像,共获取36张标定试验影像。

图1 月面巡视探测器立体视觉系统示意图
采用基于模板匹配的算法对格网点的像点坐标进行精确提取,像点坐标提取精度达到0.1像素,匹配格网点如图2所示。利用严密的自检校光束法平差模型将格网点的设计坐标作为未知数,并赋予适当的权值进行平差,以精确求解出左右两台相机的标定参数及格网点空间坐标,标定的统计结果见表1;左相机相对于右相机的方位关系见表2。

图2 匹配格网点示意图

表1 立体视觉系统标定统计结果 像素

表2 左相机相对于右相机的方位关系
为了评价本文提出的月面巡视探测器立体视觉系统标定算法的精度,统计了平差结果中各项参数的中误差,见表1。
利用自检校光束法平差进行月面巡视探测器立体视觉系统标定的单位权中误差在0.2个像素左右。将标定参数、像片的外方位元素及平差后的格网点空间坐标带入式(6),计算出格网点的像点坐标与模板匹配方法获取的格网点像点坐标差值的中误差。月面巡视探测器立体视觉系统左、右相机拍摄的每张像片中像点坐标的匹配值和投影值差值的中误差在1个像素左右。因此,利用本方法可以对月面巡视探测器的导航和全景相机进行高精度的标定。
五、结束语
本文详细推导了一种适用于月面巡视探测器导航相机和全景相机的高精度标定算法。采用一对工业镜头模拟了月面巡视探测器全景相机和导航相机,并利用一组实际数据对算法进行试验验证,试验证明本算法具有较高的精度和灵活性,可以满足月面巡视探测器导航相机和全景相机高精度标定的要求。
在利用法方程式(BTPB)X=BTPL求解未知数的改正数X时,由于方程式的系数矩阵过大(通常为上千阶的方阵),导致求解效率低下,因此需要对法方程的系数矩阵进行优化处理,以提高求解速度,这将在后续研究中予以关注。
[1]GENNERY D B.Generalized Camera Calibration Including Fish-eye Lenses[J].International Journal of Computer Vision,2006,68(3):239-266.
[2]MAKI J N,BELL J F,HERKENHOFF K E,et al.Mars Exploration Rover Engineering Cameras[J].Journal of Geophysical Research,2003,108(E12):8071.
[3]YAKIMOVSKY Y,CUNNINGHAM R.A System for Extracting Three-dimensional Measurements from a Stereo Pair of TV Cameras[J].Computer Graphics and Image Processing,1978,7(2):195-210.
[4]BELL J F,SQUYRESS W,HERKENHOFF K E,et al.Mars Exploration Rover Athena Panoramic Camera(Pancam)Investigation[J].Journal of Geophysical Research,2003.108(E12):8063.
[5]王保丰,毛晓艳,唐歌实.月球车鱼眼相机的标定方法研究 [J].宇航学报,2011,32(4):934-939.
[6]刘少创,贾阳,陈建新.月面巡视探测器立体相机共线方程的建立[J].航天器工程,2007,16(3):17-20.
[7]张永军,张祖勋,张剑清.利用二维DLT及光束法平差进行数字摄像机标定[J].武汉大学学报:信息科学版,2002,27(6):567-571.
[8]詹总谦,张祖勋,张剑清.基于稀疏矩阵技术的光束法平差快速算法设计[J].测绘通报,2006(12):5-8.
[9]李德仁.自检校光束法区域网平差中的验后权估计[J].武汉大学学报:信息科学版,1982,7(1):16-24.
[10]李德仁,FORSTNER W.附加参数的可靠性研究[J].测绘学报,1987,16(2):103-111.
