附有限制条件的间接平差的求解方法探讨
2014-12-12李爱国胡圣武
李爱国,胡圣武
(1.长安大学地测学院,陕西西安710054;2.河南理工大学 测绘学院,河南焦作454000)
一、引 言
附有限制条件的间接平差模型是5种平差模型之一,对其计算公式有严密的推导[1-3]。不过附有限制条件的间接平差的公式相对于条件平差、间接平差等平差模型而言,其计算公式比较复杂,不易掌握。因此,应探讨用一种比较简单的方法来求解。
二、现有附有限制条件的间接平差的求解方法的简述
附有限制条件的间接平差的数学模型为

按照最小二乘准则,要求VTPV=min,可求得如下公式
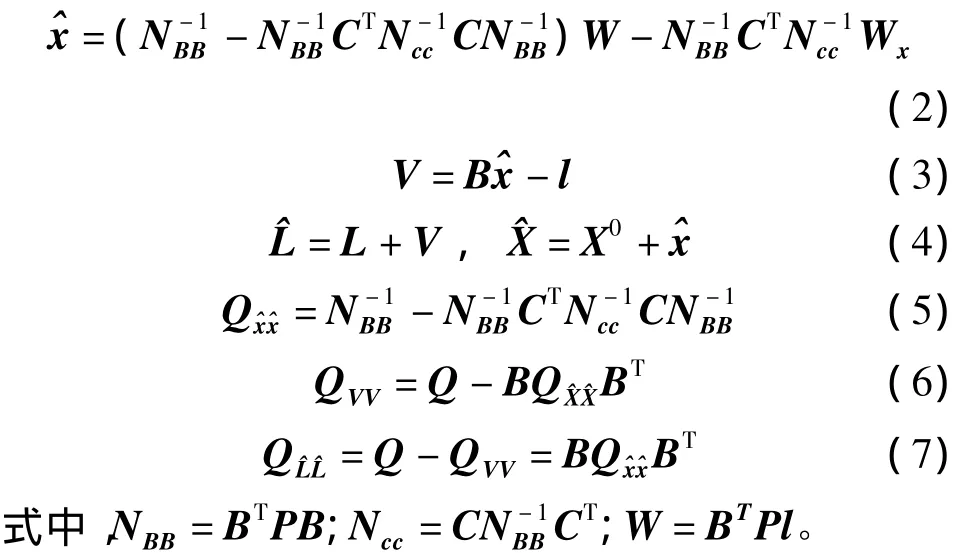
这就是附有限制条件的间接平差的主要计算公式,具体推导可参阅相关的教材[1,4-6]。
三、新的附有限制条件的间接平差的方法的求解原理
新方法的实质就是消除限制条件方程,把附有限制条件的间接平差模型转换为间接平差来求解,主要有3个步骤。
1.确定独立参数的个数,并把非独立参数表达成独立参数的函数
如果限制条件方程是非线性方程,则把非独立参数化为独立参数的线性表达。
2.消除限制条件
把非独立参数代入条件方程中,则限制条件就不存在了,达到了消除限制条件的目的,从而得到了新的条件方程

3.间接平差求解
消除限制条件后,则附有限制条件的间接平差模型就转化为间接平差模型,按间接平差模型来求解,从而达到计算简单的目的。
四、实例分析
下面通过举例来说明本方法的结算过程。
如图1所示,将一个大矩形分为两个小矩形(设各角度均为90°)。下列观测值等权且相互独立:L1=2.00 m,L2=3.00m,L3=1.00m,L4=4.10 m,L5=1.94 m。若有强制附合条件S1=3S2,试计算面积S1及S2的最小二乘估值及其权倒数。

图1 矩形示意图
解:本题由于有强制附合条件,则可选用附有限制条件的间接平差模型,设L1、L2、L3的平差值为参数并取
由于必要观测数t=2,所选参数u=3,参数之间不独立,非独立参数个数为1,观测数为5,则误差方程数c=5,限制条件方程个数s=1。
列出误差方程和限制条件方程为
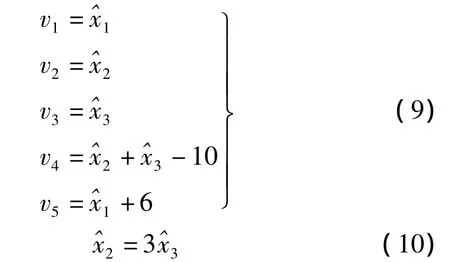
1)确定独立参数,并把非独立参数表示成独立参数的函数。由于所选参数为3个,参数之间相关,选^x1和^x3作为独立参数,把^x2表示成^x1和^x3的函数,根据式(10)可得

2)消除限制条件。将式(11)代入式(9)可得
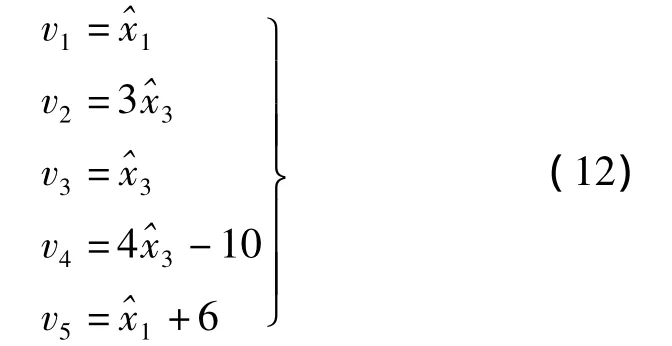
3)按间接平差求解,根据式(12)可得

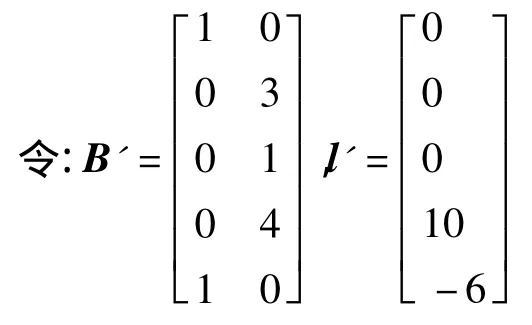
由于观测值是等权且独立,则其随机模型为

则有
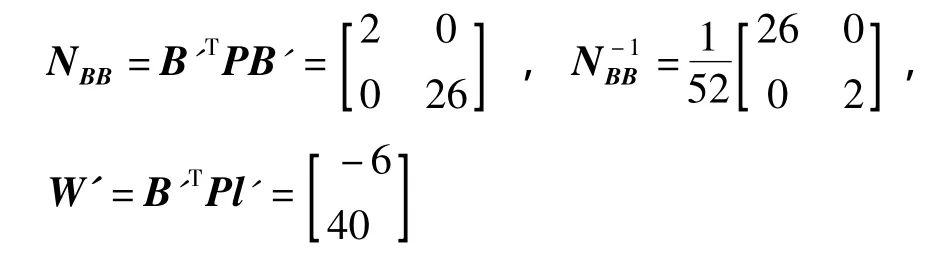
根据式(13)和式(14),按间接平差可求得

根据式(11)可得

根据式(13)可得
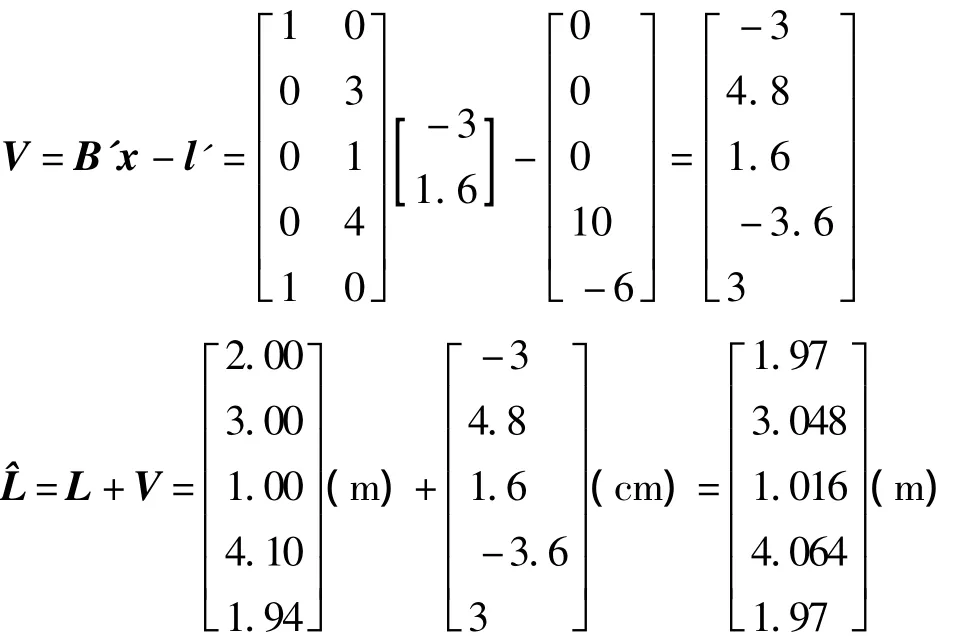
因此有
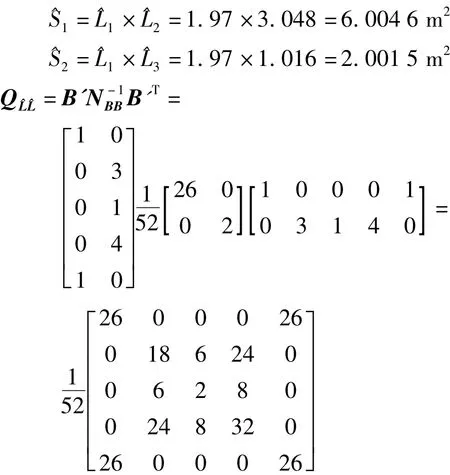
由于

得

因此有

同理得
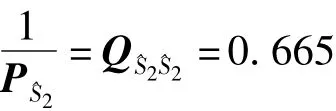
以上计算就是用新方法的计算过程,下面就本例用附有限制条件的间接平差模型进行计算。
根据附有限制条件的间接平差模型,可以列出式(9)和式(10)的条件方程和限制条件方程。随机模型与上述一样。
则有
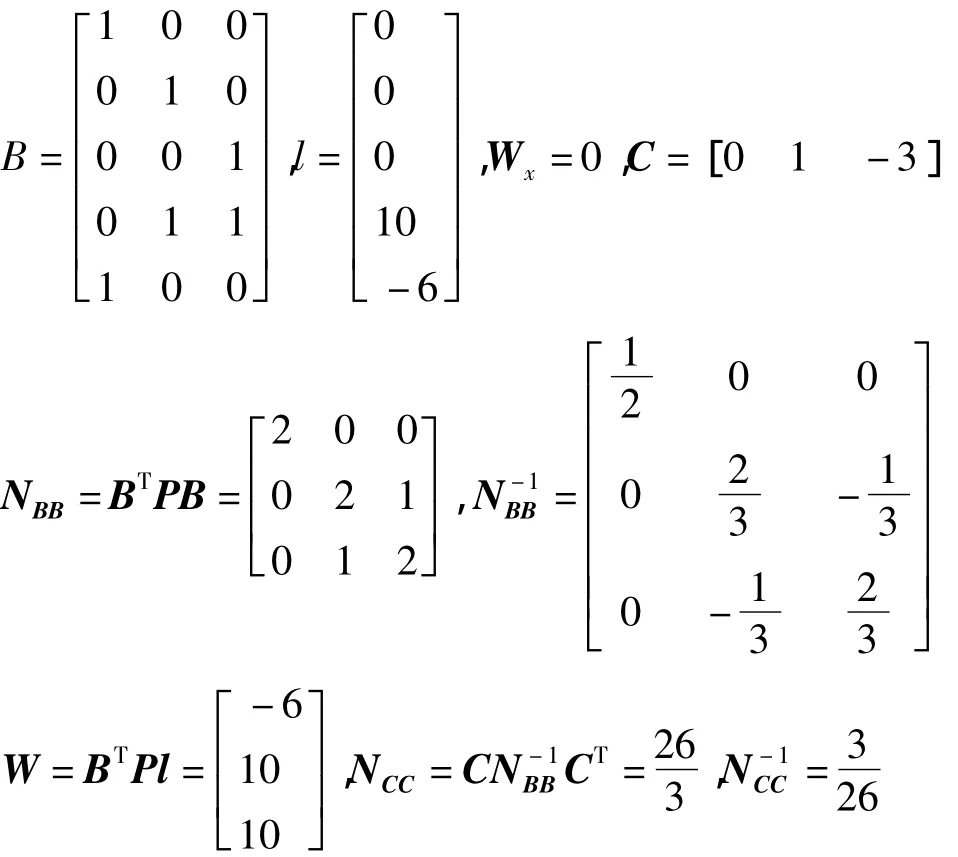
根据式(2)可得
根据式(3)可得
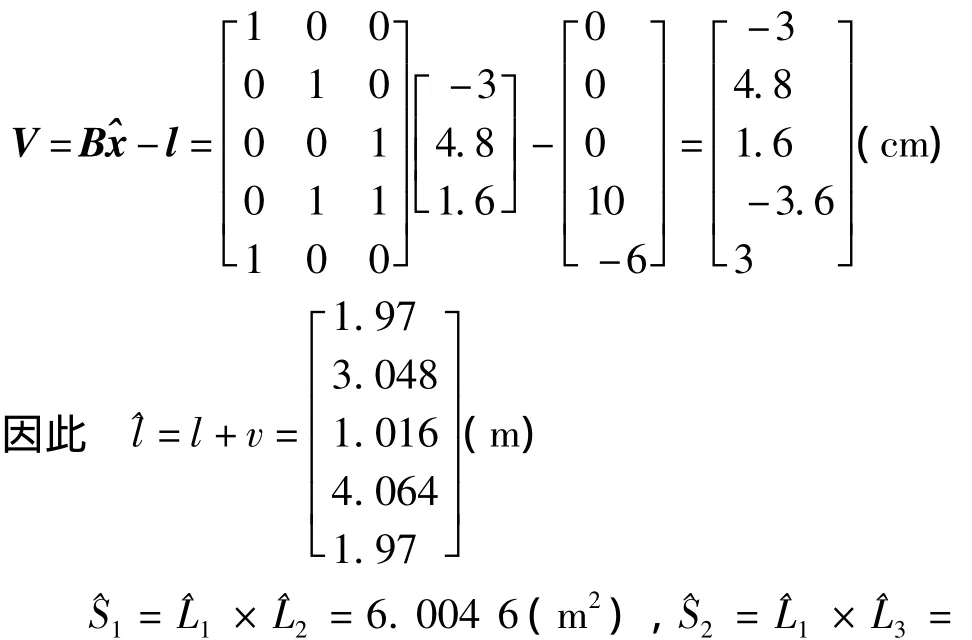
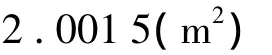
根据式(7)可得
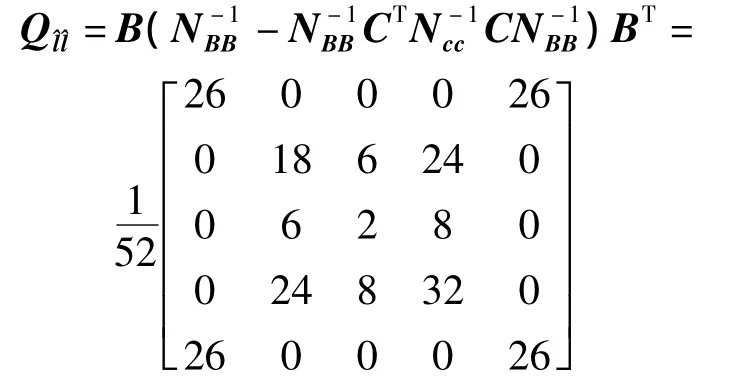

可见,两种方法求算的结果完全一致,说明两种方法是等价的,也证明了所提出方法的正确性和科学性。
五、结束语
附有限制条件的间接平差的计算公式及公式的推导都比较繁琐,这给平差的学习带来不利的影响,完全可以用间接平差取代。目前有很多学者在其著作中已经把附有限制条件的间接平差不作重点介绍是科学的和合理的[7-10]。
[1]胡圣武,肖本林.误差理论与测量平差基础[M].北京:北京大学出版社,2012.
[2]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].2版.武汉:武汉大学出版社,2009.
[3]王穗辉.误差理论与测量平差基础[M].上海:同济大学出版社,2010.
[4]金日守,戴华阳.误差理论与测量平差基础[M].北京:测绘出版社,2011.
[5]隋立芬,宋力杰,柴洪洲.误差理论与测量平差基础[M].北京:测绘出版社,2010.
[6]葛永慧,夏春林,魏峰远,等.测量平差基础[M].北京:煤炭工业出版社,2007.
[7]陶本藻,邱卫宁.误差理论与测量平差[M].武汉:武汉大学出版社,2012.
[8]赵超英,张勤.再论经典测量平差模型间的内在联系[J].测绘通报,2006(3):26-27.
[9]邓永和.《再论经典测量平差模型间的内在联系》的研究[J].铁道勘察,2009(2):8-10.
[10]张俊,张鹏飞.测量平差课程教学改革探讨[J].测绘科学,2010,35(5):247-249.
