基于Archard理论分析弹体质量侵蚀＊

郭 磊，何 勇，张年松，庞春旭，郑 浩

（南京理工大学智能弹药技术国防重点学科实验室，江苏 南京210094）

动能弹侵彻混凝土过程中，弹体的质量侵蚀现象是一个十分复杂的物理问题。早期研究中，弹体侵彻速度较低，为了理论分析方便，常假设弹体为理想刚性体，然而，随着侵彻速度的提高（＞1km／s），弹体的侵蚀效应变得显著［1－3］，该刚性假设已经不再成立。同时，混凝土材料的非均质特点导致弹体在侵彻过程中受力不对称，可能导致侵彻弹道弯曲或弹体结构破坏等情况，从而使弹体的质量侵蚀更严重，对侵彻能力的影响更明显。因此，研究高速侵彻混凝土过程中弹体的侵蚀效应具有重要意义。

弹体的质量侵蚀现象最早由M.J.Forrestal等［1］在研究动能弹侵彻混凝土靶的实验中发现，质量损失率高达（7～12）%。D.J.Frew等［4－5］开展了不同材料和几何形状的高强合金钢质尖卵形弹体的侵彻实验，获得了不同撞击速度下的侵彻深度和弹体质量损失率。何翔等［2］、杨建超等［3］也开展了弹体高速侵彻混凝土的实验，发现熔融和磨损是导致弹体质量侵蚀的主要原因。S.A.Silling等［6］拟合大量实验结果，发现弹体侵彻后的质量损失百分比与弹体的初始动能存在线性关系。陈小伟等［7］发现弹体动能和混凝土骨料硬度对弹体的侵蚀效应有显著影响。S.E.Jones等［8］和R.N.Davis等［9］假设侵彻中摩擦功全部作用于弹体，且弹体质量损失来源于弹头表面材料的熔化脱落，得到了质量损失的计算表达式。J.R.Klepaczko等［10］通过模拟弹靶接触面上的微观凸起断裂来分析摩擦因数的变化。L.Guo等［11］对比高速侵彻前后弹体表面材料细观组织变化提出了受影响区的3个组织分区。何丽灵等［12－14］通过总结S.E.Jones等［8］和S.A.Silling等［6］的工作，得到了影响弹体质量侵蚀量的7个重要参数，并编程模拟了侵彻过程中弹头形状的演化。郑浩等［15］利用数值模拟的方法对比分析了弹体刚性侵彻和考虑侵蚀效应的侵彻过程。杨阳等［16］、Mu Zhong－cheng等［17］、赵晓宁等［18］通过修正质量损失百分比与弹体初始动能的线性关系，提出了计算弹体侵蚀的工程钝化模型。目前，大部分关于弹体质量侵蚀的研究是基于实验数据的经验公式或半经验半理论方法，或者简单假设摩擦力所做的功全部作用于弹体，弹体材料熔化而产生质量损失，在高速条件下，其预测结果可能与实际不符，且不能很好地预测新工况下的弹体侵蚀情况。

本文中，基于模具与工件磨损的相关研究［19－21］，结合侵彻混凝土过程中弹体表面高温、高压、高应变率的特殊环境，采用从弹体微粒的细观塑性变形到宏观质量损失的分析方法，提出了一种基于Archard粘着磨损理论的弹体质量侵蚀表征模型，得到了弹体侵蚀速度，其大小与弹靶表面法向应力以及切向速度等因素有关。在一定假设条件下，通过差分计算，得到了弹体的外部轮廓演化情况，并且分析了弹体质量侵蚀效应对侵彻深度的影响，计算结果与实验结果吻合较好。

1 Archard磨损模型简介

J.F.Archard等［19－20］和J.T.Burwell等［21］在对模具与工件的磨损深入研究的基础上提出了粘着磨损理论，即2个光滑表面接触作用，其真实接触面存在于大量微凸起（微米量级）上，由于局部应力集中，微凸起会发生塑性变形。设两接触微凸起为一对半径相同的半球形且半径为a，如图1所示，上微凸起材料较脆弱，其硬度为H，该对微凸起所受法向载荷为δF。根据材料硬度的定义，则该对微凸起塑性变形后的接触面积为δA＝πa2＝δF／H。

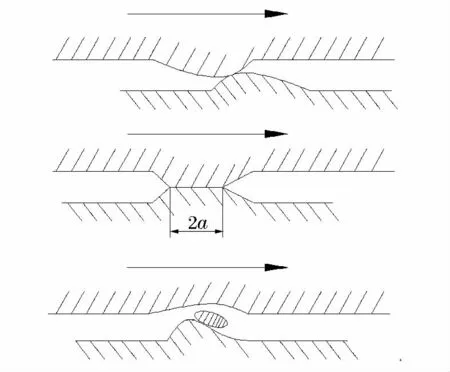
图1 粘着磨损理论的简化模型Fig.1 Asimplified model for the adhesive wear theory

设一次滑动产生一个磨损体积为δVL的颗粒。物理实验显示，磨损颗粒的形状是等轴的，因而半球形微凸起的体积为δVL＝2πa3／3。假设这对微凸起滑动摩擦持续的行程δL为最长滑动行程模式，则δL＝2a。可以求得单位行程的磨损体积为：

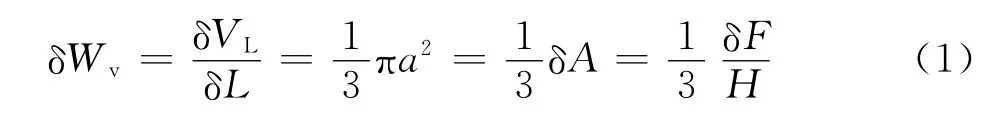
对于整个接触平面来说，可得磨损量为：

式中：K1为比例常数，引入的原因是一次摩擦中产生一个磨损颗粒的假设与实际不符。取K＝K1／3，同时，dWv＝dVL／dL，载荷dF用dp表示，可得到用于模具磨损的Archard模型公式：

式中：dVL为磨损体积，dp为工件与材料接触表面的法向压力，dL为工件与模具之间的切向相对滑移距离，H为模具硬度；K为磨损因数，与K1具有相同的物理意义，代表一对微凸起相互摩擦产生一个微凸起磨损颗粒的可能性［19］。研究表明，磨损因数K在不同典型实验情况下相差很大。由式（3）可知：磨损量与摩擦行程和法向载荷成正比，与较软材料的表面硬度或强度成反比。

2 弹体质量侵蚀模型

研究弹体高速侵彻过程中的侵蚀效应，需要充分理解弹体与靶体的相互作用。弹体高速侵彻混凝土的过程中，弹体处于高温、高压、高应变率状态。由于侵彻过程时间短（微秒量级），热量来不及扩散，集中在弹体表面薄层，导致弹体材料的性能发生变化。当高应变率下的温升对材料的软化效应大于应变硬化效应时，弹体材料表面微粒出现塑性变形，即该微粒会产生塑性流动并存在流动速度，这里称之为弹体侵蚀速度va，方向沿弹头表面内法线方向。在细观尺度上，磨损微粒是由混凝土微粒对弹体微粒切削磨损和热熔化造成的，最终导致宏观上弹体的质量损失，这与Archard磨损理论中简化模型的条件相似。

将Archard公式进行变换，左边dVL＝dAdh，右边dp＝σndA，dL＝vtdt，其中dA为磨损微粒面积，dh为磨损深度，σn为靶体作用在弹体表面上的法向应力，vt为切向相对速度，dt为弹靶间单位作用时间，弹体头部表面受力如图2所示。在弹体高速侵彻条件下，用Kp代替磨损因数K，代入式（3）化简得到弹体侵蚀速度：

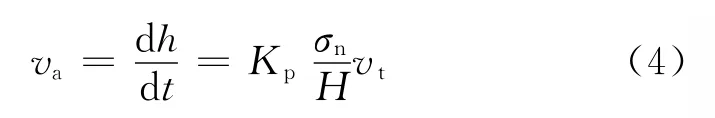
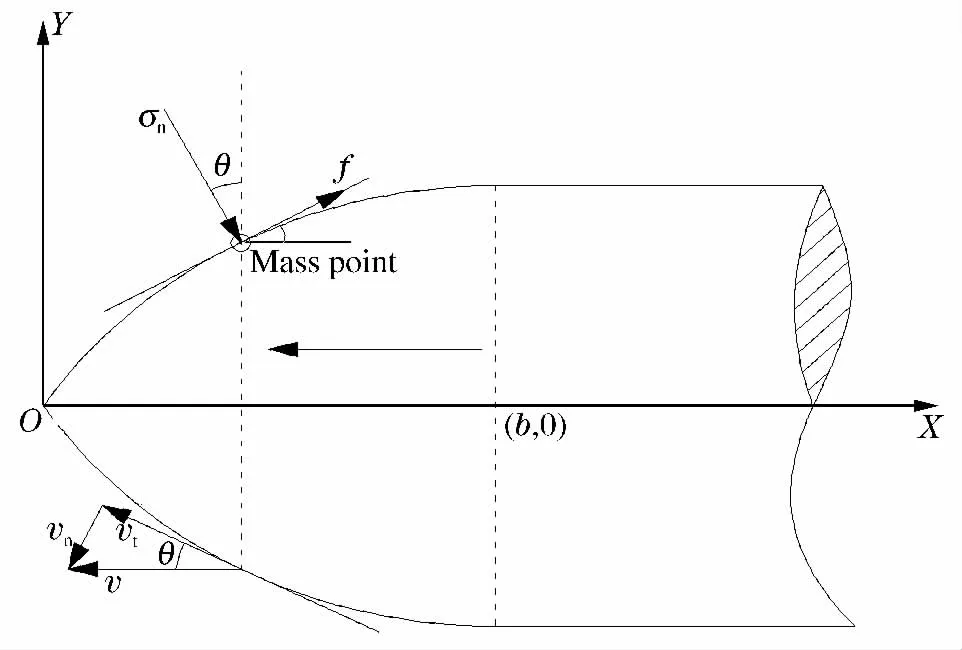
图2 弹体头部表面受力Fig.2 Forces on the nose of the projectile

式中：Kp为弹体侵蚀因数。

由式（4）可知，弹体质量损失与弹体侵蚀因数、所受的法向应力、相对运动速度以及材料的硬度有关。对 He Li－ling等［13］提出的影响弹体质量损失的7个参量（分别为弹体初始撞击速度、初始头形、熔化热、弹径、靶体密度、无约束抗压强度和骨料莫氏硬度）进行分析，同时对比式（4），可以推断弹体侵蚀因数Kp与弹材的屈服强度、热相关因数、混凝土靶的抗压强度、骨料硬度和撞击条件等有关。为了更清晰地反映弹体强度对质量侵蚀的影响，将硬度H用弹体材料的屈服强度Yp表示，则侵蚀速度va的表达式为：

在Archard公式中，J.T.Burwell等［21］研究发现，在一定的接触压力内，磨损因数K与压力p成正比，超出一个阈值（H／3）后，K成指数形式增长，如图3（a）所示。考虑到侵彻中弹体侵蚀问题与工件磨损的相似性，假设弹体侵蚀因数Kp与法向应力σn之间具有相同的变化趋势，在式（5）中，侵蚀因数Kp表征弹体受侵蚀的剧烈程度，在相同的弹靶条件下，假设Kp只与σn有关，在σn达到弹体材料的阈值（Yp／3）前，Kp为定值K0，超过阈值后，Kp随σn的增大而增大。为了简化计算，认为Kp与σn成线性关系（如图3（b）所示）：

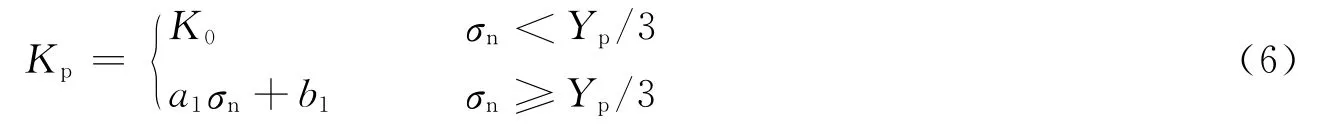
式中：a1、b1的具体值可通过实验数据确定。在不同弹靶条件下，其相应的a1、b1也将不同。

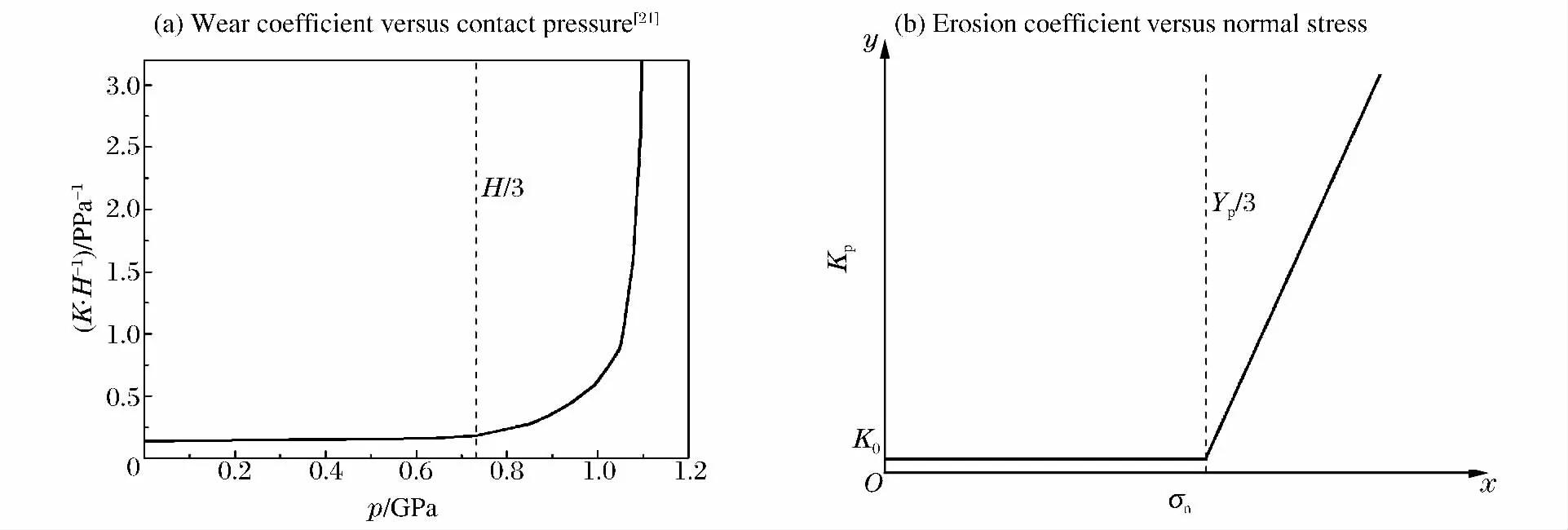
图3 磨损因数与侵蚀因数的相似性Fig.3 Similarity between wear coefficient and erosion coefficient

3 差分计算

为了表征弹体头部表面离散点的运动，需要在弹体上建立相对坐标系XOY，以弹尖为原点O，弹头部长为b，弹体总长为l，半径为r，曲径比为ψ。将整个弹体按轴向长度为lc离散为有限多个微小段，通过研究每个离散点的运动情况，来模拟整个弹体外形轮廓的变化，从而得到弹体的侵蚀情况，如图4所示，下标j表示第j个离散点。由于开坑阶段时间短，开坑过程中对弹体做刚性处理［12］。

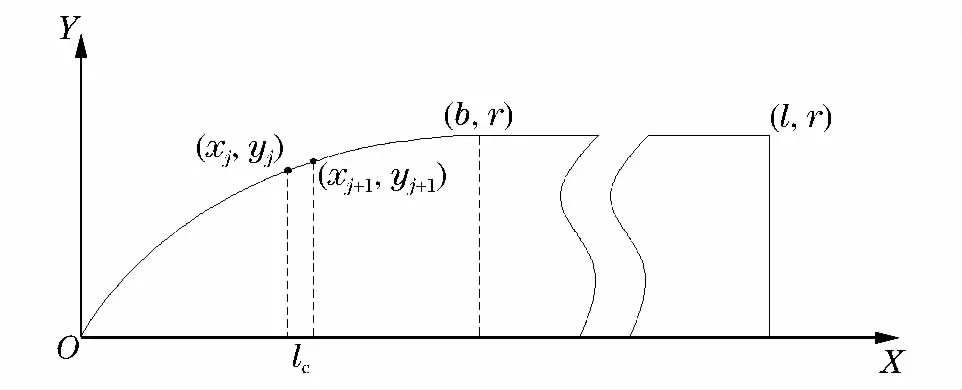
图4 弹体的离散情况Fig.4 The dispersion of the projectile

将整个侵彻过程离散成有限个微小时间步，假设在每个微小时间步Δt内，弹体轴向方向上所受到的载荷（加速度ax）不变。上标i表示第i个时间步，可知：

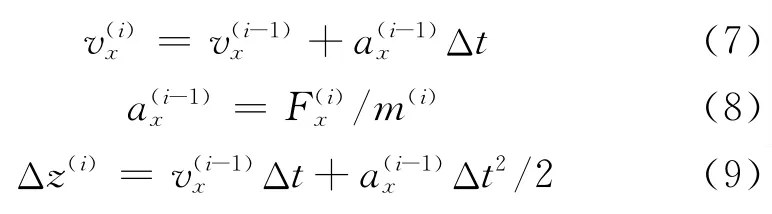
式中：vx、ax和Fx分别为弹体轴向的瞬时速度、瞬时加速度和瞬时阻力，m为弹体的瞬时质量，Δz为单个时间步内弹体的行程。为了准确地计算离散质点的运动情况，假设：（1）弹体正侵彻混凝土靶；（2）弹体表面轮廓均受到侵蚀作用；（3）由于弹体表面受力轴对称分布，侵蚀回退轴对称，计算简化为二维模型；（4）摩擦力为零；（5）侵彻过程中，弹体密度恒定不变。

如图5所示，为求弹体在第i时刻的头部轮廓，在已知第i时刻的弹体轴向速度v（i）x时，有：

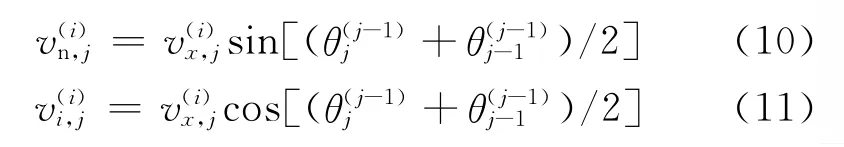
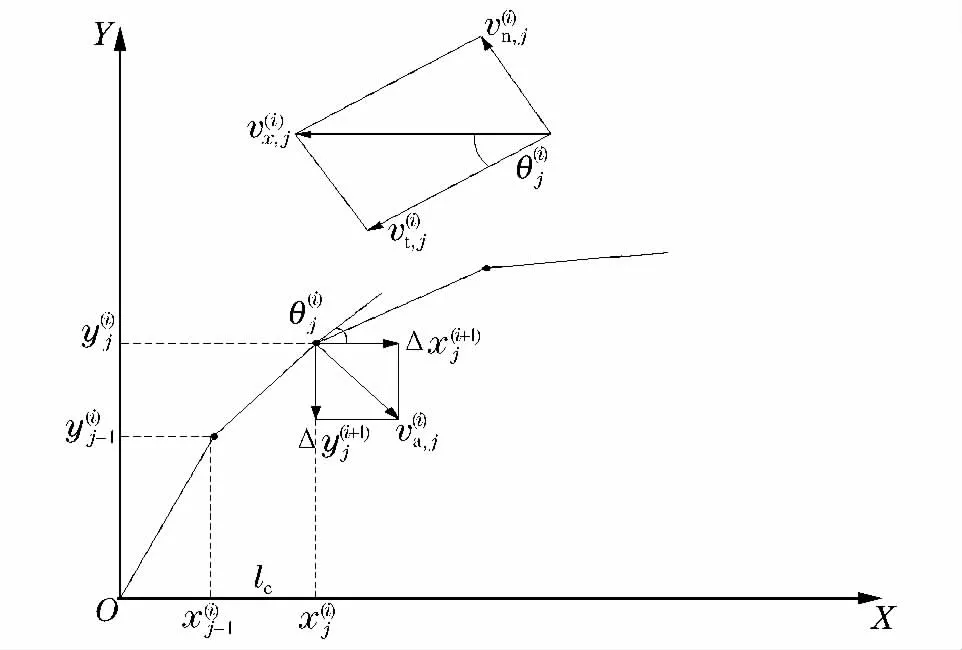
图5 第i步时弹体上第j个质点的运动情况Fig.5 The movement of node j at step i

式中：vn、vt分别为弹体轴向速度沿表面轮廓法线和切向方向的分量。将混凝土看成均质材料，靶体对弹体的作用用响应函数代替，由 M.J.Forrestal等［22］提出的动态空腔膨胀理论，得到靶体响应函数表示为：

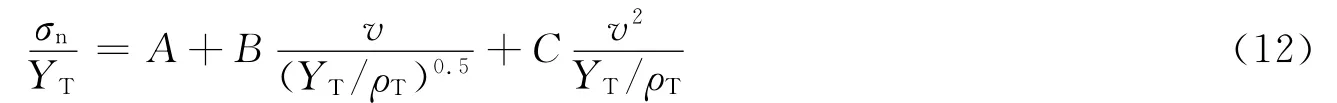
式中：YT、ρT分别为混凝土无围压抗压强度和混凝土密度；v＝vxsinθ为空腔膨胀速度；参数A、B、C可通过拟合得到，与混凝土材料有关。

联立式（5）～（6）、（11）～（12）得到i时刻j点的坐标：

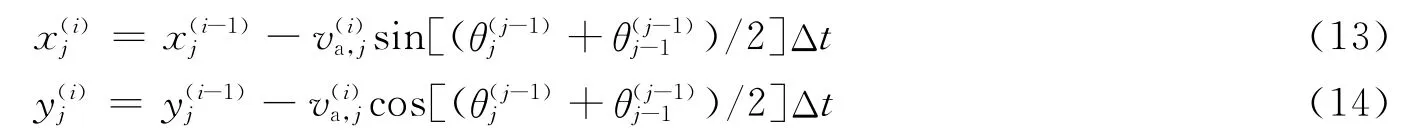
从而得到下一个时间步的初始计算参数：

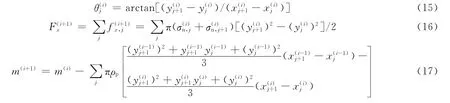
如此循环，直至弹体轴向速度vx减小到零，停止计算。

4 计算结果与分析

以M.J.Forrestal等［1］实验中工况4的条件进行计算，其中弹体材料为4340钢，弹体材料密度ρp＝7.81t／m3，直径D＝30.5mm，屈服强度Yp＝1 481MPa，曲径比ψ＝3，初始质量m0＝1.6kg，长径比为10。靶体为石英骨料素混凝土，密度ρT＝2.3t／m3，无围压抗压强度YT＝51MPa，根据撞击速度为405m／s下试算确定式（6）中参数K0＝0，a1＝－6.39kPa－1，b1＝1.42×10－11，由混凝土参数拟合得到式（12）中参数A＝9.72，B＝0，C＝1。

为分析侵蚀效应对弹体侵彻能力的影响，表1将侵蚀模型和刚性模型的计算结果与实验结果进行对比，其中刚性模型是令弹体表面质点的侵蚀速度为零时得到的计算结果。由表1可以看出，该侵蚀模型能较准确地计算弹体在高速条件下的侵彻深度P和质量损失百分比εm。侵蚀模型计算得到的弹体质量损失百分比随撞击速度vs的增大而增大，与实验结果吻合较好。与此同时，刚性模型计算得到的侵彻深度在低速条件下与实验结果基本吻合，但是在高速条件下，刚性模型计算误差也随之增大。可见，高速条件下的侵彻问题必须考虑弹体的侵蚀效应，弹体侵蚀效应对侵彻深度的影响随着撞击速度的增大而增强。

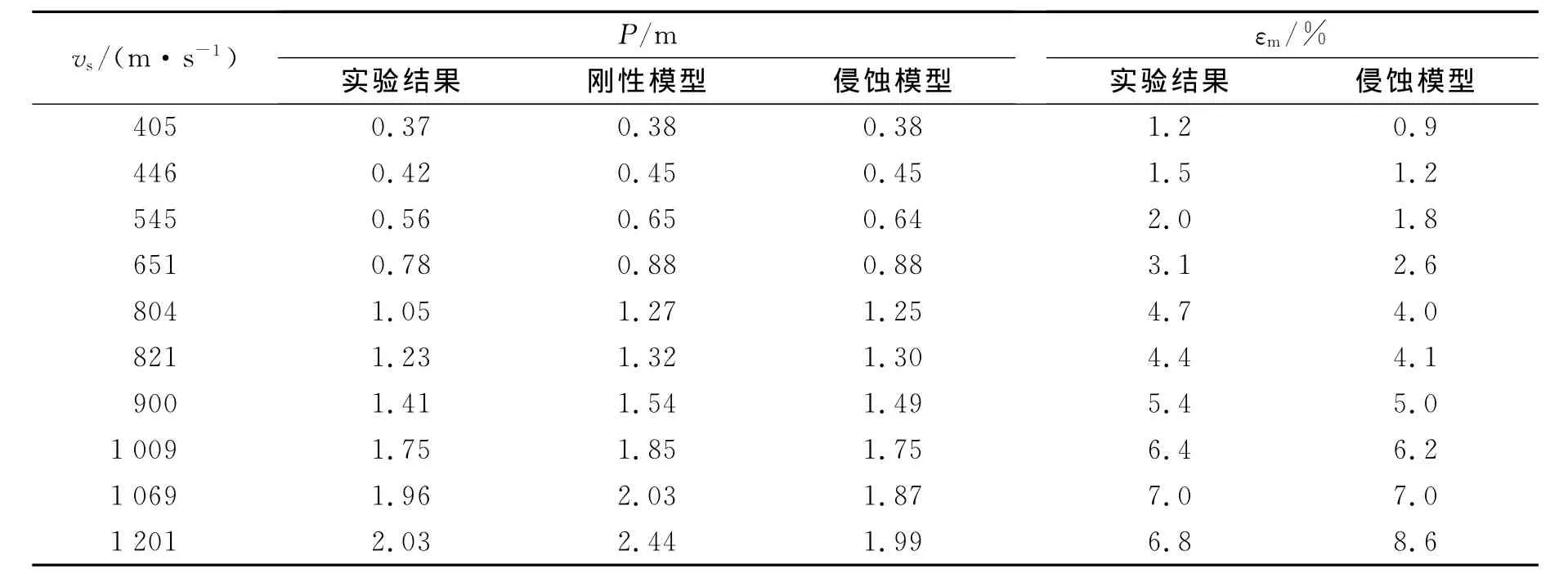
表1 侵蚀模型和刚性模型的计算结果与实验结果的对比Table 1 Comparisons among erosion model results，rigid model results and experimental results

弹体侵彻过程中各表征参数随时间的变化如图6所示，这里选取撞击速度分别为651和1 201m／s进行分析。通过对比发现：考虑弹体侵蚀效应时的侵彻过程与刚性弹有较大不同，当撞击速度较低时（651m／s），侵蚀效应不明显，对侵彻过载G、侵深和速度的影响都较小，可忽略不计。但是，在撞击速度较高时（1 201m／s），侵蚀效应变得显著，与刚性模型计算结果相比，侵彻时间变短，侵彻深度降低。如图6（a）所示，在1 201m／s的撞击速度下，弹体侵彻最大过载较刚性条件下有较大提高（约11%），且最大过载出现在开坑段结束后、稳定侵彻段的初始阶段。这是由于弹体侵蚀效应改变头部外形，在较高的撞击速度下，导致靶体响应函数值增大造成的。该结果可为高速侵彻条件下战斗部设计中装药过载问题的计算提供了一定参考。

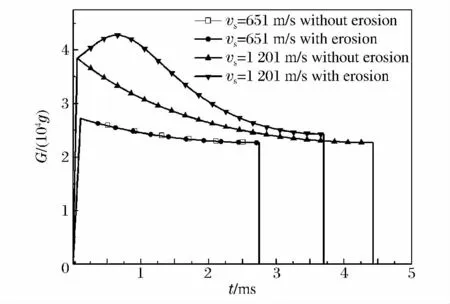
图6 （a）弹体侵彻过程中加速度的时间历程曲线Fig.6 （a）Deceleration of the projectile versus time during penetration

图6 （b）弹体侵彻过程中侵彻深度的时间历程曲线Fig.6 （b）Penetration depth of the projectile versus time during penetration

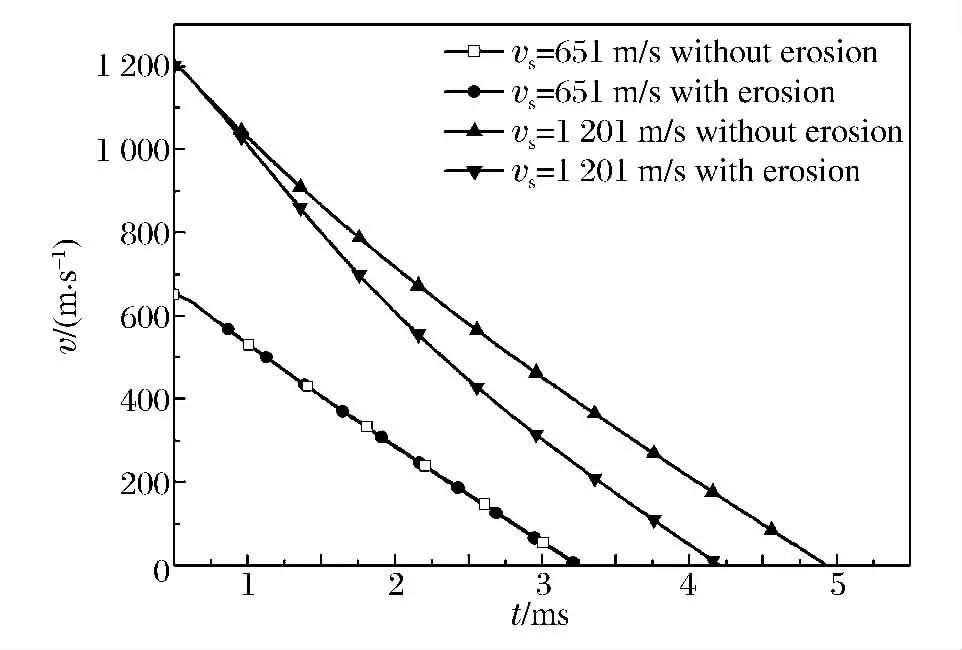
图6 （c）弹体侵彻过程中速度的时间历程曲线Fig.6 （c）Velocity of the projectiles versus time during penetration

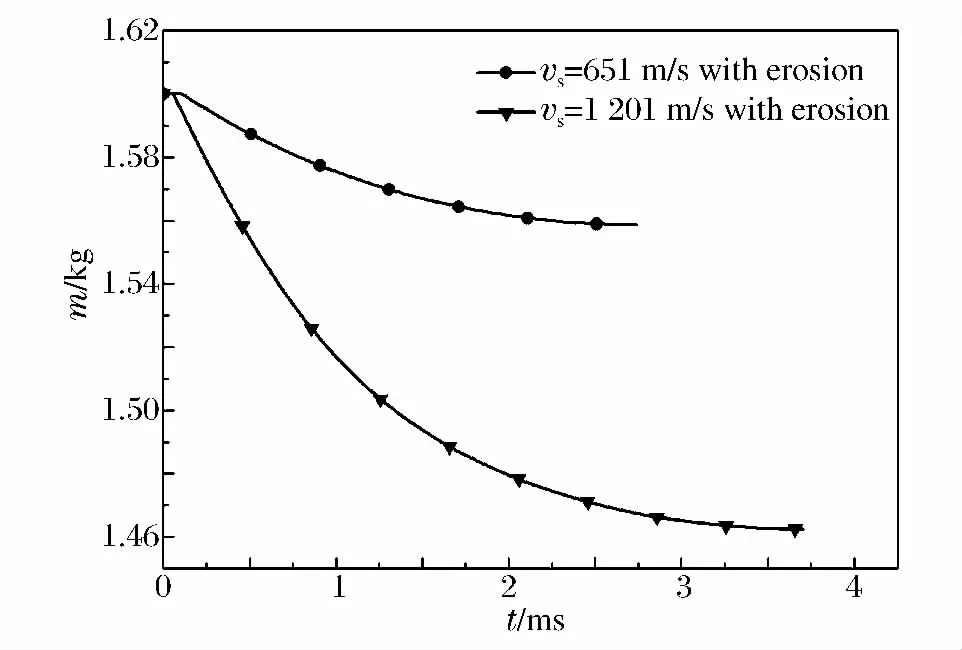
图6 （d）弹体侵彻过程中质量的时间历程曲线Fig.6 （d）Mass of the projectiles versus time during penetration

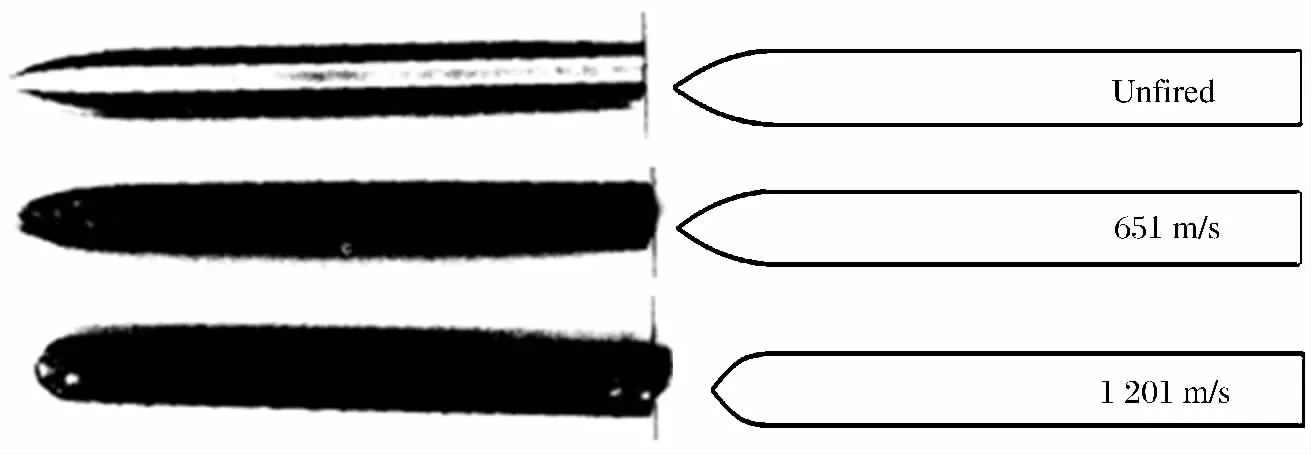
图7 回收弹体与侵蚀模型计算得到的弹体轮廓对比Fig.7 Residual projectiles by experiment and simulation

图8为弹体以1 201m／s的撞击速度侵彻时不同时刻的弹体轮廓，对应的时刻从左到右依次为 0、276.3、456.3、816.3、3 705.6μs，相应的瞬时速度依次为1 201.0、1 103.3、1 029.6、875.6、0m／s。高速条件 下，头部侵蚀较严重，且侵蚀现象在稳定侵彻的初期最剧烈，如图9所示，弹体质量损失率Δm／Δt峰值出 现 在0.06ms时 刻，而 由图6（a）知，弹体最大过载出现在0.6ms时刻，最大过载出现的时刻较质量损失率峰值出现的时刻有一定的滞后。相比之下，杆部的侵蚀可忽略。但是，随着侵彻的进行，头部与杆部的过渡段在不断回退。

图8 以1 201m／s的撞击速度侵彻时不同时刻的弹形Fig.8 Shape variation of the projectile with the initial impact velocity of 1 201m／s

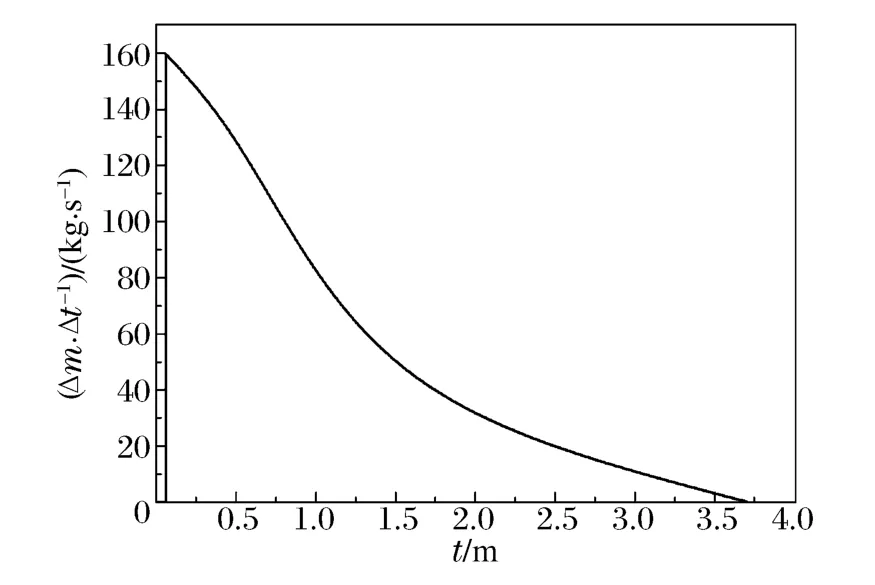
图9 以1 201m／s的撞击速度侵彻时，弹体质量损失率的时程曲线Fig.9 Mass loss rate versus time for the projectile with the initial impact velocity of 1 201m／s

弹体高速侵彻混凝土过程中，受到瞬时载荷作用，弹体处于高温、高压、高应变率的状态。由于侵彻时间短暂，弹体表面薄层的热量来不及扩散，当弹体材料表面微粒在高应变率下的温升对材料的软化大于应变硬化效应，出现塑性变形，宏观上表现为弹体侵蚀现象。图7为侵彻结束后回收的不同撞击速度下，弹体与侵蚀模型计算得到的弹体轮廓的对比，计算得到的弹体轮廓与实验后的弹体轮廓吻合较好。可以发现，随着撞击速度的增大，弹体发生了严重的侵蚀变形，其变形主要发生在弹体头部，弹体头部由卵形蜕变为钝头直至平头。由于理论假设的受力对称性，所以计算不会出现杆部弯曲等弹体动态结构响应现象。

侵彻过程中，弹体材料的屈服强度是影响侵彻效率的一个重要因素。这里取Yp分别为600、1 481和2 000MPa代入模型进行计算，撞击速度取1 069m／s，侵彻深度的计算结果分别为1.54、1.87、1.92m，对应的质量损失百分比分别为15.0%、7.0%、1.2%。弹体屈服强度的提高能较好地减少弹体的质量损失，提高弹体的侵彻深度。但是，由于质量侵蚀的存在，弹体初始头形被破坏，使得侵彻深度较理想刚性条件下都有下降。所以，在保证较小侵蚀的条件下，合理控制弹体头部的侵蚀分布，使弹体在侵彻过程中保持有利的头部外形，是提高弹体侵彻深度的一种重要方法。

5 结 论

基于模具与工件磨损中的Archard粘着磨损理论，采用从弹体微粒的细观塑性变形到宏观质量损失的分析方法，得到侵彻混凝土的弹体质量侵蚀表征模型，定义弹体表面的侵蚀速度，其大小与弹靶表面的法向应力和切向速度等因素有关，再运用动态球形空腔膨胀理论得到的弹体表面应力，计算得到了高速侵彻中弹体轮廓的钝化回退过程，该侵蚀模型能较好地计算弹体在高速条件下的侵彻深度和质量损失，与实验吻合较好。通过研究得出如下结论：（1）撞击速度是影响弹体质量损失最重要的因素，弹体侵蚀效应对侵彻时间和深度的影响随着撞击速度的增大而增强。（2）由于侵蚀效应作用，弹体侵彻中最大过载出现在开坑段结束后、稳定侵彻段的初始阶段，较质量损失率峰值有一定的滞后性，且最大过载较刚性条件下有较大提高。（3）提高弹体屈服强度能有效地减少弹体的质量损失，提高弹体的侵彻深度，在保证较小侵蚀的条件下，如何合理地控制弹体头部侵蚀分布，使得侵彻过程中弹体保持较好的头部外形，是提高侵彻深度的关键，也是下一步研究的重点。

［1］Forrestal M J，Frew D J，Hanchak S J，et al.Penetration of grout and concrete targets with ogive－nose steel projectiles［J］.International Journal of Impact Engineering，1996，18（5）：465－476.

［2］何翔，徐翔云，孙桂娟，等.弹体高速侵彻混凝土的效应实验［J］.爆炸与冲击，2010，30（1）：1－6.He Xiang，Xu Xiang－yun，Sun Gui－juan，et al.Experimental investigation on projectiles’high－velocity penetration into concrete targets［J］.Explosion and Shock Waves，2010，30（1）：1－6.

［3］杨建超，左新建，何翔，等.弹体高速侵彻混凝土质量侵蚀实验研究［J］.实验力学，2012，27（1）：122－127.Yang Jian－chao，Zuo Xin－jian，He Xiang，et al.Experimental study of projectile mass loss in high velocity penetration of concrete target［J］.Journal of Experimental Mechanics，2012，27（1）：122－127.

［4］Frew D J，Hanchak S J，Green M L，et al.Penetration of concrete targets with ogive－nose steel rods［J］.International Journal of Impact Engineering，1998，21（6）：489－497.

［5］Frew D J，Forrestal M J，Cargile J D.The effect of concrete target diameter on projectile deceleration and penetration depth［J］.International Journal of Impact Engineering，2006，32（10）：1584－1594.

［6］Silling S A，Forreatal M J.Mass loss from abrasion on ogival－nose steel projectile that penetrate concrete targets［J］.International Journal of Impact Engineering，2007，34（11）：1814－1820.

［7］陈小伟，杨世全，何丽灵.动能侵彻弹体的质量侵蚀模型分析［J］.力学学报，2009，41（3）：739－747.Chen Xiao－wei，Yang Shi－quan，He Li－ling.Modeling on mass abrasion of kinetic energy penetrator［J］.Chinese Journal of Theoretical and Applied Mechanics，2009，41（3）：739－747.

［8］Jones S E，Foster J C，Toness O A，et al.An estimate for mass loss from high velocity steel penetrators［C］∥Proceedings of the ASME PVP－435Conference on Thermal－Hydraulic Problems，Sloshing Phenomena，and Extreme Loads on Structures.New York：American Society of Mechanical Engineers，2002：227－237.

［9］Davis R N，Jones S E，Hughes M L.High－speed penetration of concrete using a new analytical model of velocitydependent friction［C］∥Proceedings of the ASME 2003Pressure Vessels and Piping Conference.New York：American Society of Mechanical Engineers，2003，454：111－116.

［10］Klepaczko J R，Hughes M L.Scaling of wear in kinetic penetrators［J］.International Journal of Impact Engineering，2005，31（4）：435－459.

［11］Guo L，He Y，Zhang X F，et al.Study mass loss at microscopic scale for a projectile penetration into concrete［J］.International Journal of Impact Engineering，2014，72（10）：17－25.

［12］何丽灵，陈小伟.高速侵彻混凝土弹体的形状演化模拟［J］.力学学报，2011，43（4）：707－715.He Li－ling，Chen Xiao－wei.Simulation of variation of projectile nose during high－speed penetration into concrete［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43（4）：707－715.

［13］He Li－ling，Chen Xiao－wei，He Xiang.Parametric study on mass loss of penetrators［J］.Acta Mechanica Sinica，2010，26：585－597.

［14］何丽灵.高速侵彻混凝土弹体的动力学行为研究：计及质量损失和头形钝化［D］.合肥：中国科学技术大学，2012：29－40.

［15］郑浩，何勇，郭磊，等.卵形弹丸高速正侵彻混凝土靶板的数值仿真［J］.系统仿真学报，2013，25（7）：1508－1512.Zheng Hao，He Yong，Guo Lei，et al.Numerical simulations of normal penetration of concrete target with ogivenose steel projectile by high－speed［J］.Journal of System Simulation，2013，25（7）：1508－1512.

［16］杨阳，何涛，文鹤鸣.弹体侵彻混凝土靶板过程中磨蚀问题的计算［J］.高压物理学报，2012，26（1）：83－88.Yang Yang，He Tao，Wen He－ming.An abrasion algorithm for ogive－nose steel projectile penetrating concrete target［J］.Chinese Journal of High Pressures Physics，2012，26（1）：83－88.

［17］Mu Zhong－cheng，Zhang Wei.An investigation on mass loss of ogival projectiles penetrating concrete targets［J］.International Journal of Impact Engineering，2011，38（8／9）：770－778.

［18］赵晓宁.高速弹体对混凝土侵彻效应研究［D］.南京：南京理工大学，2011：54－71.

［19］Archard J F.Contact and rubbing of flat surface［J］.Journal of Applied Physics，1953，24（8）：981－988.

［20］Archard J F.Friction between metal surfaces［J］.Wear，1986，113（1）：3－16.

［21］Burwell J T，Strang C D.On the empirical law of adhesive wear［J］.Journal of Applied Physics，1952，23（1）：18－28.

［22］Forrestal M J，Tzou D Y.A spherical cavity－expansion penetration model for concrete targets［J］.International Journal of Solids and Structures，1997，34（31／32）：4127－4146.