弹靶尺寸对陶瓷／金属复合装甲防护性能的影响＊

迟润强，Ahmad Serjouei ，范 峰，Idapalapati Sridhar

（1.哈尔滨工业大学土木工程学院，黑龙江 哈尔滨150001；2.School of Mechanical ＆ Aerospace Engineering，Nanyang Technological University，Singapore 639798）

陶瓷材料因具有高抗压强度、高硬度及低密度等突出优点而越来越广泛地被应用于装甲防弹领域。将陶瓷材料与塑性较好的金属材料复合在一起，可以更好地发挥2种材料各自的优点，提高防弹性能。获取陶瓷／金属复合装甲弹道极限速度是一个很重要的工程问题，数值模拟是解决此问题的有效手段。相对于实验方法，经过标定的数值模型不仅能够提供较为准确的弹道极限速度结果，还可以直观地分析侵彻过程，且耗费不大。目前，在对陶瓷／金属复合装甲撞击的数值模拟研究中，最普遍应用的是Lagrange模型，但其不能很好地处理单元大变形以及表征脆性材料的破碎问题。

为了解决上述问题，部分研究采用了SPH模型［1］，但SPH方法存在不稳定性，SPH粒子可能出现受拉失稳的问题［2］。因此，本文中采用将上述2种方法结合在一起的SPH－Lagrange模型，可以消除单一数值方法的局限性，提供更准确的模拟结果。利用Autodyn软件，建立经过实验标定的SPH－Lagrange数值模型进行数值计算，分析陶瓷／金属复合装甲弹道极限速度与弹靶尺寸的具体关系，并建立装甲弹道极限速度的经验公式。

1 数值模拟

选取文献［3］中的3个20mm脱壳穿甲弹（简称APDS子弹）撞击陶瓷／金属复合装甲实验作为验证数值模拟有效性的依据。复合装甲由99.5%氧化铝陶瓷前板及5083－H111铝合金后板组成，各次实验的前、后板厚度见表1，表中T1、T2分别表示前、后板的厚度，l为子弹剩余长度，v为子弹剩余速度。

表1 APDS子弹侵彻氧化铝陶瓷／铝合金复合装甲的实验与数值模拟结果［3］Table 1 Experimental and simulation results for APDS impacting bi－layer alumina／aluminum armor［3］

在所有实验中，APDS子弹以1 240m／s的速度垂直撞击复合装甲。20mm APDS子弹是一种次口径大威力子弹，由钨合金弹芯及轻质材料制作的风帽组成，直径12mm，长度61.5mm，质量72g［4］。在实验中，V.S.Gálvez［3］测量了APDS子弹穿透装甲之后的剩余长度和剩余速度，见表1。

利用Autodyn软件，采用二维轴对称模型，对上述实验工况进行数值模拟，有限元模型见图1。鉴于钨合金弹芯占20mm APDS子弹总质量的99%以上，仅建立了钨合金弹芯的有限元模型来代替APDS子弹，忽略了风帽对撞击效果的影响。APDS子弹与陶瓷前板为无网格的SPH模型，铝合金后板为有网格的Lagrange模型，前板的SPH粒子与后板有限元网格的边及节点在交界面上重合并利用Autodyn的“Join”功能固连在一起。装甲前、后板径向边界处均设置轴向与径向固定约束。

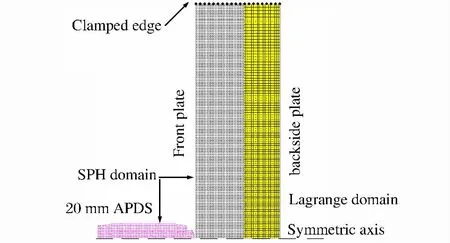
图1 二维轴对称数值模型Fig.1 Two－dimensional axisymmetric numerical model

采用SPH方法对子弹和陶瓷前板建模的主要原因［5］如下：如果APDS子弹与陶瓷前板是Lagrange模型，当弹靶接触区域内的单元在撞击过程中变形增大到一定程度，Autodyn软件通常会采用删除这些单元的方式（即侵蚀算法）来保证计算能够持续进行，此时陶瓷材料前部的压力会因单元消失而在短时间内突然消失，从而直接影响相邻位置陶瓷单元内的压力状态，而陶瓷材料在力作用下的响应受到施加在自身上的压力的影响很大，因此这会造成陶瓷材料强度降低；在SPH模型中，SPH粒子并不会因为材料大变形而被删除，陶瓷前部的压力会一直保持并连续变化，陶瓷材料的强度不会瞬间降低，能够保证计算结果的准确性。另外，陶瓷为脆性材料，在撞击下必然发生破碎；因为没有网格的限制，SPH模型能够更好的表现陶瓷破碎之后的运动。

鉴于5083－H111铝合金的材料参数较难从文献中获取，在本文中采用5083－H116铝合金的参数代替。5083－H116铝合金与钨合金材料均采用Johnson－cook本构模型［6］与失效模型［7］描述，具体参数参见文献［8－9］。其中，5083－H116铝合金JC失效模型中的参数d4未采用文献［8］供的数值，这是因为文献中采用的是一种修正的JC失效模型，其表达式与Autodyn材料库中的原始JC失效模型不同。本文中根据该文献所提供的实验数据点，基于原始JC失效模型表达式，采用曲线拟合方法确定该参数值。氧化铝陶瓷采用JH－2材料模型［10］，该模型被广泛用于描述脆性材料在高压、高应变率和大变形条件下的力学响应，包括3个部分：强度模型、损伤模型和状态方程，99.5%氧化铝材料所采用的JH－2模型参数参见文献［11－12］。

图2给出了APDS子弹侵彻装甲的数值模拟过程。

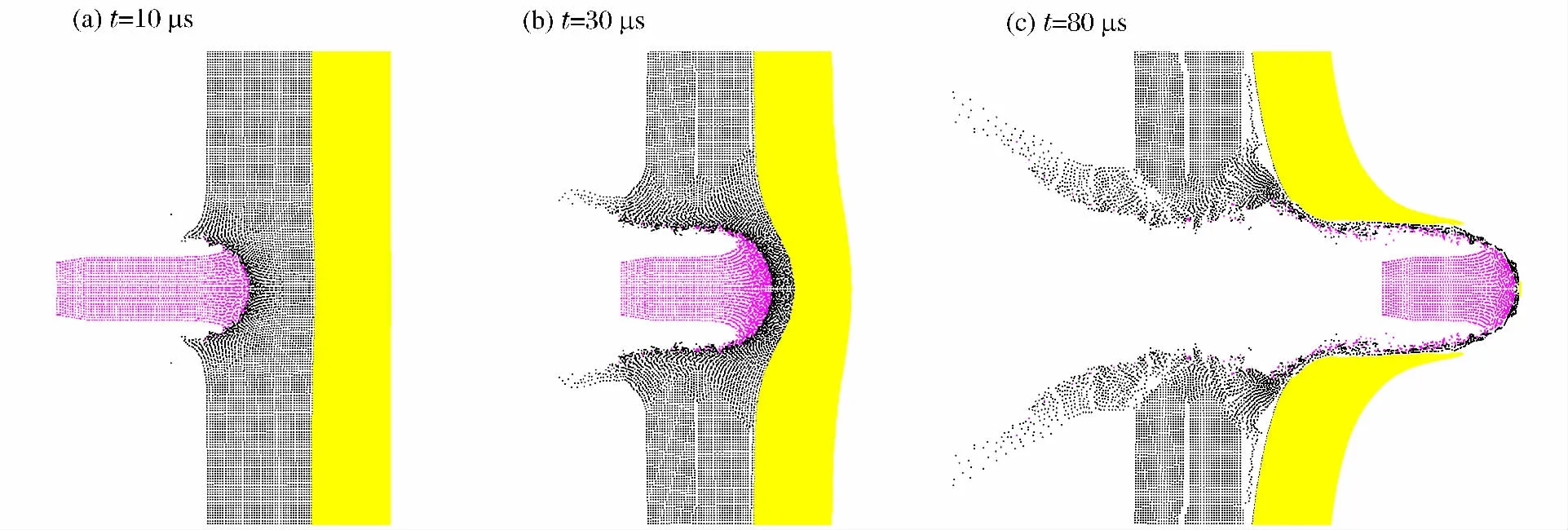
图2 APDS子弹侵彻氧化铝陶瓷／铝合金复合装甲的过程Fig.2 The process of APDS impacting alumina／aluminum armor

由图2可见，前板中破碎的陶瓷材料和子弹前部被侵蚀掉的钨合金材料可以自由运动，模拟结果更接近实际的物理现象，证明SPH方法模拟大变形和破碎行为的有效性。此外，数值模拟还给出了AP－DS子弹在穿透装甲后的剩余速度与剩余长度，如表1所示。比较可见，数值模拟结果与实验结果符合较好，说明本文中的有限元模型能够有效模拟包含上述3种材料的子弹侵彻陶瓷／金属复合装甲问题。

2 弹靶尺寸对装甲弹道极限速度的影响

利用上述有限元建模方法与材料参数，改变弹靶尺寸，进行一系列数值计算。考虑到APDS子弹弹芯的几何形状比较复杂，采用具有代表性的圆柱体子弹，便于对其形状进行几何描述。弹靶尺寸参数包括：子弹直径d与长度L、圆形前板厚度T1与直径D1、圆形后板厚度T2与直径D2。通过改变数值模拟中的撞击速度，采用逐渐逼近的方法，获得了在不同弹靶尺寸组合下装甲的弹道极限速度vL。

对子弹穿甲过程进行量纲分析，并通过数值模拟发现：当弹靶材料不变而尺寸变化时所有材料参数对装甲弹道极限速度无影响。因此，装甲弹道极限速度vL可表示为：

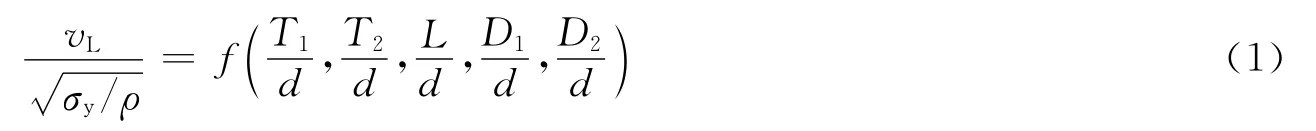
式中：σy与ρ分别为子弹材料的屈服强度与密度。

进一步，将vL的表达式写为：

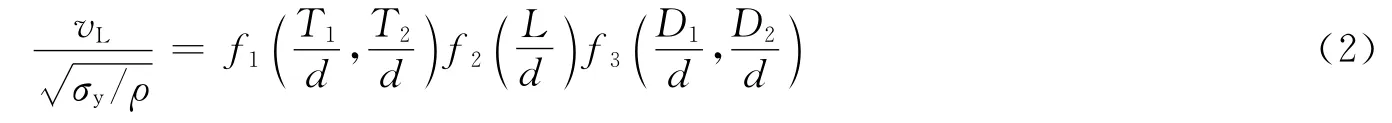
式中：f1、f2和f3为3个子函数，分别表述各尺寸参数与装甲弹道极限速度的关系。

基于数值模拟结果，分别分析T1／d、T2／d、L／d、D1／d与D2／d对vL的影响规律并确定上述各子函数的形式。当考虑某一个参数的影响时，其他参数均保持不变，子弹直径d均为12mm。

2.1 T1／d与T2／d对装甲弹道极限速度的影响

函数f1同时考虑了T1／d与T2／d对弹道极限速度的影响。对此共进行了4组数值模拟，采用控制变量法 ，分别考虑T1／d与T2／d对复合装甲弹道极限速度的影响，如图3～4所示，以及对单层靶板弹道极限速度的影响，如图5～6所示。

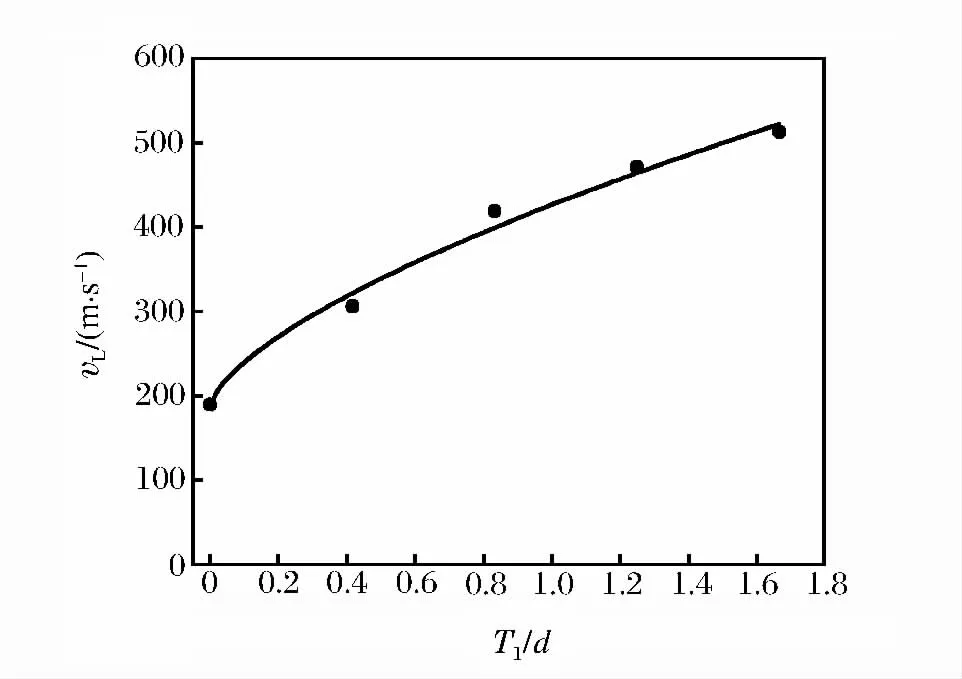
图3 复合装甲弹道极限速度随T1／d比值变化关系Fig.3 Variation of ballistic limit velocity in composite armor with the ratio of T1／d

图4 复合装甲弹道极限速度随T2／d比值变化关系Fig.4 Variation of ballistic limit velocity in composite armor with the ratio of T2／d

图3～6中对应的靶板的几何参数为L／d＝3，D1／d＝D2／d＝16.67。图3中设T2／d＝0.83，图4中设T1／d＝1.25；图5～6中，由于只考虑单层靶板，因此对应的条件T1／d＝0和T2／d＝0。由图中可知，vL随T1／d与T2／d的增加而增加，且可认为其与二者近似呈幂函数关系。另外，相同厚度的单层铝合金板比单层氧化铝陶瓷板具有更高的弹道极限速度。

综合以上分析，提出子函数f1的表达式如下：

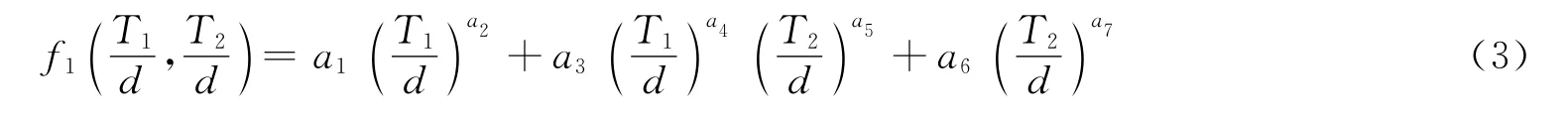
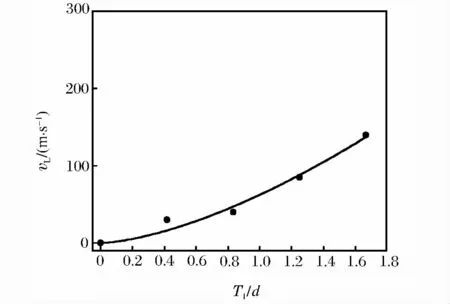
图5 单层装甲弹道极限速度随T1／d比值变化关系Fig.5 Variation of ballistic limit velocity in single plate with the ratio of T1／d

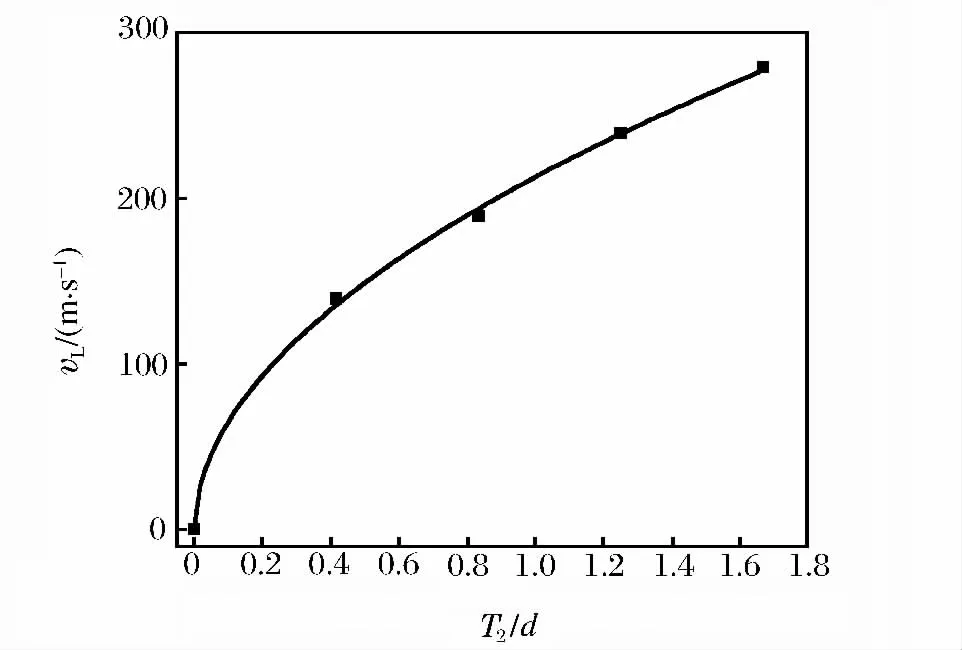
图6 单层装甲弹道极限速度随T2／d比值变化关系Fig.6 Variation of ballistic limit velocity in single plate with the ratio of T2／d

式中：a1～a7为待定系数。

2.2 L／d对装甲弹道极限速度的影响

对5个具有不同L／d值的子弹撞击装甲的工况进行了数值模拟，图7给出了弹道极限速度vL与L／d的关系，图7中对应的复合靶板的几何参数为T1／d＝T2／d＝0.83，D1／d＝D2／d＝16.67。由图中可知，vL随L／d的增加而降低，将其用幂函数表示如下：

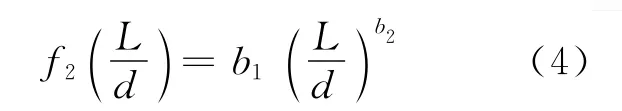
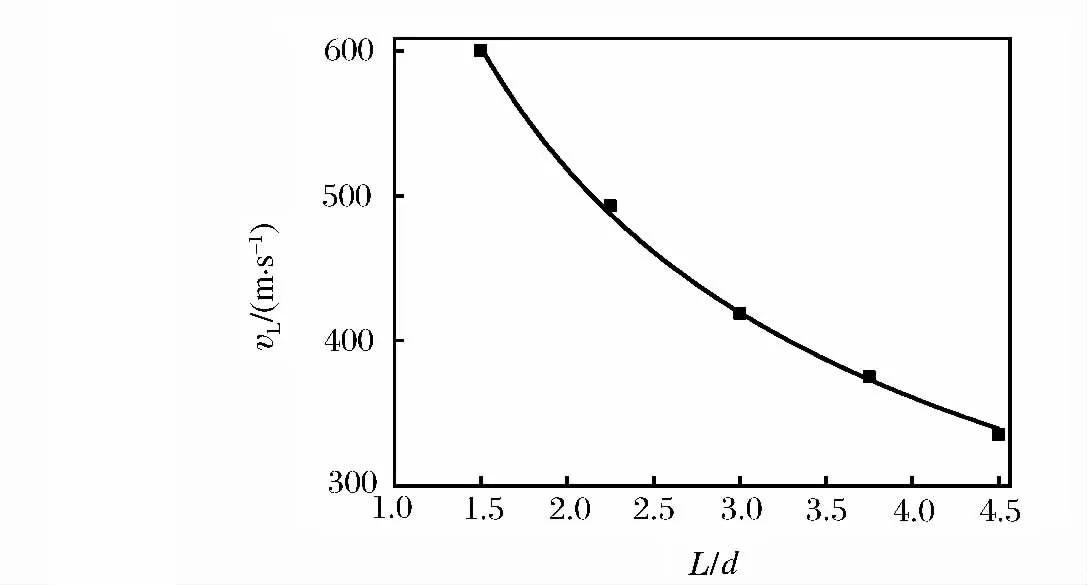
图7 复合装甲弹道极限速度随L／d比值变化关系Fig.7 Variation of ballistic limit velocity in composite armor with the ratio of L／d

式中：b1、b2为待定系数。

2.3 D1／d与D2／d对装甲弹道极限速度的影响

由于陶瓷前板与金属后板材料特性相差很大，二者的平面尺寸对装甲弹道极限速度的影响规律必然有较大差异。考虑到装甲前、后板的平面尺寸在实际情形中不可能小于子弹直径，在模拟中，D1／d与D2／d均大于1。

陶瓷是一种脆性材料，受力所产生的塑性变形很小，在子弹撞击下，陶瓷前板的破碎主要发生在撞击点附近的锥形区域内，该区域以外的陶瓷材料基本不参与子弹对装甲后板的侵彻过程。因此，可认为当陶瓷板平面尺寸在小于陶瓷锥尺寸的范围内变化时才对装甲弹道极限速度产生影响。

为了验证此观点的正确性，对不同D1／d值工况下的复合装甲进行了撞击模拟，图8给出了装甲弹道极限速度与D1／d的关系。图8中对应的复合靶板的几何参数为L／d＝3，T1／d＝T2／d＝0.83，D2／d＝16.67。

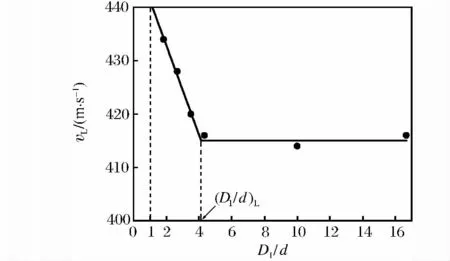
图8 复合装甲弹道极限速度随D1／d比值变化关系Fig.8 Variation of ballistic limit velocity in composite armor with the ratio of D1／d

由图8可见，弹道极限速度vL随D1／d的增加并非单调变化。存在一个临界值当时，vL随D1／d的增加而线性减小，当时，vL保持不变。对图8中的计算值进行分段曲线拟合，获得了D1／d在有效范围内所对应的vL值，确定2条曲线分界点当 D1／d＝1时，对应vL的最大值；当时，对应vL的最小值。若以弹道极限速度的最小值为标准，2个极值之差与其相比不超过6%，这说明D1／d的变化对装甲弹道极限速度的影响不明显。

图9给出了复合装甲中陶瓷前板在子弹侵彻过程中形成的锥形陶瓷破碎区形态。根据计算得到陶瓷前板临界平面尺寸也被标注在图中，比较发现几乎与陶瓷破碎锥最大直径相同。综上说明：对于仅陶瓷前板平面尺寸不同而其他弹靶参数均相同的撞击，必然存在一个临界前板平面尺寸，该尺寸即为陶瓷破碎锥直径最大值；仅当陶瓷前板平面尺寸小于该临界值时，其变化才对装甲弹道极限速度产生影响。

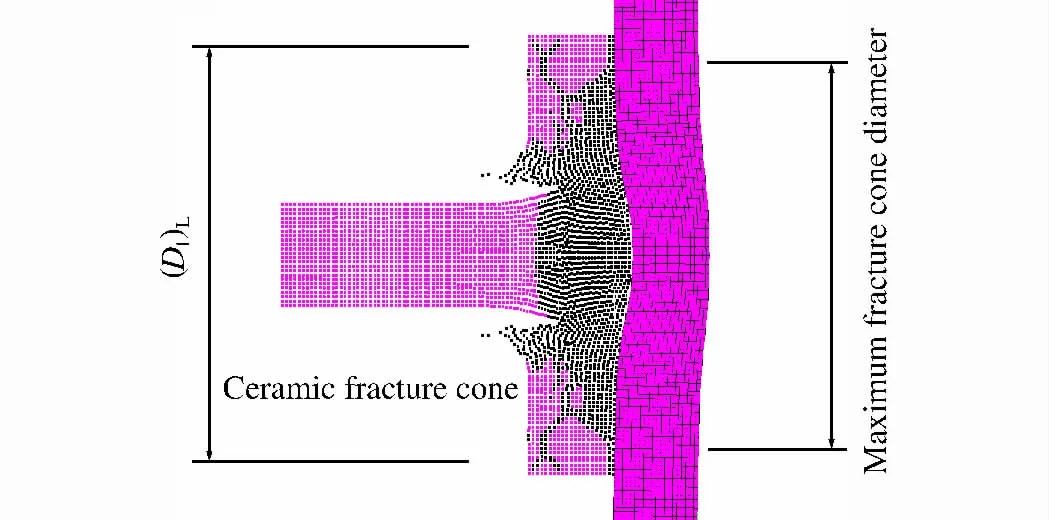
图9 弹体撞击过程中陶瓷破碎锥的最大直径Fig.9 Ceramic maximum fracture cone diameter in process of impacting

为了解释vL随D1／d（1＜D1／d＜ （D1／d）L）增加而减小的现象，对2个不同组合的装甲开展相同速度撞击的数值模拟，如图10所示，除陶瓷前板平面尺寸外，其余弹靶参数均相同。

图10 具有不同D1／d值的装甲被撞击时的形态比较Fig.10 Impacting mode comparison for two armors with different D1／d

装甲Ⅰ和装甲Ⅱ的D1／d值分别取1.83和10，二者位于的两侧，且差别较大，这样可以更清晰地看出其对撞击过程影响的区别。图10给出了不同组合的装甲在子弹撞击过程中2个时刻的形态，图形上半部分对应装甲Ⅰ，下半部分对应装甲Ⅱ。在33μs时刻，2种装甲中铝合金后板的变形明显不同，相比于装甲Ⅱ，装甲Ⅰ中后板的变形更集中于中间部分，这使其能够更有效地限制破碎的陶瓷材料沿径向扩散，直到撞击过程后期129μs时刻，子弹与后板之间仍保存有更多的陶瓷材料，从而增大子弹与陶瓷材料在后板上的作用面积，使其后板更难被穿透。因此，装甲Ⅰ的弹道极限速度相对于装甲Ⅱ的更高。

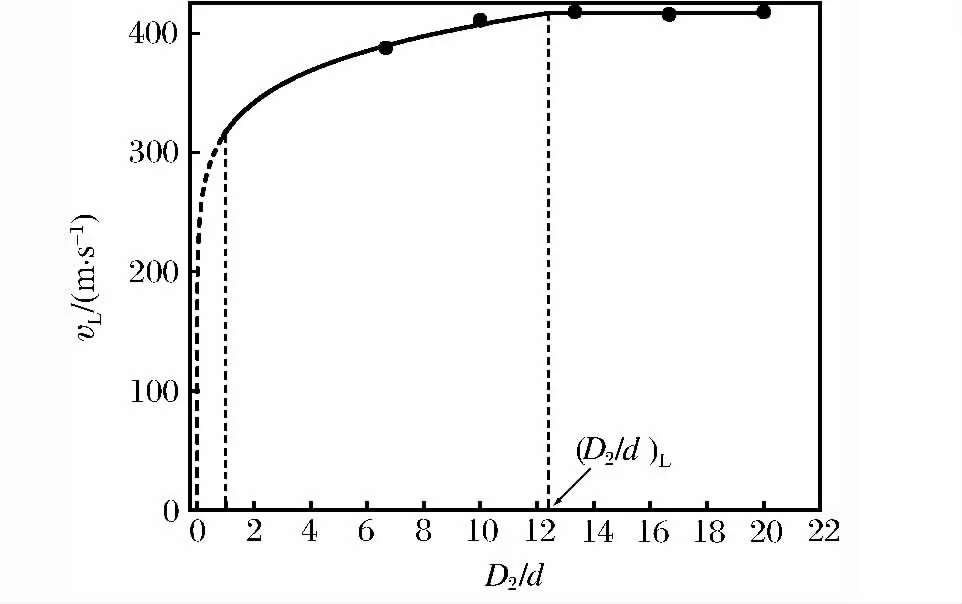
图11 复合装甲弹道极限速度随D2／d比值变化关系Fig.11 Variation of ballistic limit velocity in composite armor with the ratio of D2／d

复合装甲后板为铝合金材料，具有较好的塑性，可以预测，在冲击下其塑性变形应该存在于一个较大的平面范围内。对具有不同D2／d值的复合装甲进行撞击的数值模拟，弹道极限速度vL与D2／d的关系如图11所示。图11中对应的复合靶板的几何参数为L／d＝3，T1／d＝T2／d＝0.83。复合装甲的D1／d值与D2／d保持相同，并且大于 （D1／d）L，以消除前者对弹道极限速度的影响。

对图11中的数据进行分段曲线拟合，获得2条曲线，二者分界点设为当时，vL随D2／d的增加而增加；当时，vL为定值。若以图11中弹道极限速度最大值为标准，2个极值之差与其之比为24.5%。此外，明显大于这些都说明D2／d对于弹道极限速度的影响大于D1／d的影响。

根据图8和图11中所示装甲弹道极限速度与D1／d及D2／d的关系，并考虑D1／d不能大于D2／d，且在范围内，提出子函数f3的形式如下：

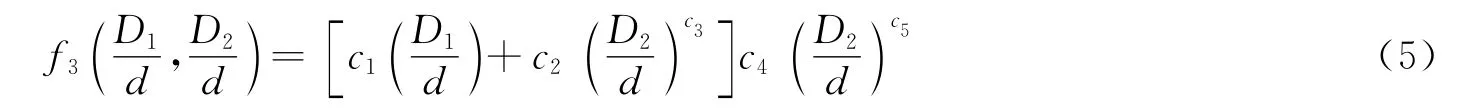
式中：c1～c5为待定系数。从量纲的角度看，分界点应随L／d、T1／d和T2／d的变化而变化，但该问题非本文研究重点，暂未开展工作。

2.4 装甲弹道极限速度的经验方程

将前文中已获得的3个子函数表达式带入式（2），即可得到复合装甲弹道极限速度表达式。基于该式，利用数值模拟结果，采用最小二乘法进行回归分析，便可获得各待定系数的值。考虑到通常情况下装甲前后板的平面尺寸往往比子弹直径大的多，在模拟中忽略了子弹直径对弹道极限速度的影响，取D1／d＝D2／d＝20。最后获得氧化铝陶瓷（99.5%）／铝合金（Al 5083－H116）复合装甲在钨合金子弹撞击下的弹道极限速度与弹靶几何参数L／d、T1／d和T2／d之间关系的经验公式如下：

尽管式（6）仅适用于本文中所涉及的弹靶材料，但可预见的是，其方程形式以及各几何参数对陶瓷／金属复合装甲的影响规律可以推广到更多材料。

3 结 论

利用数值模拟手段对氧化铝陶瓷／铝合金复合装甲在钨合金子弹撞击下的弹道极限速度与弹靶尺寸之间的关系进行了分析。研究发现：装甲弹道极限速度随T1／d和T2／d的增加而增大，随L／d的增加而减小；D1／d与D2／d只在一定范围内影响装甲弹道极限速度，当二者超过其临界值后，对弹道极限速度无影响；在影响范围内，装甲弹道极限速度随D1／d的增加而线性减小，随D2／d的增加而增大。此外还分析了D1／d影响装甲弹道极限速度的机理。建立一个装甲弹道极限速度的经验公式，其形式可作为其他陶瓷／金属复合装甲弹道极限速度的研究提供参考。

［1］张伟，胡德安，韩旭，等.陶瓷／金属复合装甲冲击响应的三维SPH 法分析［J］.爆炸与冲击，2011，31（4）：373－379.Zhang Wei，Hu De－an，Han Xu，et al.Three－dimensional SPH analysis of impact responses of ceramic／metal composite armors［J］.Explosion and Shock Waves，2011，31（4）：373－379.

［2］Swegle J W，Hicks D L，Attaway S W.Smoothed particle hydrodynamics stability analysis［J］.Journal of Computational Physics，1995，116（1）：123－134.

［3］Gálvez V S，Paradela L S.Analysis of failure of add－on armour for vehicle protection against ballistic impact［J］.Engineering Failure Analysis，2009，16（6）：1837－1845.

［4］Abrate S.Impact engineering of composite structures［M］.New York：Springer，2011.

［5］Johnson G R，Stryk R A，Beissel S R，et al.An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation［J］.International Journal of Impact Engineering，2002，27（10）：997－1013.

［6］Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］∥Proceedings of the Seventh International Symposium on Ballistics.Netherlands，1983：541－547.

［7］Johnson G R，Cook W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechnics，1985，21（1）：31－48.

［8］Clausen A H，Borvik T，Hopperstad O S，et al.Flow and fracture characteristics of aluminium alloy AA5083－H116as function of strain rate，temperature and triaxiality［J］.Materials Science and Engineering：A，2004，364（1／2）：260－272.

［9］Lee J K.Analysis of multi－layered materials under high velocity impact using CTH［D］.Ohio：Air Force Institute of Technology，2008.

［10］Johnson G R，Holmquist T J.An improved computational constitutive model for brittle materials［J］.AIP Conference Proceedings，1994，309（1）：981－984.

［11］Anderson C E，Johnson G R，Holmquist T J.Ballistic experiments and computations of confined 99.5%AL2O3 ceramic tiles［C］∥Proceeding of Fifteenth International Symposium on Ballistics.Jerusalem，Israel，1995.

［12］Lundberg P，Westerling L，Lundberg B.Influence of scale on the penetration of tungsten rods into steel－backed alumina targets［J］.International Journal of Impact Engineering，1996，18（4）：403－416.