谈塔式太阳能热发电系统的数学公式

何开浩

(宁波市中医院,浙江宁波 315010)

谈塔式太阳能热发电系统的数学公式

何开浩

(宁波市中医院,浙江宁波 315010)

我们现在使用的能源还是以石油、煤炭、天然气为主。这些化石性能源不仅数量有限，总有消耗殆尽的一天，而且大量使用还会造成严重的环境污染。使用大阳能是最好的能源利用方式，因为太阳的能源是取之不尽、用之不竭的。但是于由于现在太阳能发电的成本太高，效率太低，很难实现商业化价值开发，所以难以普及。有一种叫“塔式太阳能热发电技术”是成本很低、太阳能利用效率也很高的技术。但是，由于定日镜聚光瞄准技术一直没有解决，使得这么好的塔式太阳能热利用技术到到现在还停留在科学研究阶段，这一技术问世30多年来一直没有很好利用而造福人类。

为了解决这一问题，我发明一种叫做“塔式太阳能热发电系统的聚光瞄准装置”技术，其原理非常简单，看了下面的原理图和介绍，谁都会明白：(见图1)

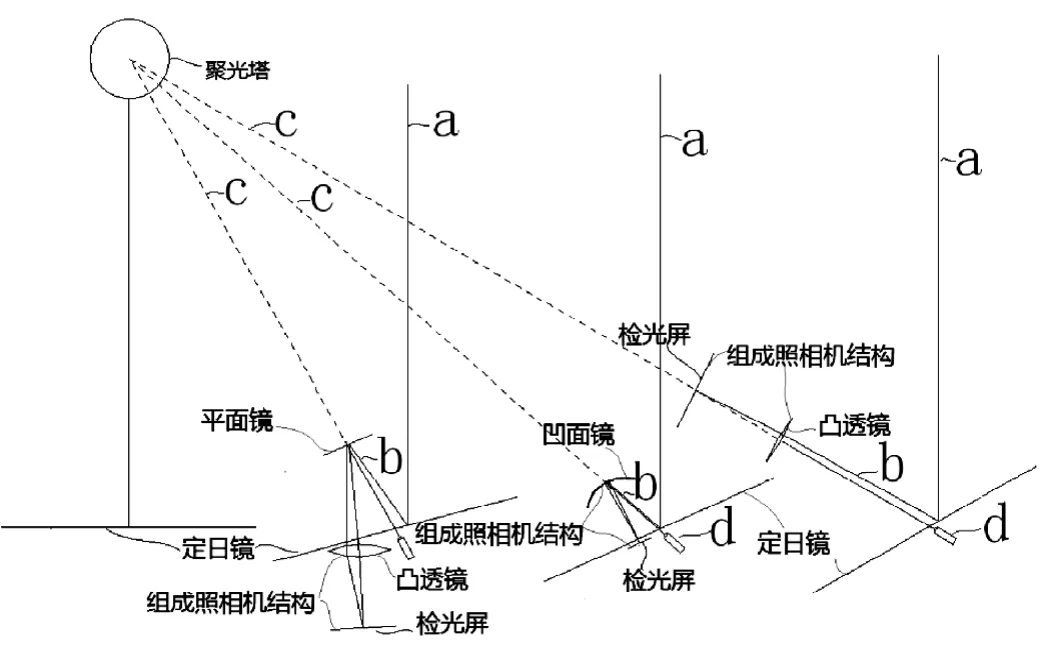
图1 《塔式太阳能热发电系统的聚光瞄准装置》原理图（有多种实施方式）

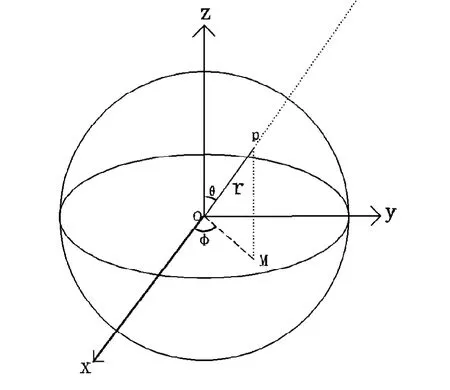
图2

这一专利的实施方法特别简单，利用平行光线通过凹面镜反射或者凸透镜折射会在焦点处聚集成一点，以这一原理来判断太阳和激光束是否并行。从而判断太阳光是否被正确的反射到目标上去。虽然太阳光不是绝对的平行光线，所在焦点处聚集成的只是个圆斑而不是一点，而激光束能聚焦成一点。但是我们可以检测激光束聚焦成的这一点是否在太阳光聚集成的圆斑中点就行。

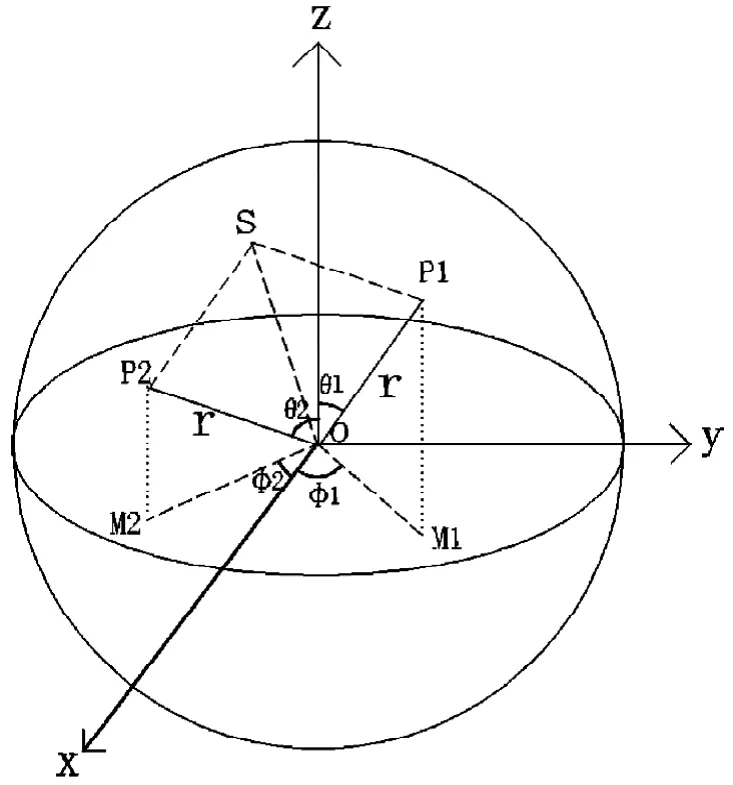
图3

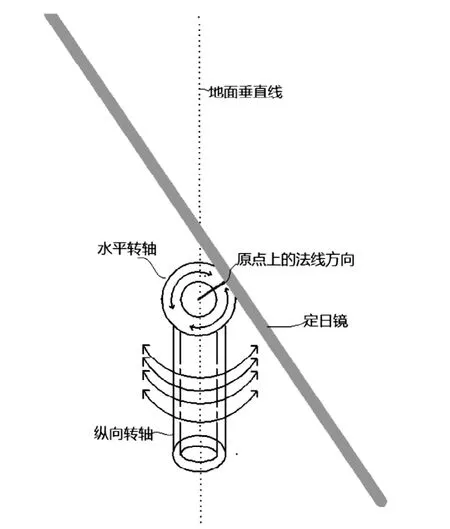
图4

这种检测完全可以用现在很普及的数码相机或者聊天摄像头来完成，数码相机或者聊天摄像头里面都有芯片，只要稍微对其进行重新编程用来分析激光束聚焦成的这一点是否在太阳光聚集成的圆斑中点。如果检测到检测激光束聚焦成的这一点偏离太阳光聚集成的圆斑中点，那么芯片就可以根据偏离的方向和程度来控制安装在定日镜里的步进电机运行，从而对定日镜作相应调整。这时候检光屏上太阳光聚集成的圆斑也会相应的运动，直到激光束聚焦成的这一点不偏离太阳光聚集成的圆斑中点，芯片控制安装在定日镜里的步进电机停止运行。这种程序只是一个非常简单的小程序，要实现根本没有什么困难。

我把我的发明资料寄给中国科学院，向一位德高望重的老院士请教。老院士给我提出了一个实际问题，他说：“阴天或阳光不好，如何跟踪，不跟踪会出现对环境的光污染。”

图5

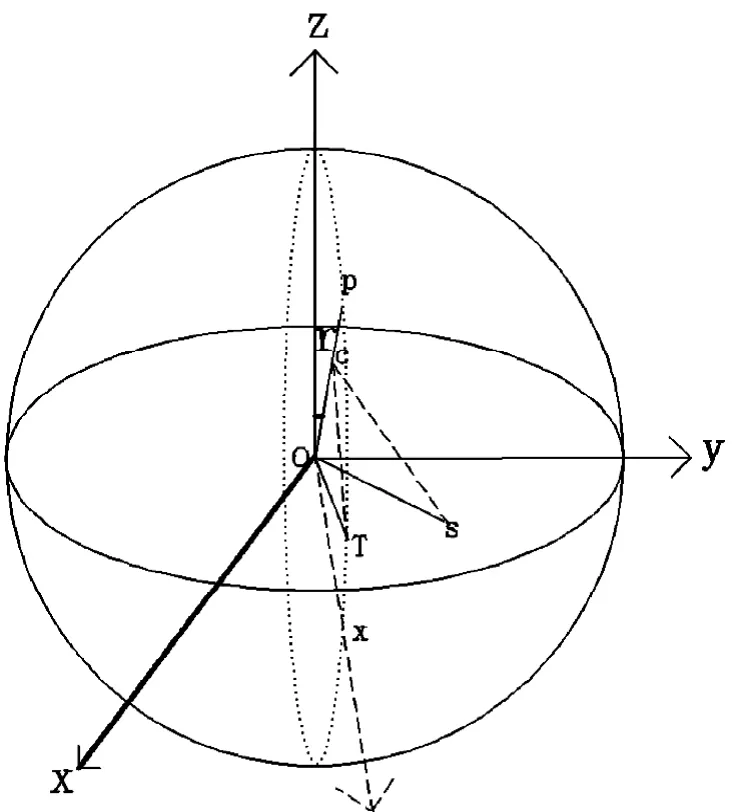
图6

要解决这个问题就必须让发电系统做到在人看不见太阳的时候，通过我们计算太阳位置，照样能够非常准确的运行。经过认真思考，我终于找到了一些关于这方面的数学计算公式。下面我慢慢介绍：

要计算定日镜方向，那就要给定日镜人建立一个三维坐标系，我们设这个坐标以定日镜的活动中心为原点。X轴向正南方，Y轴向正东方，Z轴向正上方。要计算太阳光线和其他直线的方向，还必须用这个三维坐标系中的球坐标来确定每个定日镜的方向。

图2就是一个球坐标。

球坐标通俗讲就是我假设有一个以坐标原点O为球心，半径为r的球罩在那里。假设有一条连线从太阳中心到原点O，这连线必然要经过假设的球的表面，我们把连线与球表面的交点标记为P点。这样我们就可以用直线OP来表示光线从哪个方向射来的，并且用点P的各项数值计算这条光线。在球坐标中，这个P点是用这三个有次序的数(r，θ，φ)来确定，其中r为原点O与点P间的距离(也就是球半径)；θ为有向线段OP与z轴正向的夹角，我们称其为“仰角”；图中M为点P在XOY面上的投影；φ为X轴正向与投影线OM的夹角，我们称其为“方位角”。

有了这三个数值，我们就可以计算出p点在直角坐标系中的坐标值(x，y，z)了。公式是这样 x=r·sinθ·cosφ， y= r·sinθ·sin φ， z= r·cosφ

反过来，如果我知道某一点的坐标值也可计算出球坐标的三个值。公式是这样的：

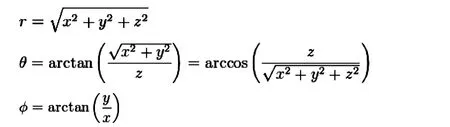
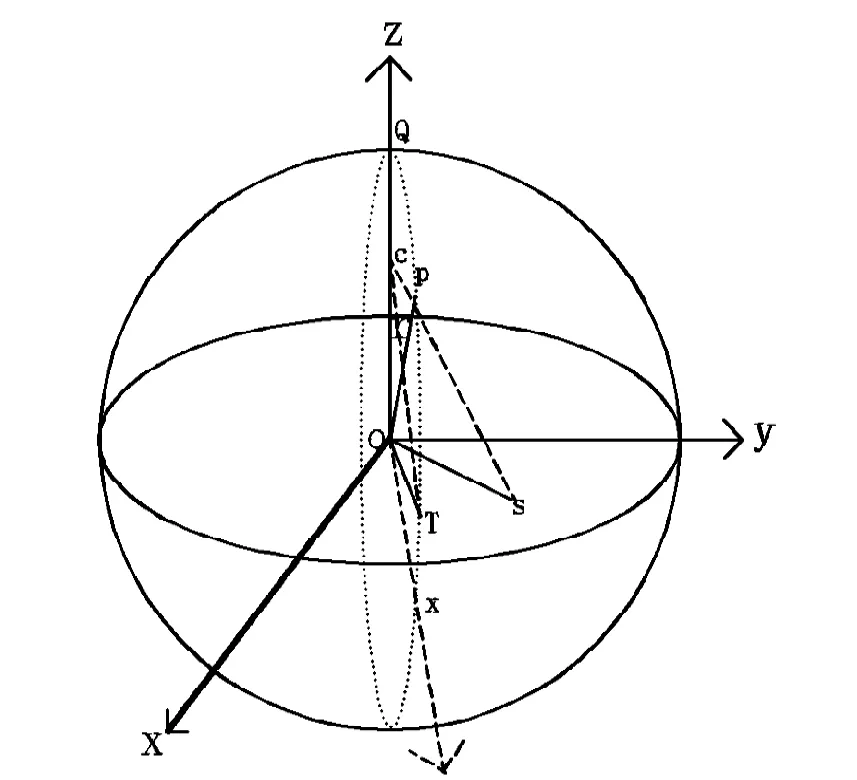
图6

球坐标明白了，接下来就要计算了。我们假设把太阳中心和坐标原点连一条连线(也就是太阳光照射到原点的光线)，这条连线同样会经过球坐标表面，我们把连线与球坐标表面的交点设为P1，其方位角、仰角和半径分別为(φ1，θ1，r)。同样的我们假设把坐标原点和光线要反射到的目标点连一条连线，这条连线同样会经过球坐标表面，我们把连线与球坐标表面的交点设为P2，其方位角、仰角和半径分別 为(φ2，θ2，r)。如图3。

光线反射的规律是入射角等于反射角；入射角是入射光线与法线形成的夹角；反射角是反射光线与法线形成的夹角；法线是定日镜平面的垂直线。要把从P1O线射来的光线沿着OP2这条线反射出去，法线就应该是∠P1OP2的角平分线。角平分线通常可以用向量相加的方法，用菱形对角线来确定。就是或者，因为向量和向量起点都是原点O(0，0，0)，所以计算结果就很简单，二个向量相加后的向量终点的坐标值为S(x1+x1，y1+y2，z1+z2)，就是图中S点。因为上OP1、OP2长度相等，都是球的半径r，起点为同一点原点O(0，0，0)。根据平行四边形定则，可以证明，四边形OP1SP2为菱形。那么OS是菱形OP1SP2对的对角线了，所以OS就是∠P1OP2的角平分线、就是我们要找的定日镜在原点O上的法线。根据直角坐标与球坐标换算公式，我们可以得出定日镜上法线的方位角、仰角计算公式分别为：

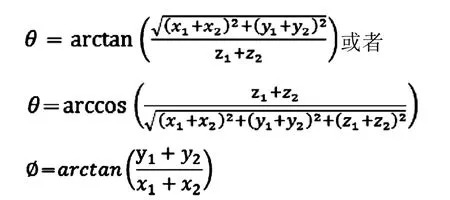
P1点坐标(x1，y1，z1)，P2点坐标(x2，y2，z2)都包含有一个不确定的值：球坐标半径r，那怎么办呢？这不要紧，这个值无论设置成大于零的什么数都没有关系，因为填入公式后，这个r值刚好会在分子分母中互相抵消。

有了这个计算公式，就可以用这个公式计算出的数值去定位定日镜的方位角和仰角。定位具体方法，可以用下这图4这装置来实施。

这种装置由纵向转轴和水平转轴二个转轴组成，定日镜就安装在水平转轴上。纵向转轴的铀线方向与地面垂直，可以作水平方向转动，转动时可以改变定日镜的方位角。水平转轴的轴线方向是水平的，转动时可以让定日镜上下翻转，这样翻转就可以改变定日镜的仰角。

有了这个数学公式和定位装置，我们即使看不到太阳，只要知道太阳这个时候应在什么位置，定日镜就能准确运行。那我们怎么知道太阳这个时候应该在什么位置呢？

一般情况下是我们可以通过天文数据知道。这个时候，太阳应该在赤道附近，多少经度， 多少纬度的那个地方的正上方。对于这种经纬度数据，我们还应该转换一下，将其转换成在这个时候太阳相对于定日镜的仰角和方位角。

实际上地球的经纬度就是球坐标的一种变形，地球南北极就是坐标的Z轴。我们可以把南极到北极方向的地球极线，设成Z轴方向。那赤道面就是坐标的XOY面。在赤道面上，从西经90度到东经90度的直线方向，设为坐标的X轴方向。赤道面上从经度0度到经度180度的直线方向，设为坐标的 Y轴方向。这样经纬度数值转化成方位角和仰角非常方便。东经的方位角是东经经度减去90度，西经的方位角是270度减去西经经度。北纬的仰角就是90度减去北纬纬度，南纬的仰角就是90度加上南纬纬度。

但是，我们定日镜的坐标是以当地的地面垂直线正上方为Z轴方向；当地的水平面上，正南方向为X轴方向；正东方向为Y轴方向。二个坐标系的方向都不一致，所以，这二坐标系的坐标值必须要互相转换。

在这里，我们要先说一说球坐标的一个特性。假如，球坐标上有一个点P，其仰角为θ，距离为球半经r。而其方位角是变化的，从0度开始慢慢增加，那么P点的位置也要随之慢慢变化，当方位角一直增加到360度后。P点位置变化的轨迹就是一个完整的圆。我们把这个圆叫做“同仰角圆”。如图5。

这个同仰角圆与直角坐标系与XOY平面平行，圆的半径是r·sinθ，圆心是在Z轴上，离球心O点距离为r·cosθ的C点上。假设Z轴与球面的交点为Q，坐标为(Xq，yq，zq)，那么同仰角圆的圆心C点的坐标就是(cosθ·xq，cosθ·yq，cosθ·zq)。

搞清同仰角圆这些性质，我们就可以在已知点P仰角和坐标值的情况下，计算出P点的方位角了。方法是在P点的同仰角圆上，找出一个已知方位角的点P1，连接P1C、PC。那么P点的方位角就是P1点的方位角再加上角∠PCP1。我们就是用这种原理，来计算S点相对于定日镜球坐标的方位角的。下面是具体的计算过程：

假如我们在东经n度，北纬m度的某一个地方P点，有一塔式太阳能电站，建了许多定日镜。某一天为阴天，当地观察不到太阳的位置。但是通过天文数据知道，这个时候太阳应该赤道附近，东经N度，北纬M度S点的正上方。我们怎样计算出，对于P点的定日镜来说，这个时候太阳的仰角和方位角应该是多少呢？

P处的定日镜Z轴方向为垂直向上，就是说定日镜Z轴与地球球心O点与P点连线一致。所以可以用直线OP来代表定日镜Z轴。太阳位置在S点处的正上方，说明S点在太阳中心与地球球心O点的连线上。所以可以用直线SO来标注太阳光的方向。如图6。

P点和S点经纬度数值，可以通过简单的加减非常容易换算成球坐标的方位角和仰角，换算 后各自分别记为：P(φp，θp)，S(φs，θs)。根据直角坐标与球坐标换算公式，可以计算出各自的坐标分别为：P

(xP，xP，ZP)，S(xS，xS，xS)。可以看到P点处太阳的仰角应该是OS与OP的夹角∠SOP

仰角计算相对简单，接下来要计算方位角了。要计算方位角，首先要知道定日镜坐标的X轴或XOZ面在哪里。我们知道定日镜的X轴的方向是当地位置P点处水平面上的正南方。那么X轴的向反方向是指向北极的。这么一来Z轴与OP组成平面，应该与定日镜坐标的XOZ面重合，也就是说地球过P的经纬度的那一条经度线就在定日镜坐标的XOZ面上。这样，我们把直线OP沿P点的经度线向下转动90度，到达x点，直线Ox方向就是定日镜坐标的X轴方向。

定日镜坐标的X轴和XOZ面确定了，计算S点相对于定日镜球坐标的方位角就有参照地方了。

我们把直线OP沿P点的经度线向下转动θsop度，到达T(xt，yt，zt)点。这个T点很关键，这个点对于地球的球坐标来说，方位角为φp，仰角为θp+θsop。对于定日镜的球坐标来说，方位角为零度，仰角为θsop。那么在定日镜坐标系中，T点和S点都在仰角为θsop的同仰角圆上，同仰角圆的圆心就在直线OP上的C处，坐标值为(cosθsopxp，cosθsopyp，cosθsopzp)。为了书写方便，我们将其记成C(xC，yC，zC)。连接TC、SC，因为T点对于定日镜的球坐标来说，方位角为零度，那么∠TCS就是S点相对于定日镜坐标的方位角。跟据向量夹角公式，，因为TC和SC都是同仰角园的半径。因此，所以公式可以简化为到现在我们就得到了计算太阳相对于定日镜的仰角方位角计算公式。

那么反过来呢，我们在定日镜坐标系中，观察并测量出太阳的方位角和仰角，接下来怎么能够根据这些数据，将其确定为太阳在地球哪个经纬度的正上方呢？这样的话，在一个地方阴天、观测不到太阳，而另一个地方却是晴天、能够看到太阳的情况下。就可以相互联系，相互提供太阳位置准确的标准数据。

有以上的经验，计算并不困难。如我们有某个地方，这个地方的经纬度换算成方位角和仰角后，方位角和仰角分别为(φp，θp)，测量出太阳相对于当地定日镜球坐标的方位角和仰角分别为(φs，θs)。那么我们怎么确定太阳在地球哪个经纬度处的正上方呢？如图7。

根据以前的分析，我们可以确定地球坐标的Z轴方向，相对于这个地方定日镜球坐标，方位角和仰角应该分别为180度、θp。换算成坐标值为Q(-r·sinθp，0，r·cosθp)为了书写方便，我们将其记成Q

(xq，yq，zq)。太阳方位角、仰角转化成定日镜坐标值是S(xs，ys，zs)。太阳相对于地球坐标系的仰角是∠SOQ。用向量成角公式可以计算。，由于OQ、OS都为球半径，长度为r，因此，所以公式可以简化成

我们把直线OQ沿P点的经度线向前转动θsoq度，到达T(xt，yt，zt)点，这T点对于定日镜的球坐标来说，方位角为零度，仰角为θsoq-θp)。对于地球的球坐标来说，方位角为φp，仰角为θsoq。那么T点和S点都在地球的球坐标系中、仰角为θsoq的同仰角圆上，圆心就在直线OQ上的C处，坐标值为(cosθsoqxq，cosθsoqyq，cosθsoqzq)。为了书写方便，我们将其记成C(xc，yc，zc)。连接TC、SC，跟据向量夹角公式：，因为TC和SC都是同仰角园的半径

公式可以简化为

因为T点相对于地球坐标的方位角是φp，所以S点相对于地球坐标的方位角是这样我们就计算出了太阳位置在相对于地球坐标的仰角和方位角的正上方。然后将其转换成经纬度的值，这个就很简单了。