实体膨胀管大塑性变形有限元分析

董成林

实体膨胀管大塑性变形有限元分析

董成林

（中石化中原石油工程有限公司 西南钻井分公司，成都610021）

应用有限元ABAQUS软件建立了膨胀管膨胀模型，分析膨胀过程中膨胀率、膨胀锥系统推力、膨胀长度及壁管厚变化的相对关系。分析结果表明：建立的模型可以预测膨胀管膨胀过程的推力大小、膨胀管长度以及厚度变化；当膨胀率分别为16%、20%、24%时，膨胀后厚度变化分别为6.67%、10.30%、13.16%，长度缩短分别约为4.4%、5.7%、6.2%，膨胀过程所需要的推力分别为940、1 092、1 213 k N。

实体膨胀管，厚壁圆筒，分析模型，有限元

符号说明

pc—管与膨胀锥接触面上的压力；

r—在膨胀区时随管膨胀时管的瞬时半径；

r1i—膨胀前管的内表面半径；

r1o—膨胀前管的外表面半径；

r2i—膨胀后管的内表面半径；

t—膨胀过程中管的瞬时厚度；

t1—膨胀前管的厚度；

t2—膨胀后管的厚度；

σz—管的轴向应力；

σt—管的切向应力；

σr—管的径向应力；

Fe—膨胀推力；

μ—摩擦因数；

β—膨胀锥锥角，α＝90°－β。

实体膨胀套管技术广泛用于石油钻井行业，其原理是采用刚性膨胀锥膨胀厚壁圆筒，属于大塑性变形过程。大多学者尝试着研究厚壁圆筒在不同类型载荷下的弹塑性行为［1-5］，只有较少的一些文章涉及厚壁圆筒在膨胀锥作用下的塑性变形，而涉及大塑性变形的就更少。近年来，塑性力学理论被用来研究、建立厚壁圆筒在1个圆锥工具下膨胀的分析模型［6-7］。该模型表明：膨胀过程所需要的力跟膨胀率、摩擦因数、膨胀锥的几何形状和管材的屈服强度有关。Karrech等人［8］建立了1个模型，用于预测膨胀过程中变形区的应力范围和能量损失。然而，当圆柱体的半径与厚度的比小于10时，由于从膨胀区的内表面到外表面，应力变化剧烈，横截面上的剪应力不能忽视，所以薄壁圆筒的微分方程很难得到。因此，本文以 ø193.68 mm（7英寸）、壁厚9.525 mm英寸）的标准膨胀管为例，重点研究厚壁圆筒实体膨胀管的大塑性变形（其塑性变形可以达到30%）。

1 几何模型

膨胀管膨胀系统如图1所示。随着膨胀锥在基管中移动，如果管足够长并且达到稳定状态，管中每个部分都通过了完全相同的操作。从膨胀内部取出1个微元体，根据静力平衡及体积不可压缩条件和圣维南原理使应力均匀分布，建立平衡方程。微元体的环向和径向应力分析如图2所示。

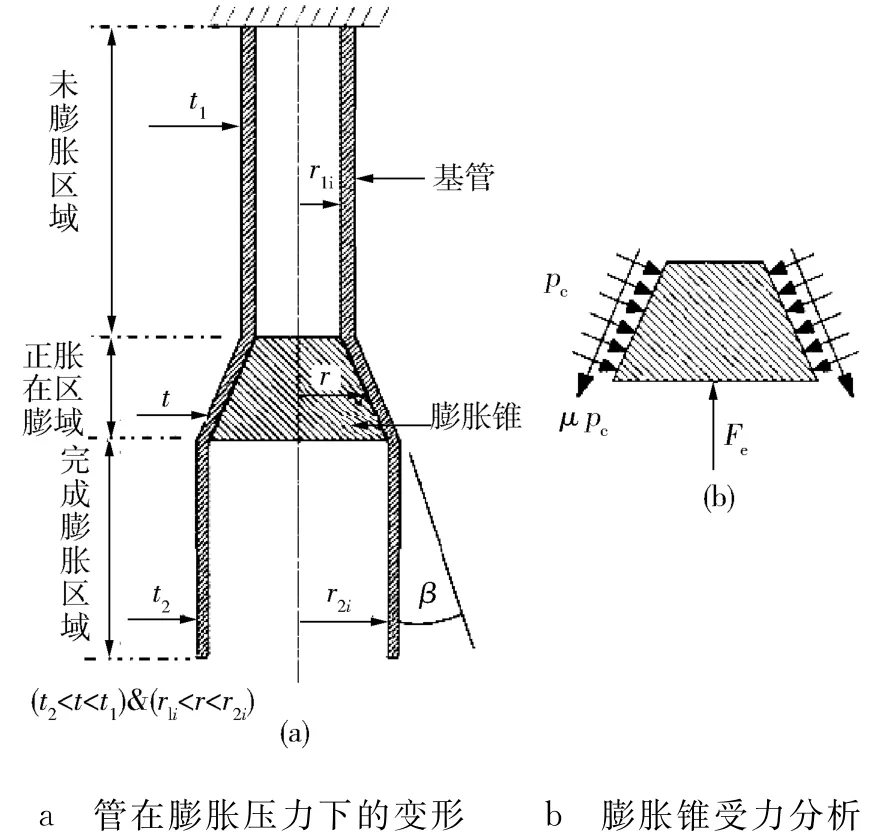
图1 膨胀管膨胀系统示意

如果使用厚壁圆筒拉梅方程（被广泛用于压力容器的设计），则开放式圆筒只有切向和径向应力存在。对于封闭圆筒，轴向应力公式可以从静力平衡方程中获得，而切向应力和径向应力的假设跟封闭式圆管相同［1］。尽管封闭式圆管从简单的静力平衡中可以看出轴向应力的存在，但是仍可以假设为零，应用开放式圆筒平面应变假设，根据切向和径向应力求出厚壁圆筒中的主应力。因此，该模型首先属于开放式圆筒模型，根据平面应力假设建立切向和径向应力的方程，然后轴向应力可以从封闭式圆筒的静力平衡中获得，并在此基础上求得主应力。

图2 微元体的环向和径向应力分析

2 条件假设

1） 在膨胀管上只有接触应力及膨胀管和膨胀锥接触表面的摩擦力。

2） 在膨胀管和膨胀锥表面上的压力是均匀分布的。

3） 管是厚壁受压膨胀模型。

4） 侧面与水平面的倾角α大于60°，这样剪应力可以忽略不计。

5） 管受径向和切向应力属于平面应力状态。

6） 管膨胀变形速率恒定。

3 有限元模型

应用ABAQUS软件对膨胀管膨胀锥系统进行模拟。与三维模型相比较，二维轴对称模型（如图3所示）既能获得合理准确的结果，也可以节省计算时间和成本。应用有限元模拟时，直到该模型获得一致收敛时结果才会变得准确。模拟分析中，膨胀管是具有弹塑性材料行为的变形体，而膨胀锥作为刚体模型，几何参数如表1。在膨胀锥与膨胀管交界面的相互作用属于库仑摩擦力模型，摩擦因数为0.075。为了能够降低摩擦因数，在基管内部涂上一种特殊的涂层，以满足实际测试要求。接触应力通过接触算法定义，在要预测的结构变形体中寻找贯穿在整个主界面上的从属节点，运用接触算法来计算接触应力。

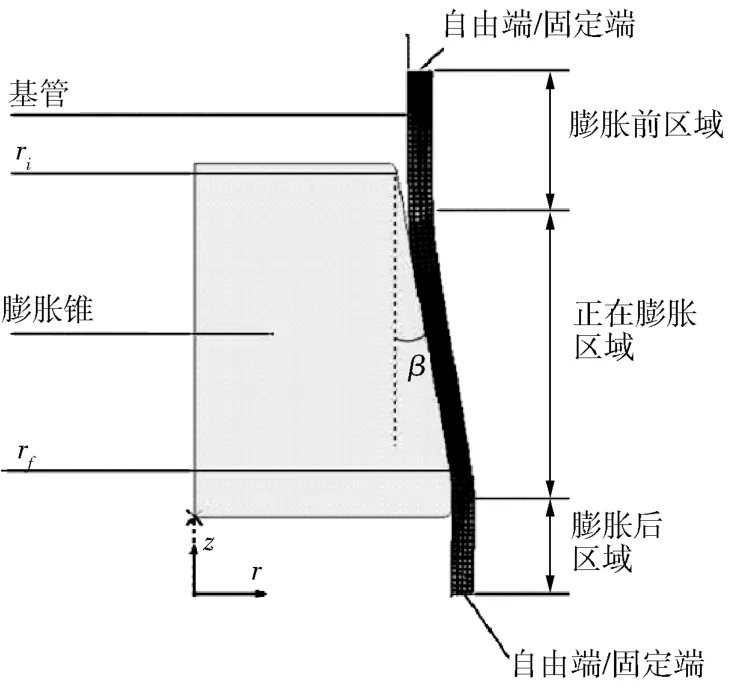
图3 膨胀管膨胀锥系统二维轴对称有限元模型

表1 有限元模型输入参数

在该模型中，为避免应力集中，圆锥体边缘倒角半径为6 mm。芯棒以0.46 m／min的固定速度自下而上运动，该速度相当于在实际膨胀试验中液压油的流量，即11 L／min。基管材料的性能是通过单向拉伸测试试验得来的，其试验样本为基管切片，该试验遵守ASTM测试标准（ASTM E8）。3个样本在万能试验机上加载拉力进行测试，直到断裂，其应力-应变曲线如图4所示。

图4 膨胀管材料应力-应变曲线

4 试验验证

4.1 试验制定

4.2 结果分析

应用有限元模型对实际测试数据进行了验证。在膨胀率为20%时，进行试验和模拟时的膨胀力数据如图5a，可以看出：通过试验获得和通过模拟获得的膨胀力相当吻合且误差小于4%；在所有情况下（其他膨胀率下），膨胀力先达到最大值（即初始膨胀过程）然后下降达到一个几乎稳态值；在膨胀率为20%的情况下，初始峰值力1 160 k N，然后在膨胀过程中的其余阶段稳定在1 092 k N；在膨胀过程中膨胀力的微小波动是一个瞬态行为，但整体在膨胀过程中是稳态的。图5b和图5c为膨胀率为20%时管的长度和厚度变化，管的厚度在膨胀前后不同的10个部位测试，并计算厚度减少的平均值，然后与仿真结果相比较。同样，长度缩短的测量和处理方法类似。在长度缩短而厚度减少的不同情况下，厚度变化率都在10%附近。总体来说，有限元模型是能够预测真实试验数据的，因此可以用来验证开发的分析模型。如图5所示。

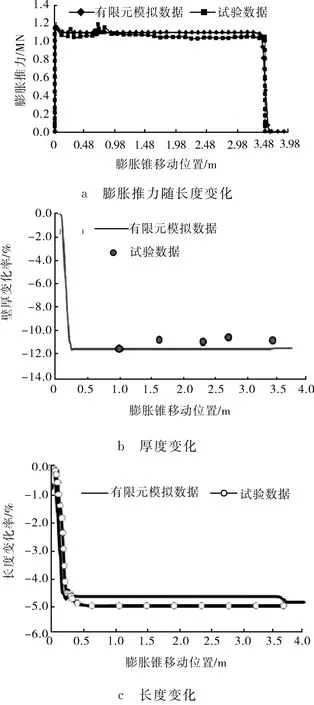
图5 膨胀率为20%时试验和有限元模拟结果对比

膨胀力、长度和厚度随膨胀率变化的关系曲线如图6所示，可以看出：膨胀力随膨胀率增加而增加，管的厚度和长度随膨胀率增加而减少，最终造成管的薄化和缩短，并在所有的膨胀率情况下大致呈线性关系；管内径膨胀到28%所需要的推力是管内径膨胀到12%时的3倍以上；膨胀率从12%到28%，导致壁厚减少8%以上，管的长度缩短3.5%以上。

图6 理论值、试验值、有限元值对不同膨胀率的计算结果对比

5 结论

1） 在运动学和平衡条件的基础上建立了厚壁实体膨胀管膨胀过程的有限元模型。

2） 有限元分析与试验结果吻合良好，膨胀率为16%、20%、24%的基管，其管厚度减少分别约为6.67%、10.30%、13.16%，长 度 缩 短 分 别 约 为4.4%、5.7%、6.2%。

3） 该结果及建立的模型可为选择合适的膨胀方法和工具提供参考，以满足特定现场的需要。

［1］ Hausenbeauer G F，Lee G C.Stress in Thick Walled Conical Shells［J］.Nuclear Engineering and design，1966（3）：394-401.

［2］ Ayob A B，Tamin M N，Kabashi Elbasher M.Pressure Limits of Thick-Walled Cylinders［C］／／Hong Kong：Proceedings of the International MultiConference of Engineers and Computer Scientists 2009，2009-03-18—20.

［3］ Darijanis H，Kargarnovin M H，Naghdabadi R.Design of thick-walled cylindrical vessels under internal pressure based on elasto-plastic approach［J］.Materials and Design，2009 （30）：3537-3544.

［4］ Perry J，Aboudi J.Elastic-Plastic Stresses in Thick-wall Cylinders［J］.ASME J.Pressure Vessel Technology，2003，125：248-252.

［5］ 张建，肖刚，孙骞，等.实体膨胀管膨胀过程数值模拟及结构优化［J］.石油矿场机械，2011，40（5）：67-70.

［6］ Al-Hiddabi S A，Seibi A C，Pervez T.Stress Analysis of Casings Expansion／Post-Expansion：Theoretical Approach［C］／／Istanbul：ASME 6th Biennial Conference Engineering Systems Design and Analysis，2002-07-08—12.

［7］ Colin G R，William C M.Analytical Model for Casing Expansion［C］／／Amsterdam：SPE／IADC Drilling Conference，2005-02-23—25.

［8］ Karrech A，Seibi A.Analytical Model for the Expansion of Tubes Under Tension［J］.Journal of Materials Processing Technology，2010，210：356-362.

Finite Element Analysis for Severe Plastic Deformation of Solid Expandable Tube

DONG Cheng-lin
（Southwest Drilling Company，Sinopec Zhongyuan Oilfield Service Corporation，Chengdu 610021，China）

FEA ABAQUE was applied to establish expandable tube model，and the correlation of expansion rate，expansion cone thrust，expansion length and wall thickness.The result shows that thrust，length and thickness could be predicted by using the established model.At the expandable rate of 16%，20%，and 24%，expandable thickness change is 6.67%，10.30%，and 13.16%；length shorten is 4.4%，5.7%，and 6.2%；and the thrust needed is 940，1 093，and 1 213 k N respectively.

solid expandable tube；thick-walled cylinder；analysis model；FEA

TE931.2

A

1001-3482（2014）03-0043-05

2013-09-13

董成林（1971-），男，河南林州人，工程师，主要从事石油工程及钻井设备管理工作。