基于复合形法的提管架夹紧机构优化设计

杨 磊，于 爽，段梦兰

基于复合形法的提管架夹紧机构优化设计

杨 磊1，于 爽2，段梦兰1

（1.中国石油大学（北京）海洋油气研究中心，北京102249；2.中海油田服务股份有限公司 钻井装备建造管理项目组，河北 燕郊065201）

海底管道在铺设和使用期间可能会发生泄漏、屈曲或灾难性的破坏。对损坏的海底管道进行应急维修时，要用提管架将管道提离海床，为使用其他维修设备进行维修提供作业空间。管道夹紧机构是提管架的重要机构，采用复合形法对管道夹紧机构进行优化计算，根据优化对象建立了优化数学模型；确定设计变量，建立了目标函数；建立了以不等式形式给出的约束条件；应用Matlab编写优化程序，迭代求得最优解。

提管架；夹紧机构；优化设计；复合形法

管道是目前海洋石油运输的主要工具。深水海底管线在安装、运行中可能受海流、波浪的冲刷及介质腐蚀，油气运输过程中管道产生振动以及过往船舶的落物、锚、拖网的撞击等因素的影响，发生结构变形或管线损坏，从而影响生产甚至造成巨大经济损失，促使了深水海底管线维修系统（DPRS，包括维修技术、工具和设备、方案及系统管理等）的研究与发展［1］。DPR主要由Sonsub、Stress Subsea、Oil States、Oceaneering、Statoil Hydro等公司研究开发，在管线维修方面有着成熟的方案和系列化、标准化的维修工具及设备。

海底管道的常用维修方法有夹具维修、海底维修、海上提管维修、海底维修与海上提管维修相结合的方法或者重新铺设管道［2-4］等。

对于深水管道维修，常用到夹具维修和海底维修。前一种适合于管道发生小泄漏时的维修；后一种适合于短管道更换的维修。这2种维修方法都需要将管道提离海床，因此提管架（Pipeline Life Frame，简称PLF）是海底管道维修不可或缺的设备。

夹紧机构是提管架最重要的组成部分，它不仅要实现夹紧松开功能，还要有自锁功能，防止提升过程中管道松脱。在满足功能和强度要求的前提下，对夹紧机构进行优化设计，能提高产品质量、降低制造成本、减少结构尺寸。

1 提管架的功能与结构

1.1 功能

提管架主要作用是将破损的管道提离海床并保持一定高度，为其他维修作业机具提供作业空间，作业完成后将管道放回海床［5］。

深水维修作业通常使用ROV（Remote Operated Vehicle）辅助其他设备进行作业。提管架通过维修船舶上的吊机和绞车下放入水，在ROV的引导下到达作业地点。由于受海流、海底视野差、远程操控精度等因素的影响，提管架下放位置与管道轴线位置有误差。ROV通过快插接头与提管架控制面板连接为其提供液压源，ROV操控提管架横向移动和转动机构将夹紧机构调整到合适的位置，夹紧管道；ROV操作垂向移动机构将管道提升。保持管道的提升高度，进行维修作业。维修完毕后，下放管道，回收提管架。

1.2 整体结构

不同厂家生产的提管架在结构上有所差异，但基本功能相同。本文针对作者自主设计的深水提管架进行优化设计。该提管架提升管道直径203.2～304.8 mm（8～12英寸）、最大提升高度2.44 m（8英尺），整体结构如图1所示。该提管架有1个灵活的夹紧机构，它有转动、横向移动功能，能够方便地调整夹子到合适的夹持位置。提管架的垂向移动机构实现管道的提升运动；转动机构可以使夹子绕垂线转动一定的角度；横向移动机构可以使夹子在中垂面附近移动；伸缩式套筒液压缸使夹子在垂直方向移动。

图1 提管架整体结构

1.3 夹紧机构

提管架夹紧机构简称夹子，由2个大液压缸、4个小液压缸（前面与后面各2个）、4个小滑块、2个对称的爪子和夹子基座组成，如图2所示。

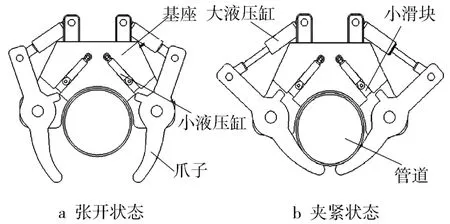
图2 夹子夹持原理

2个大液压缸用于推动爪子抱紧管道，4个小液压缸用于推动小滑块锁住爪子，使其维持在夹紧状态。夹子的动作是提管架的主要运动，它与提管架的工作时序相关，故夹紧动作顺序是：首先保证夹子处于打开状态→下放夹子→调整到合适的位置→合拢爪子夹紧管道→提升管道到一定高度→维修→下放夹子→打开夹子。其打开与夹紧的过程如图3所示。

锁紧原理如图4，用黑色圆圈标出小滑块伸出的位置。小滑块嵌在基座上所开的滑槽上，夹子合拢后，小滑块才由小液压缸推动沿滑槽滑出，卡住爪子，将提升力传递到基座上。

图3 夹子打开与夹紧过程示意

图4 夹子锁紧原理

2 夹紧机构的优化设计

2.1 数学模型的建立

夹紧机构是提管架的重要承载机构。在满足强度条件下，对提管架各机构进行优化设计，可以减少结构总体质量，降低制造成本。夹紧机构由于提升管道尺寸和功能的限制，对其垂直截面尺寸优化意义不大。但是对夹紧机构的水平截面进行优化，例如基座的壁厚及与旋转机构相连接的内螺纹直径，可以减轻机构质量。设计变量、目标函数和约束条件是组成优化设计数学模型的3个要素。

2.1.1 设计变量的确定

提管架通过中心螺纹孔与转动机构相连，螺纹承受所有的提升力及夹子自重。根据设计时提供的数据，管道的最大提升力为100 k N，综合考虑海底高压低温及海流等的影响，工况系数取2.0，则设计载荷为200 k N。以螺纹公称直径和基座最小壁厚为设计变量，如图5所示。

图5 设计变量

2.1.2 目标函数的确定

对于此优化问题，希望减轻夹子的总体质量。液压缸为选型采购，不在优化范围内。夹子的主要质量集中在基座、爪子和爪子销轴上，质量与所选材料密度、物体体积有关。设计时考虑到45调质钢的良好综合性能，选用此材料来加工基座、爪子和爪子销轴。材料确定则目标函数可表示为夹子的体积。为了满足夹子的功能要求，不更改如图4所示的截面尺寸。由于其他尺寸不变，要使夹子的体积最小，则它的顶部截面最小，则可以以此作为目标函数。顶面截面由1个矩形减去1个圆组成，则目标函数为

2.1.3 约束条件的确定

在选取约束条件时应当避免出现相互矛盾的约束，尽量减少不必要的约束。不必要的约束不仅增加优化设计的计算量，而且可能使可行域缩小，影响优化结果［6］。

所设计的提管架用于深海中（水深1 500 m），考虑到海水的腐蚀性，在设计时要加入腐蚀余量，取腐蚀余量3 mm。选用45钢为提管架主要材料，其屈服应力为σs＝353 MPa，σb＝598 MPa。由机械设计手册中查得，45钢的屈服应力与强度极限之比为0.59，对应的最小许用安全系数是1.4～1.8。由于海洋环境的复杂性，载荷和应力计算不准确，故在最小许用安全系数的选择上加大20%～50%。在最小许用安全系数的基础上增加20%，故取安全系数S＝1.8。以屈服极限作为极限应力，则

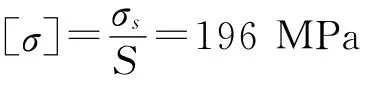
对于一般的塑性材料，其剪切应力极限为0.6～0.8倍的极限正应力。选择中间值0.7，则

1） 几何约束条件。

由图5可以看出，夹子的壁厚不能小于液压缸支座宽度，则

螺纹孔径不能与液压缸支座干涉，则

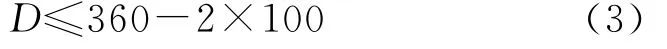
由设计参数爪子厚度大于45 mm，所选液压缸厚度为35 mm，为满足装配要求，则

2） 螺纹强度约束条件。

对于此夹子优化问题，螺纹应满足强度要求。夹子基座的截面形状比较复杂，下面进行简化计算。与基座相配合的螺纹柱是1个环形圆柱，壁厚10 mm；此螺纹柱的外径为D1，内径D2＝D1－0.02，螺纹危险截面拉伸应力为

式中：F′为螺纹所受轴向力，即设计载荷。

扭转剪应力为

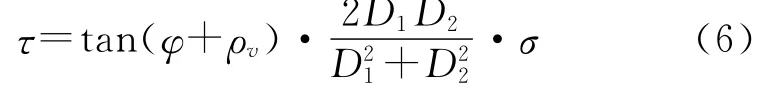
根据第四强度理论，有

考虑螺纹的应力集中，45钢的螺纹应力集中系数为K＝1.9。故螺纹的最大应力为

要满足强度要求，则

由式（5）～ （9），代入D1和D2，螺纹中径升角φ＝2°30′，当量摩擦角ρv＝8°32′，考虑3 mm的腐蚀余量，则螺纹公称直径D≈D1≥45.8 mm。

3） 截面抗拉强度约束条件。

此截面壁厚不均匀，壁厚最小的地方容易出现破坏，故将其简化为1个外径为D＋2d、内径为D的圆环；如果它能满足抗拉强度要求，则此截面也能满足要求。

简化截面积为

截面应力为

由上述两式并考虑3 mm的腐蚀余量，得

对于式（12），d随着D的增大而减小，将D的最小值45.8 mm代入此式，得d≥9.2 mm。

综上所述，用x1代替螺纹公称直径D，用x2代替基座最小壁厚d，得到提管架夹紧机构优化设计的数学模型为

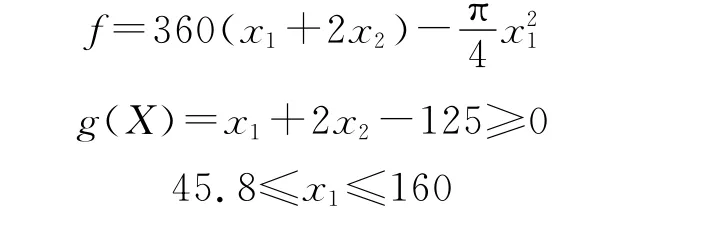
求最最优值X*＝［x*1，x*2］，使

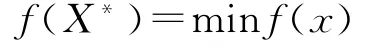
2.2 复合形法优化原理

复合形法是在单纯形法的基础上发展起来的。它的基本思想是在可行域内构造n＋1～2n（n为设计变量的个数）个顶点，比较各顶点的函数值，从函数值的大小可以判断函数变化的大致趋势，丢掉最坏点，代之以好点，构成新的复合形，然后逐步逼近最优点［6］。

2.3 复合形法优化过程

1） 对于优化数学模型，由约束条件g（X）构成的可行域，有2个设计变量x1（螺纹公称直径）和x2（基座最小壁厚）。在可行域内随机生成初始顶点，利用计算机随机生成其他3个顶点。这4个顶点构成至少有2个线性独立的矢量。当随机构造的点不在可行域内时，可以用收缩的方法靠近形心点，公式为［3］

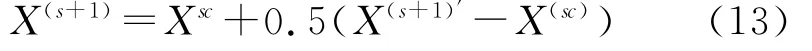
式中：X（sc）为在可行域内所有点的形心；X（s＋1）′为不在可行域的点；X（s＋1）为新构造点。

循环使用式（12）计算，直到其他3个随机生成的顶点在可行域内为止。

2） 计算复合形各顶点的函数值，找出最坏点、次坏点、最好点。除去最坏点，再计算新的形心，如果在可行域内，进行反射计算，计算公式为［3］

式中：X（r）为反射点；X（c）为可行域内除最坏点以外的形心；X（h）为最坏点；α为反射系数，初始值一般为1.3。

如果形心不在可行域内，则以最好点为起点，形心为终点重新利用伪随机数产生新的复合形。

3） 计算反射点和最坏点的目标函数值。如果f（X（r））＜f（X（h））则用反射点替换最坏点，反之将反射系数减半，利用式（13）重新计算反射点，再进行比较。如果反射系数过小，则用次坏点代换最坏点进行反射计算。

4） 计算各点目标函数值与最好点之差的均方根，并与给定误差比较。如果大于误差，则重复步骤2～3。如果小于误差，迭代终止，最好点即为最优解。

2.4 优化程序的编制与计算过程

本文采用Matlab进行编程，根据第2.3节的复合形法优化过程，其程序流程［6］如图6所示。

根据程序流程图编写了3个函数：复合形法主程序Complex M（）；目标函数myfun（x）；点是否在 可行域内的判断函数fok（）。

图6 复合形法程序流程

程序初始数据为：顶点数k＝4，设计变量数n＝2，误差er＝0.000 001，反射系数初始值arf＝1.3，反射系数最小值kse＝0.01。在Matlab工作空间输入［XMin，f Min］＝ Complex M（），回车运行即可。程序运行结果如图7所示。

图7 程序计算结果

2.5 计算结果的分析

如图7所示，同一个程序，2次计算过程生成的随机点不同，误差不同，优化计算步数也不同，但结果相同。最优点均为X*＝［106.6 9.2］，即螺纹孔直径为106.6 mm，基座壁厚为9.2 mm。最优点正好在边界g（X）＝x1＋2x2－125≥0上。目标函数、约束函数均是凸函数，只有1个全域约束最小点，此点经常出现在边界上，因此计算结果可靠。

目标函数最小值f（X*）＝3.607 5×104。提管架初始设计尺寸螺纹孔直径为120 mm，基座壁厚为20 mm，截面积为f（X0）＝4.629 0×104。优化结果截面积减少22%。从而提管架夹紧机构质量可减少1／5左右。

3 结论

1） 在考虑海洋工况和腐蚀余量的情况下，利用复合形法，对提管架的夹紧机构顶截面进行了优化计算。使用随机生成的初始点，经多次计算验证，得到相同的最优解，计算结果可靠。

2） 对提管架夹紧机构顶截面进行了优化计算，模型上做了合理的简化，所得的最优解有一定参考价值。如果要对提管架整体进行优化，需要对各部分进行合理化分，分别进行优化，最后得到最优解。

3） 复合形法程序实现简单，计算效率高，计算结果可靠。复合形法适合于尺寸、强度等约束条件以不等式给出的机械结构优化设计，应用前景广泛。

［1］ 梁富浩，李爱华，张永祥，等.深水海底管线维修系统研究进展及有关问题探讨［J］.中国海上油气，2009，21（5）：352-357.

［2］ Rob Martin，INTEC Engineering，Joseph Killeen，BP A-merica，Inc.Bruce Chandler，INTEC Engineering .Mardi Gras Deepwater Pipeline Repair System ［R］.2004，OTC 16635.

［3］ Rebello A，Ayers R，Stress Subsea.A Low-Capex Deepwater Pipeline Repair System for the Gulf of Mexico［R］.2006，OTC 17772.

［4］ 张剑波，袁超红.海底管道检测与维修技术［J］.石油矿场机械，2005，34（5）：6-10.

［5］ Killeen J，Taconis T，Whipple J，Chandler B.Large diameter deepwater pipeline repair system ［G］.DOT，2006.

［6］ 梁尚明，殷国富.现代机械优化设计方法［M］.北京：化学工业出版社，2005：102-107.

［7］ 陈家庆，焦向东.水下破损管道维修技术及其相关问题［J］.石油矿场机械，2004，33（1）：33-3.

Optimization Design Research of PLF’s Clamping Mechanism Based on the Complex Method

YANG Lei1，YU Shuang2，DUAN Meng-lan1
（1.Of fshore Oil and Gas Research Center，China University of Petroleum，Beijing 102249，China；2.Drilling Equipment Construction Management Project Team，COSL，Yanjiao 065201，China）

Subsea pipeline may happen leak，buckling or catastrophic failure during the laying and use period.In order to provide space for other repair tools，PLF is used to lift the pipe off bottom when repairing the damaged subsea pipeline.The application of the complex method in the pipe clamping mechanism optimization calculation is studied.According to the optimized object optimization，mathematical model is established and the design variables are determined.Objective function is established.As given in the forms of inequality constraint conditions are established.Then Matlab is used to write optimization program and obtain the iterative optimal solutions.

pipeline life frame；clamping mechanism；optimization design；complex method

TE973.8

A

1001-3482（2014）03-0037-06

2013-09-23

国家科技重大专项（2011ZX05027-005-001）；国家自然科学基金青年基金（51309235）

杨 磊（1987-），男，江西玉山人，硕士，主要从事海洋石油装备的设计理论与方法研究，E-mail：yanglei1987120＠126.com。