高压压裂油套环空井压降计算
2014-12-11孙宝龙王春生庞博学冯昭森
刁 宇,孙宝龙,王春生,康 健,庞博学,冯昭森
设计计算
高压压裂油套环空井压降计算
刁 宇1,孙宝龙2,王春生1,康 健1,庞博学1,冯昭森3
(1.东北石油大学 石油工程学院,黑龙江 大庆163318;2.中石油西气东输管道公司,上海200000;3.中国石油天然气管道局,河北 廊坊065000)
应用达西公式、伯努利方程等建立了数学模型,进行压降计算的数值模拟;编写了压降计算程序,实现软件编程模拟,并针对ø63.5 mm(2⅟²英寸)油管和ø76.3 mm(3英寸)油管进行压降分析。结果表明:随着管径的增大,流速增大,沿程水头损失与局部水头损失均显著增加,最终导致压降增大;此压降若超过运行条件允许的范围,会造成压裂施工停止、油井停产、管道停输等严重事故,影响正常生产,因此对流体在环空管道中的流动阻力以及压降进行准确的计算至关重要。
环空;压降;数值计算;阻力损失
在油井的增产改造中,水力喷射压裂技术具有明显优势。通常由于油管管径、流体排量、流体密度或黏度等的影响,使沿程阻力损失和局部阻力损失发生变化,会产生较大的油套管环空管线的压降。在高压压裂过程中,压裂液都是通过油套环空管段送至井下的。精确地掌握生产过程中的压降至关重要,目前常规的处理方法是将环空管道转化为具有当量直径的圆形管道进行计算,这种方法简便易行。本文应用达西公式、伯努利方程等进行数值计算,分析了影响压降的主要因素,并对高压压裂的油套环空管线进行优化。
1 环空井压降计算理论研究
液体在井下油套管环空管线中流动,由于摩擦耗能,使液体压力下降,产生沿程水头损失;同时又流经连接2段油管的接箍,流通面积突然缩小又突然扩大,产生局部阻力损失。这2种损失是产生压降的原因。
1.1 当量直径及流速计算
流体力学中将有效断面面积与湿周长的比值称为水力半径,以Rh表示。本文计算的油套管环形截面的水力半径为
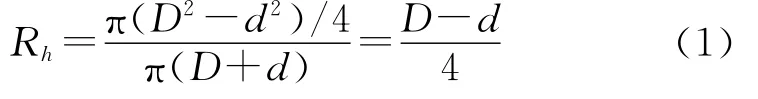
式中:D为套管内径;d为油管或接箍外径。折算后当量直径为

环空流速为
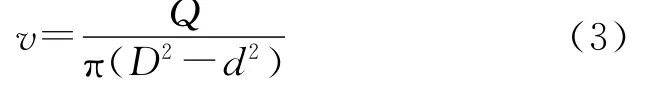
式中:Q为环空排量。
1.2 不同流态区摩阻系数的计算
管路的沿程阻力损失hf可按达西公式计算,即

式中:λ为水力摩阻系数;L为管路长度;g为重力加速度;v为流速。
水力摩阻系数λ随流态不同而不同,理论和试验都表明:水力摩阻系数是雷诺数Re和管壁相对当量粗糙度ε的函数。雷诺数表示流体中惯性力与粘滞力之比。则
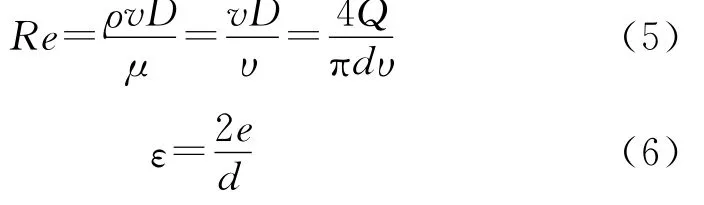
式中:μ为动力黏度;υ为运动黏度;e为管壁的绝对当量粗糙度。
流体在管路中的流态按雷诺数来划分,在不同的流态区,水力摩阻系数与雷诺数及管壁粗糙度的关系不同,雷诺数是作为判别流体流动状态的准则,根据不同的雷诺数作出对应的流态判断。
1.3 综合参数摩阻计算公式
使用达西公式计算沿程摩阻,由于λ与Re和ε有关,不便分析各参数对摩阻的影响。对达西公式中的各个参数进行重新整理,可得到便于使用的综合参数摩阻计算式,即列宾宗公式,有
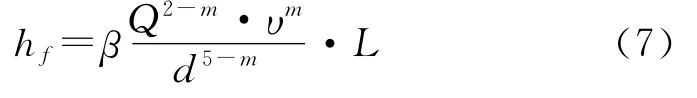
该摩阻计算式反映了沿程摩阻与流量Q、黏度、管内径d、管长L间的相互关系。
1.4 局部阻力损失
在液流断面急剧变小或变大的地方会产生局部阻力,引起局部水头损失。管道上安装了连接油管的接箍,流速重新分布,产生局部阻力损失。计算式为

突缩系数为
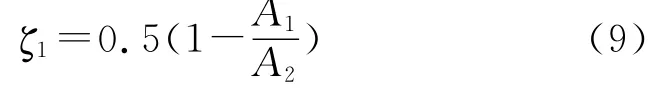
式中:A1、A2分别为油、套管环空截面积。
则突缩管局部阻力损失为

突扩系数计算如下。
1) 方法一。

2) 方法二。

则突扩管局部阻力损失为

总的局部水头损失为突缩管局部损失与突扩管局部损失2部分之和,即

1.5 环空管道的压降计算
对管内径d和管长L一定的某管道,当输送一定量的液体时,由起点至终点的总压降可根据流体力学中伯努利方程进行计算,即
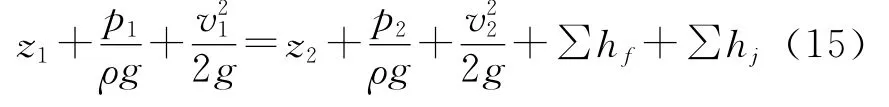
式中:z1为井口高程;z2为井底高程;p1为井口压力;p2为井底压力;v1为井口平均流速;v2为井底平均流速;∑hf、∑hj分别为总沿程水头损失、总局部水头损失。
整理后油套管环空压降为
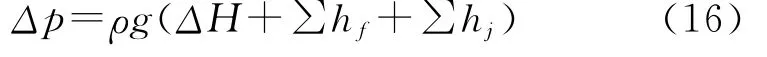
式中:ΔH为井深。
2 实例计算及分析
2.1 计算参数
本文以中国石油集团渤海钻探工程有限公司现场数据为依据进行计算分析。

表1 套管数据 mm
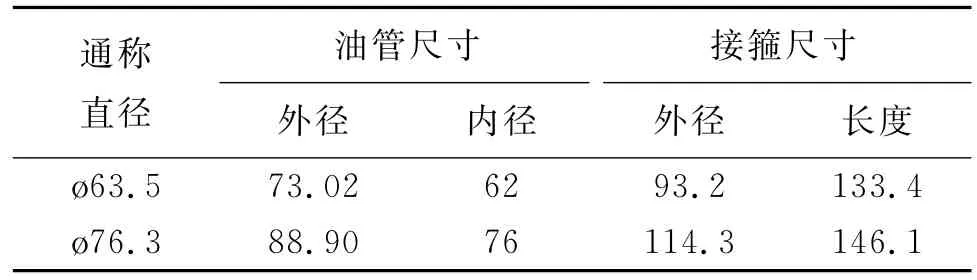
表2 油管数据 mm
已知油井的环空排量为0.5 m3/min,液体密度为998.2 kg/m3,液体的动力黏度为1.005 mPa·s,接箍共有159个,管柱总长1 526 m,压裂液密度一般在950~1 050 kg/m4,压裂液黏度一般是0.995~1.010 mPa·s。
2.2 压降与排量及压裂液密度的关系
压裂液的动力黏度为1.005 mPa·s时,ø63.5 mm(2⅟²英寸)和ø76.3 mm(3英寸)油管的环空压降随着压裂液密度和排量的增大而不断增加,但两者都很均匀,如图1~2所示。
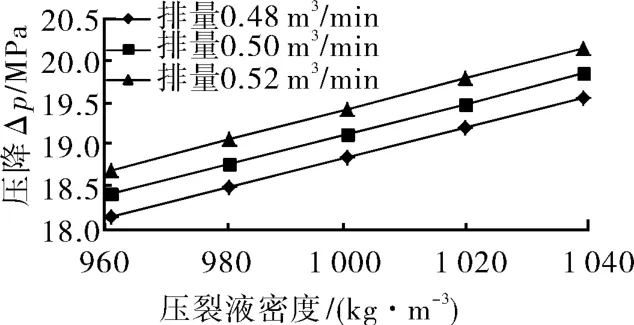
图1 ø63.5 mm油管压降与排量及密度的关系曲线

图2 ø76.3 mm油管压降与排量及密度的关系曲线
2.3 压降与排量及压裂液黏度的关系
压裂液的密度为998.2 kg/m3时,ø63.5 mm(2⅟²英寸)和ø76.3 mm(3英寸)油管的环空压降随着压裂液黏度和排量的增大不断增加,并且非常平缓。如图3~4所示。
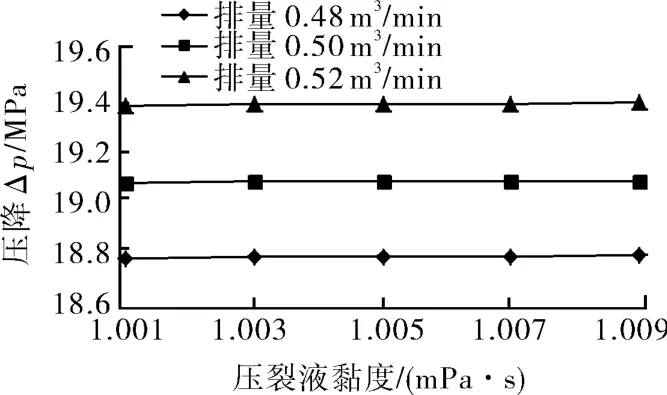
图3 ø63.5 mm油管压降与排量及黏度的关系曲线
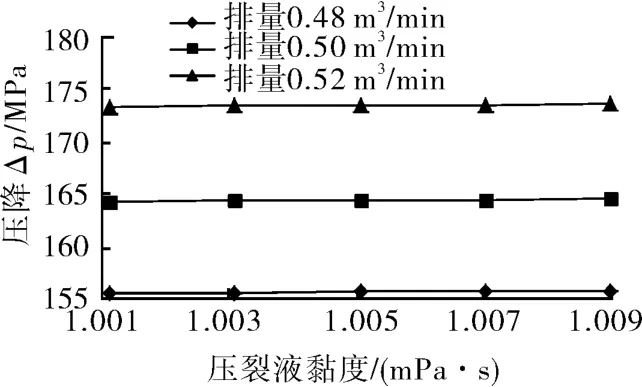
图4 ø76.3 mm油管压降与排量及黏度的关系曲线
2.4 压降与压裂液密度和黏度的关系
压裂液的排量为 0.5 m3/min时,ø63.5 mm(2⅟²英寸)和ø76.3 mm(3英寸)油管的环空压降随着压裂液黏度的增大而不断增加,压降随着压裂液密度的增大变化并不明显,几乎重合。如图5~6所示。
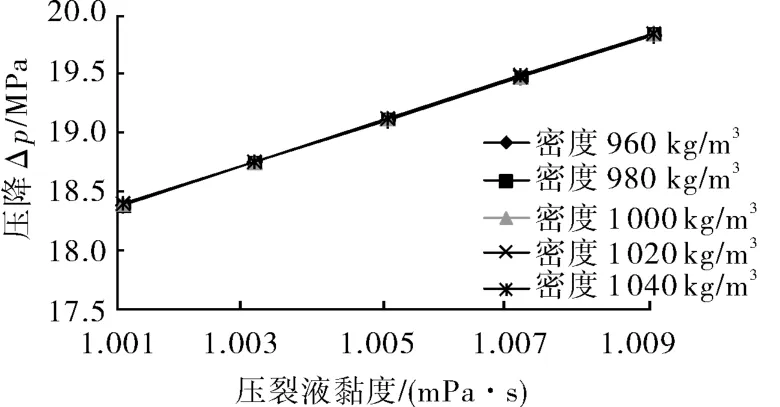
图5 ø63.5 mm油管压降与密度及黏度的关系曲线

图6 ø76.3 mm油管压降与密度及黏度的关系曲线
3 优化建议
对于给定的流量,油管管径的大小与地下管道系统的一次投资费、操作费等项有密切的关系,应根据这些费用做出经济比较,以选择合适的油管管径。此外,管径的大小还对沿程水头损失与局部水头损失造成影响,如果忽略这种影响,可能会对系统的安全造成隐患。
4 结论
1) 实现了数值模拟和软件编程模拟计算环空压降;将压降影响因素绘制成图表,分析排量、压裂液密度和黏度对压降的影响。
2) 针对ø63.5 mm(2⅟²英寸)和ø76.3 mm(3英寸)油管进行压降分析,套管内径保持不变,油管和接箍外径增大,环空截面积减小,排量保持不变,流速增大,沿程水头损失与局部水头损失均显著增加,最终导致压降增大。
3) 建立高压压裂油套环空井压降模型,压降模型的计算准确性需从局部阻力系数及沿程阻力系数等角度进行修正。
[1] 蒋廷学.压裂施工中井底压力的计算方法及其应用[J].天然气工业,1997(9):81-84.
[2] 吴宁,宿淑春,陈超.水平井筒变质量环空流压降分析模型[J].西安石油学院学报,2001,16(6):16-18.
[3] 鲁港,王立波,王冠军.幂律流体液同心环空轴向层流压降的计算[J].断块油气田,2009,16(4):127-129.
[4] 褚元林.钻井环空固液两相流压降模型理论分析[J].石油大学学报,1996,20(6):16-19.
High Pressure Casing Annulus Well Fracturing Oil Pressure Drop Calculation
DIAO Yu1,SUN Bao-long2,WANG Chun-sheng1,KANG Jian1,PANG Bo-xue1,FENG Zhao-sen3
(1.College of Petroleum Engineering,Northeast Petroleum University,Daqing 163318,China;2.West-east Gas Pipeline Company of CNPC,Shanghai 200000,China;3.China Petroleum Pipeline Bureau,Langfang 065000,China)
By using Darcy formula,Bernoulli equation mathematical model is established,the pressure drop calculation of numerical simulation.The pressure drop calculation program was written and the software programming simulation was realized.3 inches for 2 and a half inch tubing and tubing pressure drop is analyzed,with the increase of pipe diameter,flow rate increases,frictional head loss and the local head loss were significantly increased,eventually leading to the pressure drop increases.If the pressure drop exceeds the range of operating conditions,this will cause the fracturing construction stopped,the oil well production,and pipeline,such as serious accidents,affecting the normal production.So the fluid in the annular pipe flow resistance and pressure drop for the accurate calculation is of crucial importance.
annulus;pressure drop;numerical calculation;resistance loss
TE931.2
A
1001-3482(2014)03-0026-04
2013-09-03
国家自然科学基金“超重力流化床气固相间作用机理与颗粒流矩模型的研究项目”资助(21076043)
刁 宇(1988-),男,辽宁锦州人,硕士研究生,主要从事热流固耦合及物模实验研究,E-mail:284883555@qq.com。
