基于模块化思想的复杂故障树重要度算法研究
2014-12-10黄智伟梁奕坤张三娣
黄智伟,梁奕坤,张三娣
(工业和信息化部电子第五研究所,广东 广州 510610)
0 引言
底事件的重要度是故障树的一个重要特性。工程实践表明,导致系统故障的各部件并不是同等重要的,重要度可用于表示某个部件对顶事件的影响大小,重要度对改进系统设计,制定维修策略是十分有用的[1]。
随着装备系统的复杂程度越来越高,构造出来的故障树也越来越庞大和复杂。存在共因事件的静态故障树一般采用二元决策图 (BDD)分析计算,动态故障树则需要转换为马尔科夫链进行计算,庞大的二元决策图和马尔科夫链都会引起NP问题。为了避免将复杂故障树整体转换为二元决策图或马尔科夫链,需要根据故障树结构将其拆分成可独立计算的模块,再将各模块的计算结果合并[2]。
模块化思想在计算故障树顶事件发生概率时已经被广泛地应用,但是,在计算故障树重要度尤其是结构重要度时存在一定的困难,例如:如何合并模块化后的重要度?以及概率重要度和结构重要度的计算过程有何区别?本文将详细地介绍如何应用模块化思想求解复杂故障树的重要度。
1 故障树重要度计算的基本原理
故障树重要度一般包括结构重要度、概率重要度和关键重要度,关键重要度可通过事件发生概率和概率重要度求得,因此,本文只介绍结构重要度和概率重要度的计算方法。
结构重要度指的是故障树中某个元素其正常状态与不正常状态相比,在系统所有可能的状态数中,正常状态数增加的比例[3]。其计算原理为:

式 (1)中:Gi——第i个事件的结构重要度;
P顶事件——顶事件的发生概率;
Pi——第i个事件的发生概率。
概率重要度指的是某元素从不正常状态转为正常状态时,系统的不可靠度改善了多少[3]。其计算原理为:

式 (2)中:Ii——当前事件的概率重要度;
P顶事件——顶事件的发生概率。
根据计算原理可得,计算重要度最直接的方法是通过改变事件的发生概率,求得顶事件发生概率即可。因此,所有的计算工作都在于重复计算顶事件的发生概率。
假设计算一次顶事件的发生概率所耗费的资源(包括计算机内存和时间等)为S,则包含N个基本事件的故障树结构重要度计算将耗费的资源为2N*S。
实验表明,应用二元决策图或最小割集法计算一个包含2000个底事件的故障树大约需要1 min的时间,则计算所有底事件的结构重要度需要50 h,这在故障树设计阶段是不可接受的,因此,不可直接用此方法计算复杂故障树。
模块化方法可以在计算顶事件发生概率的同时,计算模块子树中各个底事件重要度,所以耗费的时间与计算顶事件发生概率时间相等。
2 基于模块化的重要度计算方法
2.1 模块化思想
基于模块化思想的方法在故障树分析计算方面的效果显著,本文介绍重要度的计算方法也是基于模块化思想提出的,以下面的故障树为例,如图1所示。

图1 故障树示例
从图1可以看出,x1和x5是共因事件,因此G3、G4、G6、G7不能作为独立模块。而x1包含在G2中,x5包含在G5中,并且G2和G5与其他节点没有相同子节点,所以可作为独立模块进行分析计算,再将计算结果合并到顶事件G1。
假设故障树的底事件为x1,x2,…,xn,则故障树可表示为:

式 (3)中:x1,x2,…,xn——独立的事件,将故障树模块化之后包含的模块子树为M1,M2,…,Mn,可表示为:

因此,由式 (4)可以得到图1中的故障树可表示为:

模块化后由于G2和G5存在共因事件,可用较优的BDD算法求解,而后将G2和G5当作独立事件,再用常规算法求解顶事件G1。
此处建议把故障树分解到最小单位,将所有独立的节点都作为模块计算,即图1中的故障树中的模 块 包 括 G1, G2, G3, G4, G5, G6, G7, x1, x2,…,x6。计算重要度时,应采取从下往上的递归方法。先求出底事件相对于模块的重要度Imodule(x),再求出该模块相对于系统的重要度Isys(M),合并后可得到底事件相对于系统的重要度[4-5]:

模块化思想计算复杂故障树重要度的流程如图2所示,单个模块子树的重要度算法在此处不做详细介绍。

图2 基于模块化思想的故障树重要度算法流程
2.2 结构重要度
以图1为例,假设将一个独立事件的结构重要度表示为G,计算G2模块中x1的重要度时,将x1的概率设置为0,其他事件的概率设置为0.5,得到f(x1=0)=0,同样得到f(x1=1)=0.75,通过式(1)可得事件x1在模块G2中的结构重要度为f(x1=1)-f(x1=0)=0.75,以此类推可得到G2模块中各事件的结构重要度为:

此处需引入一个定义:结构重要度权值W。
本文将结构重要度权值定义为当前模块在仅受其基本事件的结构影响时的发生概率。结构重要度权值的计算方法为,将所有基本事件的概率Pi设置为0.5,得到的概率值即是该模块的结构重要度权值,即:

即单一事件的结构重要度权值W (x)=0.5。
在计算G1中各事件的结构重要度时,将G2作为单一事件,此时G2模块的结构重要度权值已经不是0.5,通过计算可得W (G2)=0.375。根据式(1) 计算时,G2的发生概率应该设置为W (G2)。可得到G1模块中各事件的结构重要度为:
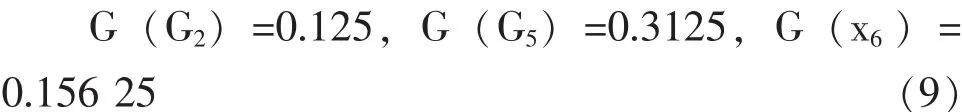
根据模块化合并思想由式 (7)和 (9)可得事件x1、x2、x3在顶事件G_1中的结构重要度为:

同理可递归计算所有的事件在整个故障树中的结构重要度。
2.3 概率重要度
以图1为例,假设将一个独立事件的概率重要度表示为I,并且图1中的所有事件发生概率为0.1,则在计算G2模块中x1的重要度时,将x1的概率设置为0,其他事件的概率保持不变,得到f(x1=0) =0, 同样得到 f(x1=1) =0.19, 通过式 (2)可得事件x1在模块G2中的概率重要度为f(x1=1)-f(x1=0)=0.19,以此类推可得到G2模块中各事件的概率重要度为:

与计算结构重要度相同,在计算G1中各事件的概率重要度时,将G2作为单一事件,先计算G2的发生概率,应用式 (2)可得到G1模块中各事件的概率重要度为:
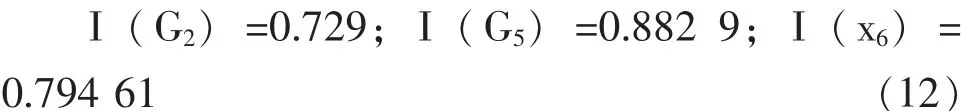
根据模块化合并思想由式 (11)和 (12)可得事件x1、x2、x3在顶事件G1中的概率重要度为:

同理可递归计算所有的事件在整个故障树中的概率重要度。
2.4 模块化求解故障树重要度算法的实现
a)FUNCTION计算故障树重要度
计算独立模块重要度 (Top);
合并独立模块重要度 (Top);
END FUNCTION。
b)FUNCTION计算独立模块重要度 (Node)
遍历Node的子节点Child;
计算独立模块重要度 (Child);
结束遍历。
c)IF当前节点被定义为独立的模块THEN
计算Node发生概率;
计算Node结构重要度权值;
遍历当前节点的底事件;
计算底事件的重要度;
结束遍历;
将Node标记为事件节点;
END IF;
END FUNCTION。
d)FUNCTION合并独立模块重要度 (Node)
遍历Node的子节点Child;
合并独立模块重要度 (Child);
结束遍历。
e)IF当前节点被定义为独立的模块THEN
遍历当前节点的底事件;
合并当前模块基本事件的结构重要度;
合并当前模块基本事件的概率重要度;
结束遍历;
END IF;
END FUNCTION。
2.5 应用五所工程软件CARMES 6.0验证计算结果
五所工程软件CARMES中包含了故障树分析模块,有广泛的工程应用经验,在国内外质量与可靠性软件行业具有很大的影响力。
在CARMES 6.0中建立如图1所示的故障树,将所有的底事件发生概率设置为0.1,进行分析计算后可见,计算结果与前文中应用模块化思想分析计算故障树重要度的结果一致。如图3所示:
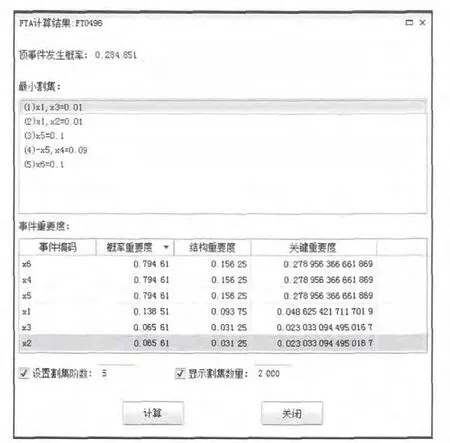
图3 CARMES 6.0的计算结果
3 结束语
本文提出一种基于模块化思想的复杂故障树重要度算法可在计算顶事件发生概率的同时获得各个模块中底事件的相对重要度,通过合并与递归计算即可得到所有的底事件在整个故障树中的重要度,与直接计算故障树重要度的方法相比,极大地提高了计算效率,尤其适用于规模较大的故障树分析。
[1]GJB/Z 768A-1998,故障树分析指南 [S].
[2]刘文彬.基于模块化思想的动态故障树分析方法研究[D].南京:南京理工大学,2009.
[3]张增照.故障树分析 [Z].广州:工业和信息化部电子第五研究所,2001.
[4]张超.基于BDD的动态故障树优化分析研究 [D].西安:西北工业大学,2004.
[5]李彦锋.复杂系统动态故障树分析的新方法及其应用研究 [D].西安:电子科技大学,2013.
