引导探究 做到“四引”

徐宏臻

随着课程改革的不断深入，现在，人们普遍重视探究，重视让学生经历“再探究”的过程，课堂面貌发生了可喜的变化。但综观一些探究活动，却不够充分、深入、扎实和有效：或只让学生做“操作工”，未让学生自主探；或只让学生得到知识的表面，未让其触及知识的内核；或只引领学生“探”知识，未引领学生“悟”思想；或只让学生得到既有的知识，未引领其自主创新等。因此，引导学生探究需要把学生——

一、引向自探

学生是探究的主人。引导学生探究必须要引导其自主探究，也只有自主探究才能真正培养学生的探究能力。为此，教师要以所教学的数学知识为载体，着力培养学生的自主探究能力；要营造宽松的探究环境，充分相信学生的潜能，精心设计现实的、有意义的和富有挑战性的数学问题情境，放手让其独立思考，自主探究，真正参与数学概念的形成和建立过程、数学规律的归纳和总结过程、数学问题的分析和解决过程等；要给予学生充足的探究时空，让其以探究者的姿态出现，并在教师科学、适时和恰当的引导下充分进行“再探究”“再发现”。实践证明：多“逼一逼”学生，多让其“试一试”“跳一跳”，学生的自主意识就会“长一长”。

如教学“小数乘小数”前，鼓励学生自主用多种方法计算“0.6x0.2”，并说明理由。教师既没有给出具体的问题情境，也没有提供任何暗示，就是要“逼”其充分调动已有的知识和经验自主解决问题，以催生他们的自主意识。学生想出了多种不同的算法：1.情境法，即编一个用0.6x0.2计算的实际问题，如一个长方形的长是0.6米，宽是0.2米，面积是多少平方米？因为0.6米=6分米，0.2米=2分米，6x2=12（平方分米），12平方分米=0.12平方米，所以0.6x0.2=0.12。2.根据积的变化规律，把小数乘小数转化成整数乘整数，如用0.6x10=6，0.2x10=2，因为6x2=12，所以0.6x0.2=12÷100=0.12；或因为0.6x2=1.2.2÷10=0.2，所以0.6x0.2=1.2÷10=0.12；或0.6x0.2=.（0.6x10）×（0.2÷10）=6x0.02=0.12；3.画图法，根据小数的意义画出6/10，再把6/10平均分成10份，涂出这样的2份，相当于把“1”平均分成100份，涂出这样的12份，因为0.6x0.2=12/100，12/100=0.12，所以0.6×0.2=0.12（图略）。

在展示和交流时，学生鲜明地感到算法的多样性和灵活性。在此基础上，教师引领学生聚焦：这些方法有何共同点？学生发现都是把未知转化为已知，都是把小数乘小数转化成整数乘整数。他们充分感受到转化的价值，从而学会了联系已有的知识和经验自主解决问题的方法。

二、引向明理

引导学生探究需要引导其探明道理，注重对知识本质的理解。新课标指出：“学生掌握数学知识，不能依赖死记硬背，而应以理解为基础，并在知识的应用中不断巩固和深化。”为此，教师不但要让学生探得知识“是什么”，而且要探明“为什么”“还可以是什么”“知识间的联系是什么”等，使学生达到实质性的、真正的理解。

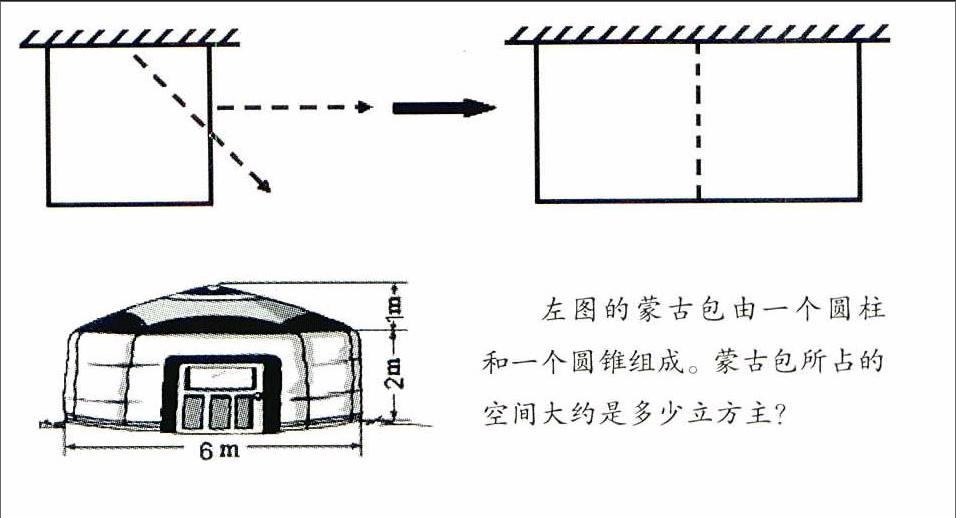
如复习“空间与图形”时，教材中编排了这样一题：

教材让学生小组合作，通过把根数是4的倍数的1米长的木条“围一围”“算一算”，借助列表和一一列举逐步感知规律，即当围成的长方形的长是宽的2倍时，面积最大。然而，探究不能到此为止，教师还应引领学生深入思考：为什么会有这一规律？它与以前的知识有何联系？如果木条的根数不是4的倍数还有这个规律吗？从中还能发现什么……

学生独立思考后，讨论交流，终于探明了原因：以前，在没有围墙时，用同样长的木条分别围成长方形和正方形，正方形的面积最大。现在“靠一面墙围”，就把原来正方形的一条边用一面墙代替，把节省下来的木条移到对边，并拼接起来，相应地把一条宽向右平移，就闻成了一个新的长方形。这个新长方形的长必定是宽的2倍。（如下图）