留数定理在积分计算中的应用

智丽丽 李艳青

（1，2.昌吉学院物理系 新疆 昌吉 831100）

积分计算不仅是高等数学的一大内容，也是其它学科在解决实际问题时需要处理的一大问题。针对各类不同形式的被积函数，往往难于求出其原函数，复变函数为我们提供了一个很重要的理论计算方法，即留数定理。

留数理论是复变函数论中一个重要的理论,尤其对于难于用解析方法求解的部分实变函数，可将实变函数转化为复变函数，借助留数定理得以求解，这样不仅可以使问题解决，而且，整个计算过程易于理解。利用留数定理进行积分计算的基本思想是：首先，将实变函数化为复变函数沿闭合回路曲线的积分，接着，将问题转化为求解闭合回路内部各个孤立奇点处的留数值，最后，利用留数定理得到被积函数的解。本文拟对留数定理做系统的归纳和总结，进一步认识这一重要定理在积分计算中的应用。

1 留数定理

设函数f(z)在回路l所围区域B上除有限个孤立奇点b1,b2,...,bn外解析，在闭区域B上除b1,b2,...bn外连续，则

显然，留数定理将回路积分归结为被积函数在回路所围区域上各奇点的留数之和。

2 留数定理在实变函数积分中的应用及例题分析

2.1 计算类型的积分

令z=eiθ，则有，从而将三角积分转化为复函数的回路积分：

2.2 计算类型的积分，积分区间是(-∞,+∞)

如果复变函数 f(z)在实轴上没有奇点，在上半平面除有限个奇点外是解析的，当z在上半平面及实轴上→∞时，zf(z)一致地→0。如果 f(z)是有理分式ϕ(x)/ψ(x)，上述条件意味着ψ(x)没有实的零点，ψ(x)的次数至少高于ϕ(x)两次。

这一积分通常理解为下列极限：

此时，构建一个半圆形回路l

根据留数定理，上式即：

令R→∞，上式左边趋于2πi｛f()z在上半平面所有奇点的留数之和｝，右边第一个积分趋于所求的定积分，第二个积分是趋于零的。

证明如下：

2.3 计算类型的积分

如果偶函数F(z)和奇函数G(z)在实轴上没有奇点，在上半平面除有限个奇点外是解析的；当z在上半平面或实轴上→∞时，F(z)及G(z)一致地→0。

首先，将所求积分的形式变换一下，

在右边的第二个积分中作代换x=-y，并考虑到F(x)是偶函数，得：

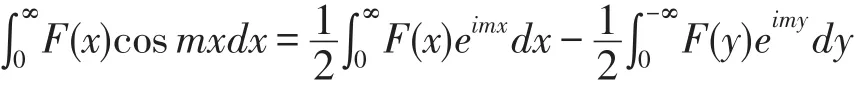
将右边第二项的积分变数再改为x，积分区间上下调换，前面成“+”号，则

利用留数定理得到:

3 总结

留数理论是复变函数论中一个重要的理论,借助该理论可以有效求解一系列实变函数的积分问题，解题思路清晰，便于理解和掌握，本文有助于定积分计算思路的扩展，促进实际问题中积分计算的高效求解。