基于多空间混合约束的NAO机器人抓取轨迹规划

王秋玥，方明，张海涛

（长春理工大学 计算机科学技术学院，长春 130022）

机器人手臂轨迹规划是当今服务控制领域研究的热点。针对机器人轨迹规划方法可以在笛卡尔空间和在关节空间进行，在笛卡尔空间使用逆运动学求解直接控制NAO机器人的末端效应器［1］。此空间的轨迹规划比较直观，但是由于冗余运动，规划过程中容易使机器人产出奇异位形；关节空间直接控制各个关节的角度，能保证运动路径的唯一性，但计算量很大，导致控制时间延长，并且末端效应器的运动轨迹不直观［2-4］。

本文提出用笛卡儿空间和关节空间相结合控制方法进行轨迹规划。在抓取目标大小已知条件下，利用关节空间控制方法预先设定各个关节的抓取角度，保证手臂抓取的最佳姿态，再用笛卡儿空间控制方法进行轨迹插值从而抓取目标。

1 混合空间描述

1.1 笛卡儿空间位置控制

在笛卡尔坐标空间中进行轨迹规划是指将手部的姿态表示成时间的函数，相应的关节位移、速度和加速度由手部的信息导出［5］。笛卡儿空间对NAO机器人进行控制使用NAOqi中API函数（如position-Interpolation（）是专门用来在笛卡尔空间中使用逆运动学求解直接控制NAO机器人的效应器。）效应器在NAO机器人中提前预定义三维点产生在生成链的尾部，如图1所示，根据已知坐标点可以在不同的坐标系（NAO，WORLD，TORSO）下建立不同点的坐标，本文在NAO坐标系下建立。NAO坐标系原点：NAO机器人的两脚垂直平分线上，X轴正方向始终在NAO的前方，Y轴正方向在NAO的左方，Z轴正方向在NAO的上方。

图1 NAO的各个效应器的位置和原点坐标

为保证运动轨迹的确定性，需要计算出机器人末端效应器经过路径上各个点时相对于机器人基本位姿，这个过程就是笛卡尔空间中路径规划过程［5］。

1.2 关节空间位置控制

在关节空间中对机器人进行控制，利用视觉测量得到目标位姿求解关节角，利用开始时刻和运动停止时刻的角度作为边界条件，然后使用常见的差值函数对关键点进行函数拟合［5］。关节控制可以是一个关节、关节链、一组关节。如关节控制NAO机器人手臂各个关节名称和各个关节的坐标轴。NAO机器人手臂具有5个自由度，其结构如图2所示。肩膀处有俯仰和横滚两个自由度，肘部具有偏转和横滚两个自由度，腕部具有偏转一个自由度。除此之外，手爪具有张合一个自由度。

图2 LArm各个关节名称和坐标轴

1.3 手臂轨迹规划

手臂运动的轨迹是指机器人在运动过程中的位移、速度、加速度，而轨迹规划是根据任务的要求，计算出预期的运动轨迹［4］。轨迹规划是在关节或笛卡尔空间中，对已知关键点的边界条件进行插值，求取相应符合任务需求的运动方程。

2 多空间混合约束手臂规划算法

NAO机器人的轨迹规划可以在笛卡尔空间，使机器人在位姿空间简化了一个坐标点即机器人末端效应器的坐标点，但会产生歧义位形。也可以在关节空间进行轨迹规划，关节空间中利用逆运动学求取各个关节的角度，但是需要大量复杂的矩阵计算。

本文提出一种使用关节空间控制和笛卡儿空间控制相结合的算法，进行轨迹规划，从而使NAO机器人完成抓取任务。NAO机器人在手臂抓取的范围之内，初始为站立状态的手臂轨迹规划如图3所示。

图3 NAO坐标系下多空间混合约束算法描述

通过NAOqi API自带的getPosition（）函数可以确定LArm的末端效应器在NAO坐标系下的坐标，即确定点PS。

由于抓取目标大小已知，可以在关节空间中预先设定抓取目标姿态，即设定LArm手臂的各个角度。NAO机器人的手臂只有5个DOF，其中WristYaw对轨迹规划的影响很小可以忽略，因此可以使用4个DOF，定义一个确定手部位置和姿态［2］，即设定NAO机器人LArm中ShoulderPitch、ShoulderRoll、ElbowYaw、ElbowRoll各个关节的角度，通过使用NAO机器人LArm的D-H参数如表1所示，其中UALen（UpperArmLength）的值如图4所示。相应的变换矩阵如公式（1）所示，表示任意两个参考系可以用一定的齐次变换矩阵来描述，其中包括两个旋转矩阵、两个平移矩阵。根据D-H坐标系变换方法，将表1中参数分别代入公式（1）中，可以求得总的变换矩阵，这个过程叫做正运动学分析。如公式（2）所示，通过依次右乘四个矩阵就可以得到总的变换矩阵。

表1 NAO机器人左胳膊的D-H参数表

图4 NAO机器人左胳膊相关链接的信息

其中，dn表示连杆的偏移量，an表示两杆的长度，αn表示连杆旋转角度，θn表示旋转关节的角度。

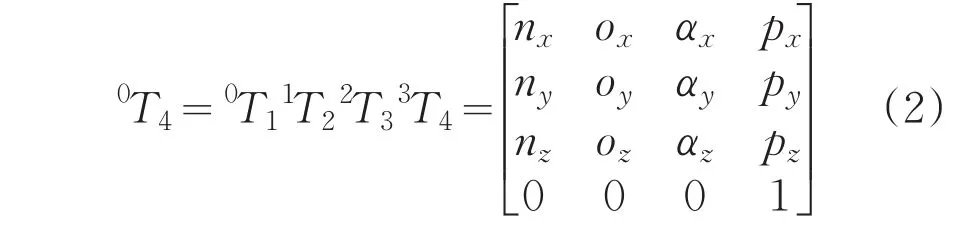
其中（px，py，pz）物体在基坐标系下的三维空间的坐标，（αx，αy，αz）方向为末端效应器进入刚体的方向为z向矢量又称接近矢量，（ox，oy，oz）指尖指向另一个指尖的方向为y方向矢量，称为方向矢量。（nx，ny，nz）方向为 x向矢量，称为法向矢量n，其中（nx，ny，nz）=（ox，oy，oz）*（αx，αy，αz），满足右手准则。

当机器人设定姿态后，其手部的姿态和位置也就确定，则可以在笛卡尔空间中进行轨迹插值［7］。

在笛卡尔空间中对PP和PG之间轨迹插值进行描述。由于NAO机器人手部坐标描述为6D（x,y,z，wx，wy，wz），其中手部姿态（wx，wy，wz）确定，因此只需考虑位置矢量（x,y,z）。既要保证NAO机器人抓取目标的最佳姿态，又要将手臂末端效应器移动到指定目标，很可能有一定的误差。即当机器人在空间中的姿态一定之后，机器人将不能再沿直线运动［8，9］。但是NAO机器人在设定姿态后，可以在一定范围内沿直线运动。给定抓取的目标具有一定的高度，Z轴的误差可以忽略，因此只考虑X，Y轴误差在1cm附近且NAO机器人手臂可抓取的范围内。将设定抓取位姿设置为坐标原点（0，0）。如图5所示，固定Y轴，得到X轴正方向移动最大的距离是6.5cm，此时X轴误差1.0cm，Y轴的误差0.4cm可忽略。X轴的负方向最大移动的距离是-5.5cm，此时X轴误差-0.001cm可忽略，Y轴误差-1.0cm。如图6所示，固定X轴，得到Y轴正方向移动最大的距离13.5cm此时Y轴误差1.15cm，X轴的误差0.6cm可忽略。Y轴负方向最大移动的距离是-0.13cm此时Y轴误差1.0cm，X轴的误差0.45cm可忽略。

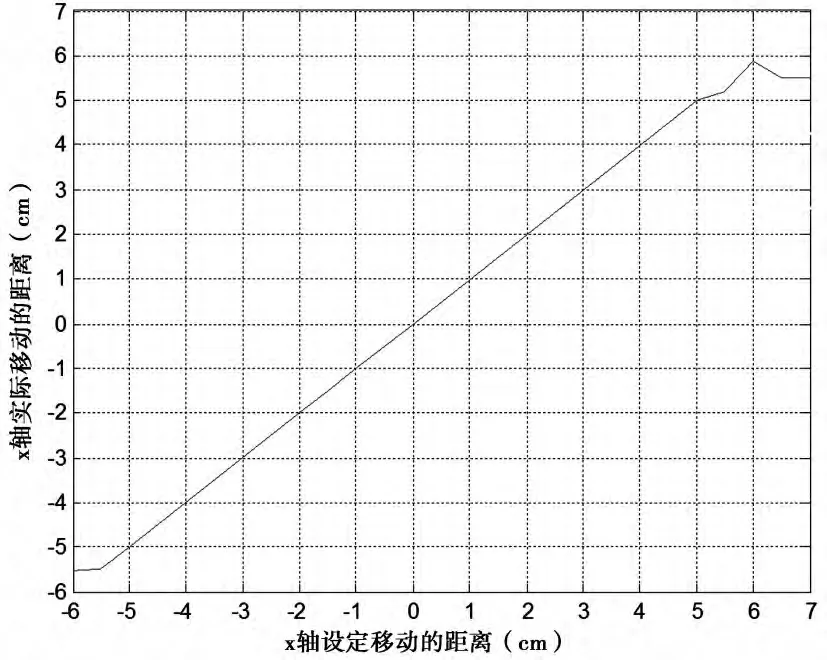
图5 设定姿态后X轴移动的误差范围

图6 设定姿态后Y轴移动的误差范围

故X轴，Y轴在设定姿态后抓取的范围：

手臂轨迹规划的伪代码如下所示：

（1）预先设定抓取目标的姿态；

（2）在关节空间中NAO坐标系下利用正向运动学获取手臂末端效应器移动点的坐标（x1，y1，z1）；

（3）设在NAO坐标系下目标点的坐标（xG，yG，zG），计算目标点与设定姿态点的相对坐标（xG-x1，yG-y1，zG-z1）；

（4）在笛卡尔空间中进行NAO坐标系下操作；

（5）分别在X，Y，Z轴上每隔2cm进行插值；

（6）逼近目标进行抓取。

3 实验

实验场景：NAO机器人抓取目标为红绿色柱。通过视觉测量得到在NAO坐标系下红绿色柱的坐标，确定红绿色柱坐标在手臂抓取范围内。NAO预先设定的姿态如图7（a）所示，通过NAOqi中API函数getPosition（）可知LArm的末端效应器的位置矢量坐标为（12.4379cm，13.0437cm，32.5971cm）。设定姿态后通过在笛卡尔坐标系下进行轨迹规划。NAO手臂移动的轨迹如图7（b）、（c）所示，最终抓取目标如图7（d）所示，实验结果如表2所示。

图7 基于混合空间NAO机器人手臂抓取过程

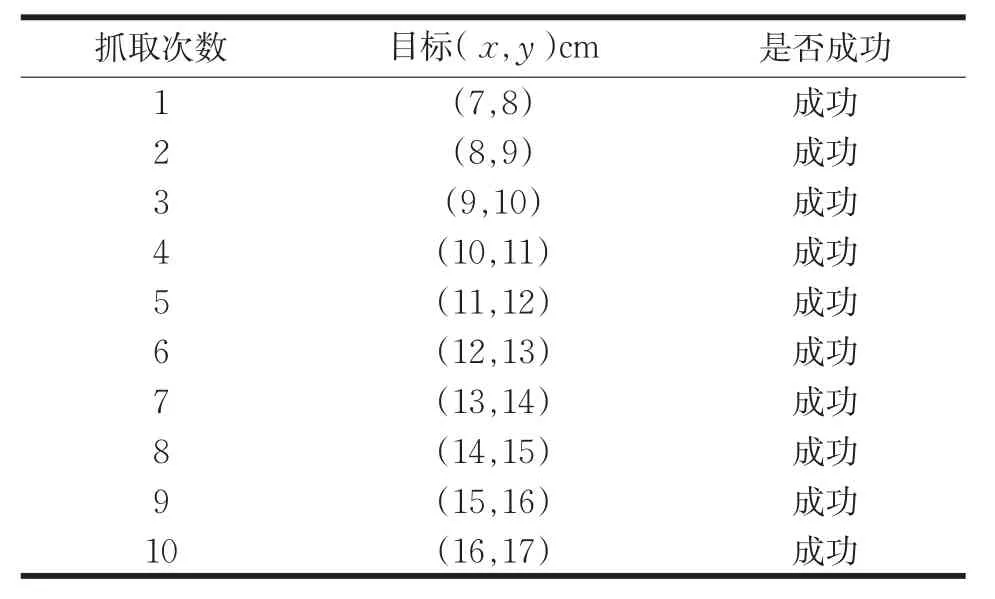
表2 多空间混合约束手臂轨迹规划实验

4 结论

本文提出对确定目标的前提下进行抓取的方法，既消除在笛卡儿空间中NAO机器人手臂出现冗余现象，又减少了在关节空间中计算各个关节角度的困难。实验表明，该方法在一定范围内进行轨迹规划目标抓取的方法是准确和可行的，计算量小而且容易实现。

［1］Louloudi A，Mosallam A，Marturi N，et al.Integration ofthe humanoid robotNao inside asmart home：A case study［C］.Proceedings of the Swedish AI Society Workshop（SAIS）.Linköping Electronic Conference Proceedings.2010，48：35-44.

［2］Muller J，Frese U，Rofer T.Grab a mug-object detection and grasp motion planning with the Nao robot［C］.Humanoid Robots（Humanoids），2012 12th IEEE-RAS InternationalConference on.IEEE，2012：349-356.

［3］任敬铁，孙汉旭.一种新颖的笛卡尔空间轨迹规划方法［J］.机器人学报，2002，24（3）：217-221.

［4］孙秀萍.机器人手臂规划的研究［J］.内蒙古师范大学学报：自然科学汉文版，2009，38（3）：174-177.

［5］程小宁.基于视觉反馈的机械手臂运动轨迹优化控制［D］.杭州：浙江大学，2007.

［6］杨贺然.基于机器视觉的移动目标机器人抓取研究［D］.北京：北京化工大学，2012.

［7］李光日，黄强，徐乾，等.小型防人机器人步态稳定控制方法研究［J］.长春理工大学学报：自然科学版，2014，37（3）：60-65.

［8］于清波.笛卡尔空间-五自由度机器人手臂自由度分析［J］.煤矿机械，2009，30（9）：113-114.

［9］熊家新，刘丽，徐鹤，等.全向轮式移动机器人的定位导航算法［J］.长春理工大学学报：自然科学版，2014，37（4）：83-88.